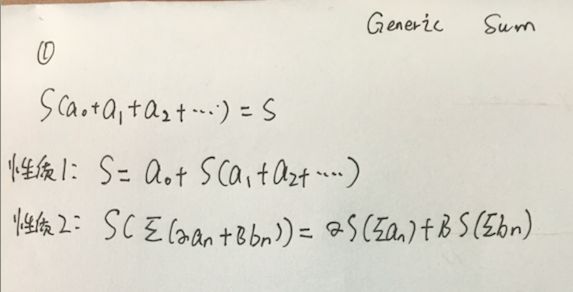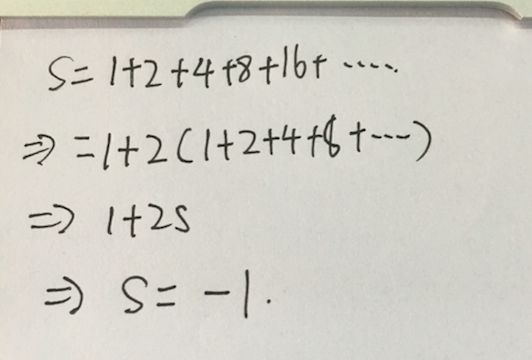大家好,这一篇文章是我在看完了网上的一个关于级数的证明之后,发现级数是如此神奇,在朋友圈分享了之后,引起了很多人的讨论,于是我想来探索下这个级数的定义,准备好,开动了:
说起级数,大家都并不陌生,在庄子里边就有一句话,叫做:一尺之锤,日取其半,万世不竭.说的就是有一根棍子,我们每一次都取一半,取一半的话,这个棍子永远都不会完结.其实这句话的结论就是1/2+1/4+1/8+......=1,这个结论我们在高中的时候就已经学过,但是如果我现在说:
1-1+1-1+1-1+…….. 这样的一个级数能不能求和,这时候可能有很多的同学就说,这个我知道,在高等数学里这个并不能求和,因为这不是一个收敛的级数,所以没办法求和.但是今天我要告诉大家,不是这样的,他不但可以求和,还可以得到一个有趣的数值”1/2”.同时我还要说,另外一个级数,跟他长得非常相似:”1+0-1+1+0-1+1+0-1+.........”他也是可以求和的,当然在高数里边我们也认为这是一个无法收敛的级数,那么他的和是多少呢?:”2/3”.看到这里,你是不是有点懵逼,你是在逗我吧.这两个级数长得几乎一模一样,我也没看出有啥区别,无非就是多了几个0而已,但事实上,他们的和是不一样的,而最重要的事情是他们都可以去求和.并且我还要告诉一个更加诡异的是:1+2+4+8+........这样的一个发散的级数,不但可以求和,还能够求出一个负数,这个答案是多少?”-1”,相信大家在得到这个结果的时候,大家三观都崩溃了.但是还有更有趣的哦,一定要坚持看完,我们之后还要把它证明出来.
还有一个更加有趣的事情:全体自然数之和:1+2+3+4+5+......全体加完,他的结果会是多少呢?”-1/12”.大家在这里可能听完就觉得我在胡说,一堆正数加起来怎么可能等于一个负数呢?而且跳跃级数怎么可以求和呢?这个在高数里边是严令禁止的东西,但是今天我们就用全新的方法去证明他,甚至还可以用物理实验来去证明他,这才是这篇文章最有意思的地方.
我们现在先来回忆一下刚才令人夸张的事实:一堆级数加起来会等于另外一个数,这时候我们想想有什么方法可以把他们加起来呢?在原来我们认为如果一个数越来越小的话,我们有可能是将其加起来成为一个固定的和的,但是每一项如果并不是无穷小,那怎么可以求和呢?这个时候我们就涉及到什么是和,什么是加法.
让我们来复习一下加法有什么定义:
1:加法是有交换律的
a+b=b+a
2:加法是有结合律的
a+b+c=(a+b)+c=a+(b+c)
3:加法是有分配律的
a(b+c)=ab+ac
那现在我们就用这三个加法的定律来去求证一下刚才那个非常奇怪的级数的和.我们就必须要去构建一下加法看起来非常重要的性质,因为我们可能已经发现,这三个定律已经没办法再去求我们这个级数的和了.那为什么不适合了么?比如说刚才的级数:1-1+1-1+1-1+.....如果此时我们认为加法的结合律和分配律依然存在的话,我们这时候如果把1(-1+1)(-1+1)+….把第二三项,四五项结合起来,这个时候就会结合出无穷个0来,这时候我们把无穷个0相加,再把最开始的1相加,他就会等于1,但是我们如果用结合律的方法的话,就会得出不同的值,我们换一种结合的方法(1-1)+(1-1)+......前两项相结合,又能够得到0+0+0+....这样的奇怪的组合,那最后的结果可能就是0,那现在我们就发现,如果我们用结合律的话,我们甚至可能连一个标准的值都得不到,这也就是为什么在高等数学里边我们无法对这样的跳跃的级数进行求和,因为他要求我们要有这样的一个加法的结合律,同时这时候加法的交换律也是无法保留的.不如让我们来看一个非常有趣的技术:1-1/2+1/3-1/4+........大家可以看到这是一个正负号一直在变换的级数,并且绝对值在不断变小,以前在高数里边我们知道这样的绝对值不断变小的级数是不能求和的,但是这个级数是非常幸运可以求和的,因为他等于ln(1+x)这样的一个函数在0点处的展开,这样就会变成:
所以我们很幸运的知道,这样的一个级数的和等于ln(2).
但是这样的一个级数,如果我们把结合律考虑进去的话,那其实可以得到我们任意想要的值.
比如现在我们要求π²用上边的级数,见证奇迹的时候到了:
很简单,我们只需要先把所有的正项数先加起来,也就是:
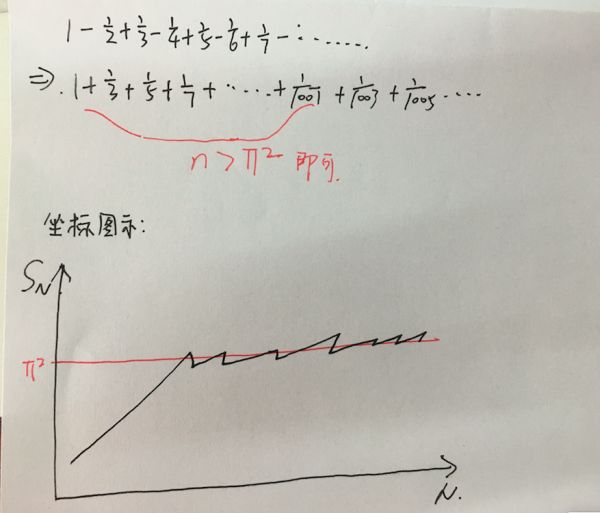
1+1/3+1/5+……
但是这样的级数是发散的,你总有加到某一项加到这一项的时候,这个全体的和会大于π²,这个是我们可以做得到的,一旦大于π²之后,我们再去加刚才我们故意略过的带负号的项数,比如先减去1/2,只要一减,就可以很快的让总的和小于π²,那一旦小于π²之后,我们又只取加的部分,比如刚才我们加到1/1001,突然减去1/2会小于π²,那么我们就再去加1/1003+1/1005+.....再去加无数多项,这样我们总是可以让其大于π²,那么一旦大于π²,我们就再去减,如此往复,我们会发现一个事情,如此往复的事情,其实就是把之前的数给换了一个加法的顺序,并且一个也没有落下,也就是说我们只要同时改变这样的加法的一个顺序,我们就会发现这样的一个级数和,画图来表示:
最后我们会发现他的振幅会越来越小,因为越往后绝对值的项数就越小,相应的振幅也就越小 .而这个就是高数对于我们的要求,如果他的振幅会随着n不断不断的变小的话,如果可以控制在一个极小的范围内的话,这就是他的极限.
所以我们就可以很果断说,如果我们可以控制他的项数,我们就可以控制到一个可以收敛的值.
那这样是不是就没得玩了,那如果我们愿意接受这样的交换律的话,其实这就是一场灾难,就已经没法用它去求无穷级数的和了.
所以到现在,我们还没有发现神奇级数应该如何的去求解,但是我们已经失去了一些工具,之前我们认为无比正确的加法的结合律和交换律在解决无穷级数的时候,已经失效了,那么最后留给我们的工具,就只有分配律了.那现在我们思考一下,那么为什么前两个可以抛弃,那分配律为什么要留下来?那是因为分配律是一个比原来的结合律基础的多的一个定律,它意味着加法还是保持有原来的一定的线性,这样的话我们就可以推导出前边好几类无穷级数的求和.
那不如就让我们立刻开始推导这样的无穷级数吧:
1:1-1+1-1+1……..
其实这个级数的求和,并不是我们第一次遇到,大数学家欧拉在18世纪的时候就已经遇到过了,那这个时候,欧拉提出了一个十分有趣并且有用的方法来计算这个级数的求和.
我知道这时候大家心里一定觉得不服,这跟我第一次知道这个事实感觉一样,为什么感觉欧拉这个级数是凑出来的,因为我们这个函数在-1点可能并不是收敛的,因此这样人觉得并不信服,所以一个世纪以后,法国的数学家波义耳又提出了一种计算刚才级数的方法,并且它的方法比欧拉的方法复杂的多得多
等于1/2这件事并不奇怪,真正奇怪的是欧拉算出是这个结果,一百年之后波义耳算出的用心的办法也是这个结果,这两个方法没有任何相似的地方,欧拉用的是一个简单的级数展开,波义耳用的是一个复杂的计算,但是都可以算出结果是1/2,那我们就很有可能认为1/2这个结果是正确的,那么这背后是不是还有更深层次的理论可以直接导出这个结果1/2呢?但是我们要发展一个理论,就要从最基础的东西去推导,刚才我们说过,加法交换律结合律已经在求无穷级数的时候失效了,那么这时候我们只有分配律,也就是刚才说的线性性.
那现在就让我们单纯的用线性性来推导出欧拉和波义耳的结论:1/2
如果能够从更基础的理论算出更简单的结果的话,这将成为更有力的武器,现在让我们介绍下Generic sum这个算法:
这里有两个性质:
上边这两条性质看起来是毋庸置疑的,那现在我们用这两条性质推出神奇级数的和:
那现在用这个定理得到的结果和之前欧拉推倒的和波义耳推导的得出的结论是完全一样的,其实更本质是,欧拉的算法和波义耳的算法都符合Generic sum算法的性质,另外都保留着线性性.
那现在我们再去思考一下:
1+0-1+1+0-1+1+0-1+……….这一个级数:
大家是不是会觉得,这个不就是上一个级数里边加了好几个0,他的结果应该不变.我们认为他的结果还是1/2,其实不对的,他的结果是2/3.究竟为什么是2/3.我们现在推到下:
那为什么这两个无穷级数如此像,但是一个却是1/2.另一个确实2/3?
难道无穷个0会改变数值么?其实就是这个样子的.接下来我们看看这个:
1+2+4+8+16+……
看到这个我们一定觉得高数白学了,这个在高数是绝对绝对不能求和的,但是如果我们认为他是可以求和的:
看到这里,有没有感觉整个人都不好了,一堆正数越加越大么不应该是,反而怎么会越加越小?
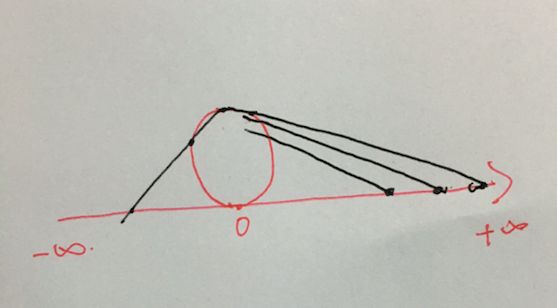
怎么理解呢?我们不如想一想复变函数中经常使用的函数说明:
我们认为从圆环上边的定点和实数轴上边的每一点连线都会有一个圆环的交点,当我们这样的数一直相加,数轴上的点其实是一直向右走,但是圆上的点会一直向上的,他有没有可能一直往上过头了会直接跑到左边去呢?成为一种负数呢?
这只是一种形象的方式,具体的计算还是需要Generic sum方法来计算,但是今天的终极大boss是全体自然数之和!
1+2+3+4+5+…….
这也可以求和!并且这样的求和是可以得到物理实验的验证的!
现在让我们来去求一下这样的级数求和,其实有点难,但是没有关系:
你是不是我在看玩笑,那我们用物理一个非常有趣的东西验证下:
我们在初中物理学到过,如果有两张纸片,中间吹一下,会得到两个纸片会靠到一起的结论,也就是说这两个纸片会有一种吸引力,初中我们会说这是伯努利效应,但是学过量子力学的我们,我们会认为两张纸之间会有一种卡西米尔力:
那这时候主要就是求集合n的值,如果假设n是正的,大于0,这时候我们会发现随着两张纸的距离不断变小,这时候平板之中的真空的能量是不断变大的,也就意味着这两个纸之间是由斥力,那如果他们是相互吸引的话,那么就可以说n的集合是小于0的.而这样的实验在2001年,卡西米尔效应在意大利的帕希尔大学测得在两个平板越来越近会存在一个引力的,这个是非常符合我们的结论的,真实世界和理论世界总是这么接近的!