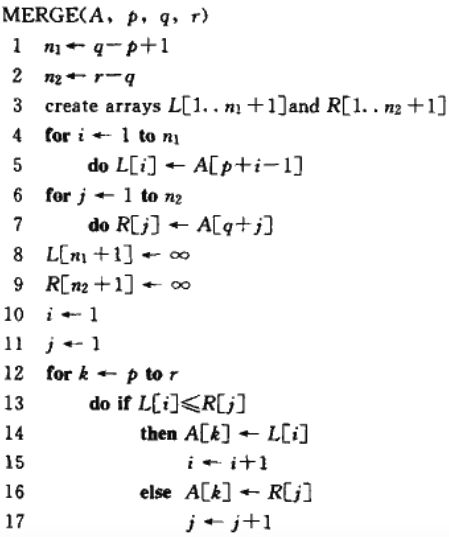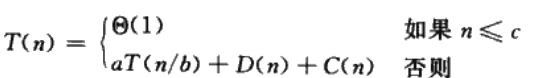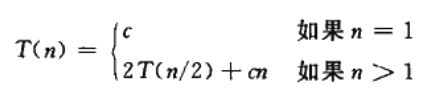版本记录
| 版本号 | 时间 |
|---|---|
| V1.0 | 2017.08.11 |
前言
将数据结构和算法比作计算机的基石毫不为过,追求程序的高效是每一个软件工程师的梦想。下面就是我对算法方面的基础知识理论与实践的总结。感兴趣的可以看上面几篇。
1. 算法简单学习(一)—— 前言
2. 算法简单学习(二)—— 一个简单的插入排序
算法设计
算法设计方法有很多,第二篇说的插入排序使用的是增量(incremental)方法,在排好子数组A[1 ... j - 1]后,将元素A[j]插入,形成排好序的子数组A[1 ... j]。
下面介绍另外一种算法的设计策略,分治法(divide - and - conquer)。
1. 分治法
很多算法在结构上是递归的:为解决一个给定的问题,算法要一次或多次地递归调用其自身来解决相关的子问题。这些算法通常采用分治策略,将原问题分成n个规模较小而结构与原问题相似的子问题;递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治模式在每一层递归上都有三个步骤:
- 分解
Divide:将原问题分解成一系列子问题。 - 解决
Conquer:递归的解各子问题,若子问题足够小,则直接求解。 - 合并
Combine:将子问题的结果合并成原问题的解。
2. 合并排序
合并排序(merge sort)算法完全按照上面的模式。
- 分解:将
n个元素分别各含有n / 2个元素的子序列。 - 解决:用合并排序法对两个子序列递归地排序。
- 合并:合并两个已排序的子序列以得到排序结果。
在对子序列排序时,其长度为1时递归结束,单个元素被视为是已排好序的。
合并排序的关键步骤在于合并步骤中的合并两个已排好序的序列,叫做合并。引入一辅助过程MERGE(A, p, q, r),其中A是一个数组,p, q, r是下标,且满足p ≤ q ≤ r,这里还假设A[p, q]和A[q + 1, r]都已排好序,并将它们合并成一个已排好序的子数组代替当前的子数组A[p ... r]。
MERGE的过程时间代价为O(n),其中n = r - p + 1是待合并的元素个数。
算法原理
这里就举一个扑克牌的例子,假设有两堆牌面朝上放在桌子上,每一堆都是已排序的,最小的牌放在做上面,我们要做的就是将这两堆牌合并成一个排好序的输出堆,面朝下的放在桌子上,基本步骤就是包括在面朝上的两堆牌中,选取顶上两张中较小的一张,将其取出后面朝下的放在输出堆中,重复这个步骤,直到其中的一个输入堆中为空停止,这时把输入堆中余下的牌面朝下的放入输出堆中即可。我们只是查看并比较顶上的两张牌,至多进行n次的比较,合并排序时间为O(n)。
伪代码
在给出伪代码之前,需要做一个小的改动,按照上面的原理我们需要时刻监测几个输入堆中是否有一堆是空的,为了避免这种循环的检查,我们换一个思路,在每一堆的底部放上一张哨兵牌(sentinel card)。它包含了一个特殊的值,用∞作为哨兵值,哨兵值漏出来时,不可能是两张中的最小的值,直到另外一堆也出现了哨兵牌,一旦出现这种两张哨兵牌同时出现,说明两堆牌中哨兵牌以外的牌都已经完成了排序。执行步骤次数r - p + 1后,算法就可以停止了。
下面看一下合并排序的伪代码。
下面我们就详细的说明下其过程:
- 第 1 行 计算数组
A[p ... q]的长度n1。 - 第 2 行计算数组
A[q + 1 ... r]的长度n2。 - 第 3 行创建数组
L和R,长度分别为n1 + 1,n2 + 1。 - 第4 ~ 5行,利用for循环将数组
A[p ... q]复制到L[1 ... n1]中去。 - 第 6 ~ 7 行,利用for循环将数组
A[p + 1 ... r]复制到L[1 ... n2]中去。 - 第 8 ~ 9 将哨兵元素至于L 和 R数组的末尾。
- 第 10 ~ 17 行维护一个循环不变式,执行
r - p + 1个基本步骤。
下面我们看一下上面算法的时间复杂度,这里1 ~ 3行和 8 ~ 11行都是固定的,也就是说时间都是常量,不会因为数组元素的个数增加而增加。第 4 ~ 7行中的for循环所需要的时间为O(n1 + n2)= O(n),并且第12 ~ 17行for循环共有n轮迭代,每一轮迭代所需时间都是常量。
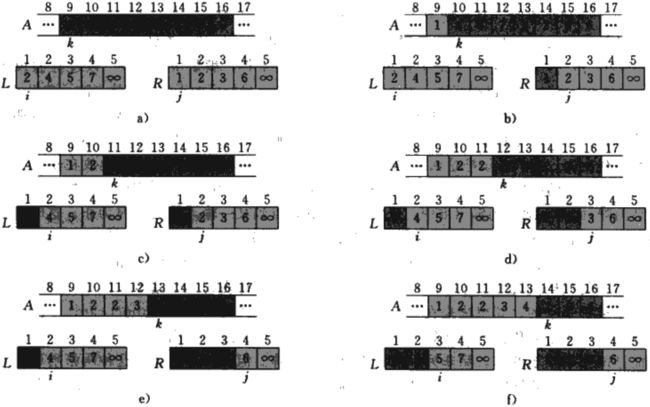
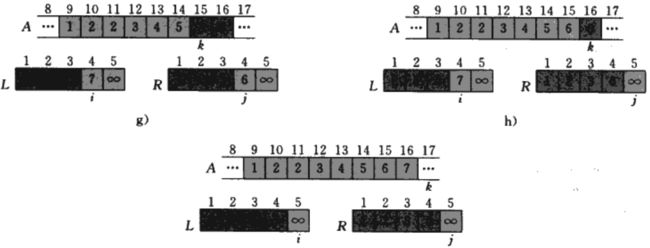
下面我们就以一个简单的例子看一下合并排序的步骤,先看下面两张图。
这里我们调用MERGE(A, 9, 12, 16)的第10 ~ 17行的操作中,当子数组A[9 ... 16]中包含序列{2, 4, 5, 7, 1, 2, 3,6}时的情况,在复制和插入哨兵后,数组L包含了{2, 4,5,7,∞},数组R包含了{1,2,3,6,∞},A中的阴影位置包含了它们的最终值,A中的浅阴影位置包含了它们的最终值。
循环不变式的验证
下面我们就验证12 ~ 17行循环不变式。在第 12 ~ 17 行中for循环每一轮迭代开始,子数组A[p ... k - 1]包含了L[1, n1 + 1]和R[1, n2 + 1]中的 k - p个最小的元素,并且是排好序的。
初始化:在for循环开始的时候,有
k = p,因而子数组A[p ... k - 1]是空的,这时i = j = 1,则L[i]和R[j]都是各自所在数组中,尚未被复制回数组A中的最小元素。保持:为了说明每一轮迭代都能使循环不变式成立,首先假设
L[i] ≤ R[j],那么L[i]就是未被复制回数组A中的最小元素,由于A[p ... k - 1]包含了k - p个最小的元素,因此,第14行将A[i]复制到A[k]后,子数组A[p ... k]将包含k - p + 1个最小的元素,增加k和i的值,会为下一轮迭代重新建立循环不变式的值,如果L[i] ≥ R[j],那么就会执行16 ~ 17行的代码,同样保持循环不变式成立。终止:在终止时,
k = r + 1,根据循环不变式,子数组A[p ... k - 1](此时即为A[p ... r])包含了L[1 ... n1 + 1]和R[1 ... n2 + 1]中k - p = r - p + 1个最小元素,已排好序。除了最大的两个哨兵元素,其他的元素都已经复制到数组A中。
详细分解过程
下面的过程MERGE - SORT(A, p, r)对子数组A[p ... r]进行排序,如果 p ≥ r,则子数组中至多只有一个元素,否则,分解步骤就计算出一个下标q,将A[p ... r]分成A[p ... q]和A[ q + 1 ... r],各自包含n/2个元素。抽象过程如下所示。
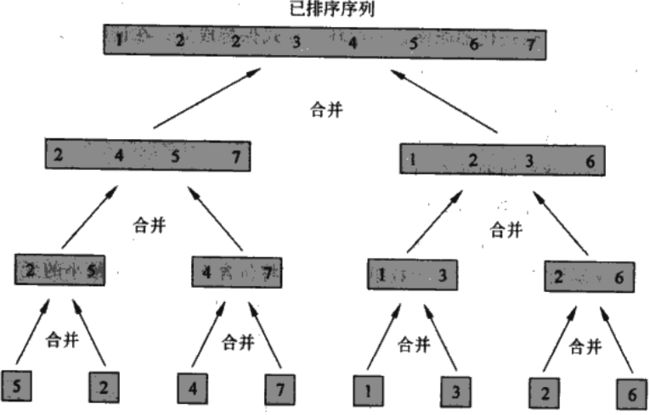
下面看一下数组A = {5, 2, 4, 7, 1, 3 ,2, 6}的合并排序过程。
分治法分析
当一个算法中含有对其自身的递归调用的时候,其运行时间可以用一个递归方程来表示,分治法递归式是基于基本模式中的三个步骤的。设T(n)为一个规模为n的问题的运行时间,如果规模很小,如n ≤ c, c为一常量,则得到直接解的时间为常量,写作O(1),假设我们把原问题分成a个子问题,每一个大小时原问题的1/b,如果分解该问题和合并解的时间各为D(n)和C(n),则有如下递归式。
合并算法时间消耗分析
有了上面时间消耗的表达式,我们其实可以根据主定理 (master theorem),可以证明T(n)= O(lgn),这里lgn就是以2为底的对数,这个增长速度要比线性增长的慢,因此,当n足够大的时候,合并排序最坏情况要比插入排序O(n^2)好很多。
时间消耗表达式可以简化为:
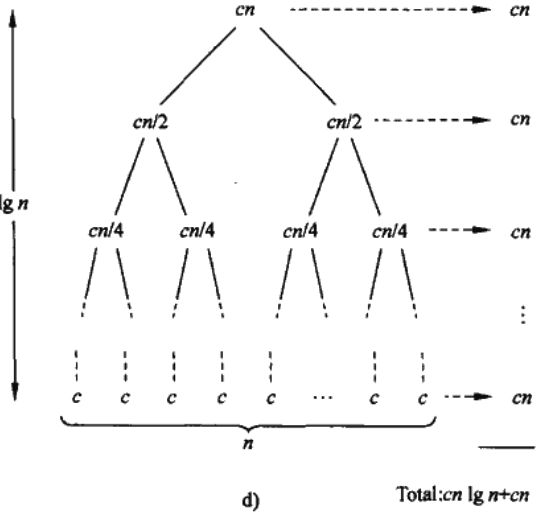
下面看一下上面时间消耗表达式所表示的递归树。
由上可知,总的表达式就是cnlgn + cn,也就是O(nlgn)。
代码验证
下面我们就看一下代码。
#include
#include
#include
int main(int argc, const char * argv[])
{
int A[8] = {2, 4, 5, 7, 1, 2, 3, 6};
int n1 = 4;
int n2 = 4;
//哨兵
int c = UINT8_MAX;
//L和R两个数组
int L[5] = {0};
int R[5] = {0};
for (int i = 0; i < n1; i ++) {
L[i] = A[i];
}
L[4] = c;
for (int i = n1; i < 8; i ++) {
R[i - 4] = A[i];
}
R[4] = c;
int i = 0;
int j = 0;
int k = 0;
for (k = 0; k < 8; k ++) {
if (L[i] <= R[j]) {
A[k] = L[i];
i ++;
}
else {
A[k] = R[j];
j ++;
}
if (L[i] == c && R[j] == c) {
break;
}
}
for (int k = 0; k < 8; k++) {
printf("%d\n",A[k]);
}
}
下面看输出结果
1
2
2
3
4
5
6
7
Program ended with exit code: 0
后记
未完,待续~~