注:本文是在看了两篇大牛的博客后,通过整理供自己学习快速排序所做笔记,分享出来方便大家学习。如需进一步了解可以查看文中博客链接。
一. 快速排序是什么
快速排序是图灵奖得主C. A. R. Hoare(1934--)于1960时提出来的。
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一不部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
整个排序过程只需要三步:
(1)在数据集之中,选择一个元素作为"基准"(pivot)。
(2)所有小于"基准"的元素,都移到"基准"的左边;所有大于"基准"的元素,都移到"基准"的右边。
(3)对"基准"左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
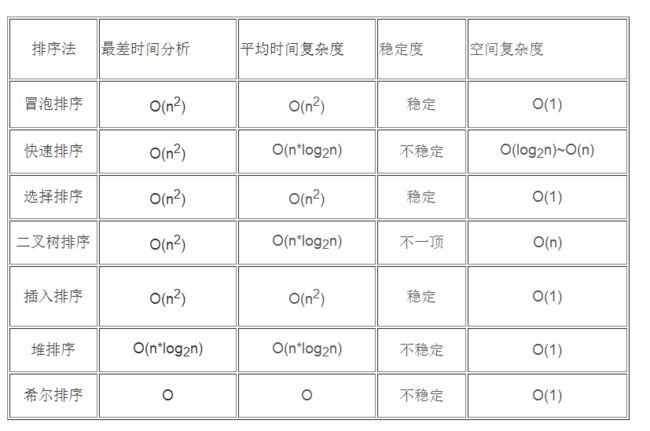
二. 快速排序的时间复杂度
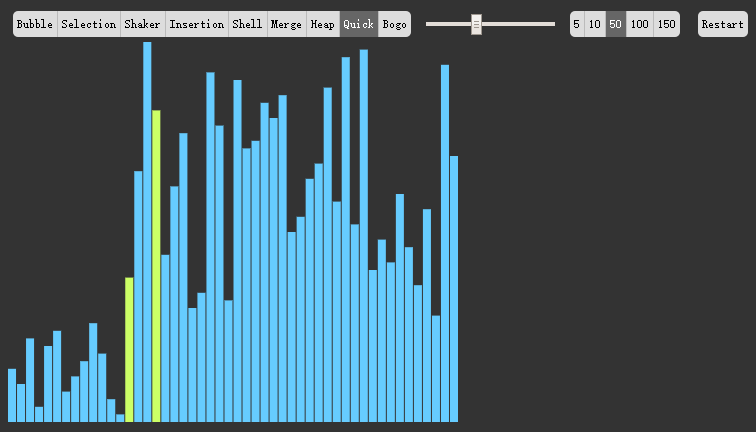
日本程序员norahiko,写了一个排序算法的动画演示,可以直观地将快排和其他排序方法的速度进行对比。
三. 快速排序为什么那么快
根据刘伟鹏的数学之美番外篇:快排为什么那样快一文所述,快排的本质上是一种通过问问题来缩小结果的可能性区间的策略。
下面我们将从最基本的猜数字和称小球讲起,总结其中蕴含的规律,然后一步步引申到排序问题上去。
1. 猜数字
假设有一个164之间的数,你来猜(你只能问答案是“是”或“否”的问题)。为了保证不论在什么情况下都能以尽量少的次数猜中,你应该采取什么策略呢?很显然,二分。先是猜是不是位于132之间,排除掉一半可能性,然后对区间继续二分。这种策略能够保证无论数字怎么跟你捉迷藏,都能在log_2{n}次以内猜中。用算法的术语来说就是它的下界是最好的。
为什么这种策略具有最优下界?答案也很简单,这个策略是平衡的。反之如果策略不是平衡的,比如问是不是在110之间,那么一旦发现不是在110之间的话就会剩下比N/2更多的可能性需要去考察了。
这种策略的本质可以概括成“让未知世界无机可乘”。它是没有“弱点的”,答案的任何一个分支都是等概率的。反之,一旦某个分支蕴含的可能性更多,当情况落到那个分支上的时候你就郁闷了。比如猜数字游戏最糟糕的策略就是一个一个的猜:是1吗?是2吗?… 因为这种猜法最差的情况下需要64次才能猜对,下界非常糟糕。二分搜索为什么好,就是因为它每次都将可能性排除一半并且无论如何都能排除一半(它是最糟情况下表现最好的)。
2. 称小球
12个小球,其中有一个是坏球。有一架天平。需要你用最少的称次数来确定哪个小球是坏的并且它到底是轻还是重。这个问题是一道流传已久的智力题。
我们先回顾一下猜数字游戏。为了保证任何情况下以最少次数猜中,我们的策略是每次都排除恰好一半的可能性。类比到称球问题上:坏球可能是12个球中的任意一个,这就是12种可能性;而其中每种可能性下坏球可能轻也可能重。于是“坏球是哪个球,是轻是重”这个问题的答案就有12×2=24种可能性。现在我们用天平来称球,就等同于对这24种可能性发问,由于天平的输出结果有三种“平衡、左倾、右倾”,这就相当于我们的问题有三个答案,即可以将所有的可能性切成三份,根据猜数字游戏的启发,我们应当尽量让这三个分支概率均等,即平均切分所有的可能性为三等份。如此一来的话一次称量就可以将答案的可能性缩减为原来的1/3,三次就能缩减为1/27。而总共才有24种可能性,所以理论上是完全可以3次称出来的。
如何称的指导原则有了,构造一个称的策略就不是什么太困难的事情了。首先不妨解释一下为什么最直观的称法不是最优的——6、6称:在6、6称的时候,天平平衡的可能性是0,也就是说我们得到的信息量为零。刚才说了,最优策略应该使得天平三种状态的概率均等,这样才能三等分答案的所有可能性。
只要记着这样一个指导思想——你选择的称法必须使得当天平平衡的时候答案剩下的可能性和天平左倾(右倾)的时候答案剩下的可能性一样多。实际上,这等同于你得选择一种称法,使得天平输出三种结果的概率是均等的,因为天平输出某个结果的概率就等同于所有支持这个结果(左倾、右倾、平衡)的答案可能性的和,并且答案的每个可能性都是等概率的。
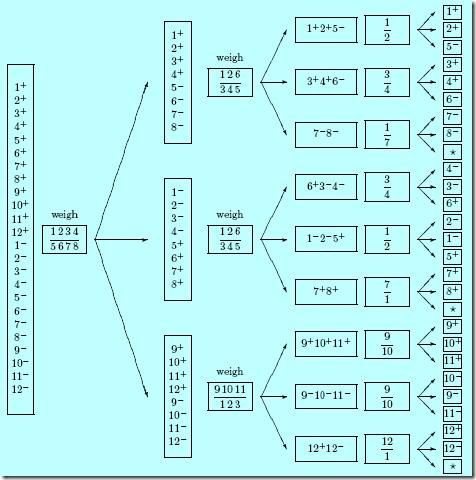
MacKay在他的书《Information Theory: Inference and Learning Algorithms》(作者开放免费电子书)里面4.1节专门讲了这个称球问题,还画了一张不错的图:
图中“1+”是指“1号小球为重”这一可能性。一开始一共有24种可能性。4、4称了之后不管哪种情况(分支),剩下来的可能性总是4种。这是一个完美的三分。然后对每个分支构造第二次称法,这里你只要稍加演算就可以发现,分支1上的第二次称法,即“1、2、6对3、4、5”这种称法,天平输出三种结果的可能性是均等的(严格来说是几乎均等)。这就是为什么这个称法能够在最坏的情况下也能表现最好的原因,没有哪个分支是它的弱点,它必然能将情况缩小到原来的1/3。
3. 排序(理想情况)
用前面的看问题视角,排序的本质可以这样来表述:一组未排序的N个数字,它们一共有N!种重排,其中只有一种排列是满足题意的(譬如从大到小排列)。换句话说,排序问题的可能性一共有N!种。任何基于比较的排序的基本操作单元都是“比较a和b”,这就相当于猜数字游戏里面的一个问句,显然这个问句的答案只能是“是”或“否”,一个只有两种输出的问题最多只能将可能性空间切成两半,根据上面的思路,最佳切法就是切成1/2和1/2。也就是说,我们希望在比较了a和b的大小关系之后,如果发现a
我们希望每次在比较a和b的时候,a
一个直接的推论是,如果每次都像上面这样的完美比较,那么N个元素的N!种可能排列只需要log_2{N!}就排查玩了,而log_2{N!}近似于NlogN。这正是快排的复杂度。
4. 排序(实际情况)
我们考虑快排的过程:随机选择一个元素做“轴元素”,将所有大于轴元素的移到左边,其余移到右边。根据这个过程,快排的第一次比较就是将一个元素和轴元素比较,这个时候显而易见的是,“大于”和“小于”的可能性各占一半。这是一次漂亮的比较。
然而,快排的第二次比较就不那么高明了:我们不妨令轴元素为pivot,第一次比较结果是a1 再进一步,如果第二步比较果真发现a2 这就是快排也不那么快的原因,因为它也没有做到每次比较都能将剩下的可能性砍掉一半。 将排序问题看成和猜数字一样,是通过问问题来缩小/排除(narrow down)结果的可能性区间,这样一来,就会发现,“最好的问题”就是那些能够均分所有可能性的问题,因为那样的话不管问题的答案如何,都能排除掉k-1/k(k为问题的答案有多少种输出——猜数字里面是2,称球里面是3)种可能性,而不均衡的问题总会有一个或一些答案分支排除掉的可能性要小于k-1/k。于是策略的下界就被拖累了。 知道了快排的思想与原理,下面我们就用javascript来具体实现一下快排。 首先,定义一个quickSort函数,它的参数是一个数组。 然后,检查数组的元素个数,如果小于等于1,就返回。 接着,选择"基准"(pivot),并将其与原数组分离,再定义两个空数组,用来存放一左一右的两个子集。 然后,开始遍历数组,小于"基准"的元素放入左边的子集,大于基准的元素放入右边的子集。 最后,使用递归不断重复这个过程,就可以得到排序后的数组。 使用的时候,直接调用quickSort()就行了。 参考来源:阮一峰、刘未鹏5. 小节
四. 快速排序的具体实现
var quickSort = function(arr) {
};
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
};
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2) ;
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
};
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2) ;
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
};
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};