Edit Distance编辑距离与动态规划

什么是编辑距离

编辑距离是指将一个字符串转化为另外一个字符串，需要的最少的编辑操作次数，这些操作包括增加、删除或者替换某个字符。可以看出，编辑距离越大，说明两个字符串的相似度越小；相反，编辑距离越小，说明这两个字符串的相似程度越大。两个字符串的编辑距离为0则说明这两个字符串相同。

计算编辑距离的方法

编辑距离的计算方式比较多，比较著名的有莱文斯坦距离（Levenshten distance）和最长公共子串长度（Longest common substring length）。

• 莱文斯坦距离允许的操作：增加、删除、替换字符三种编辑操作。表示的是两个字符串差异度大小。
• 最长公共子串长度的操作：只允许增加、删除字符这两个编辑操作。表示的是两个字符串相似度大小。

比如：字符串mitcmu和mtacnu的莱文斯坦距离是3，最长公共子串长度是4.

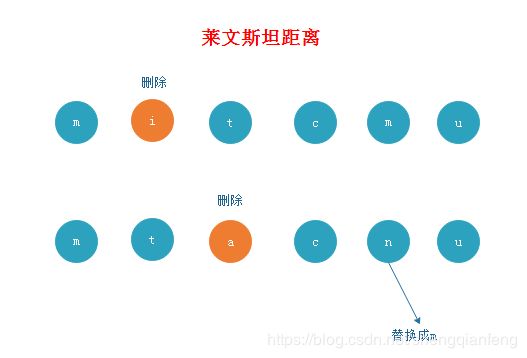
如何计算莱文斯坦距离

莱文斯坦距离就是找出两个字符串之间的差异度，即最小的编辑次数。

回溯思想计算莱文斯坦距离

这个问题其实可以使用回溯来解决，看你能否想到，思路如下：
依次考察一个字符串中的每个字符，跟另一个字符串中的字符是否匹配，比如a[i]和b[j]如果匹配，则继续考察a[i+1]和b[j+1].但如果a[i]和b[j]不匹配呢？如果不匹配，则有以下几种方式来处理：

• 可以删除a[i]，然后递归考察a[i+1]和b[i]
• 可以删除b[j],然后递归考察a[i]和b[j+1]
• 可以在a[i]前边添加一个跟b[j]相同的字符，然后递归考察a[i]和b[j+1]
• 可以在b[j]前边添加一个跟a[i]相同的字符，然后递归考察a[i+1]和b[j];
• 可以将a[i]替换成b[j]或者将b[j]替换成a[j],然后递归考察a[i+1]和b[j+1]

其实回溯计算的过程如果没有重复子问题则直接就用回溯就可以了，但是如果有较多的重复子问题动态规划则是更高效的方式。

DP思想计算莱文斯坦距离

DP思想解决问题的关键其实找到状态转移方式，而莱文斯坦距离的DP状态转移方式其实有三种，比如对于长度分别是n和m的字符数组a和b来说:

如果：a[i]!=b[j]，那么：min_edist(i, j) 就等于：
         min(min_edist(i-1,j)+1, min_edist(i,j-1)+1, min_edist(i-1,j-1)+1)
如果：a[i]==b[j]，那么：min_edist(i, j) 就等于：
         min(min_edist(i-1,j)+1, min_edist(i,j-1)+1，min_edist(i-1,j-1))
其中，min_edit(i,j)表示考察到a[i]和b[j]时经过的最小的编辑距离；min 表示求三数中的最小值。

试着理解下:
无论是min_edist(i-1,j)还是min_edist(i,j-1)，下一个状态如果是min_edist(i,j)必定是其中一个且仅是一个字符串往后移动了一个下标到达的min_edist(i,j)。这说明发生了编辑，编辑距离加一了。
当a[i]!=b[j]时, min_edist(i-1,j-1)需要加1容易理解因为a[i]和b[j]不等需要编辑。
当a[i]==b[j]时，min_edist(i-1,j-1)不需要加1，因为字符a[i]和b[j]相等不需要编辑。

这里有点难理解：
    min_edist(i,j-1)或者min_edist(i-1,j)转移到min_edist(i,j)应该加1，因为min_edist(i,j-1)或者min_edist(i-1,j)表示的是编辑距离，而编辑距离表示的是达到次数x时两个字符串相等。既然相等就肯定同时往后移动下标，所以不能简单理解为编辑距离，而应该思考min_edist(i-1,j)和min_edist(i,j)之间的状态转移关系。
    minDist[i-1][j]或minDist[i][j-1]到minDist[i][j]的转移，就是在字符串中增加了一个字符
比如hello和hllo，当i指向e，j指向l的时候，往hllo中加入字符e成为hello，那么此时j-1就是e，
j是l，就相当于是minDist[i][j-1]到minDist[i][j]的转移.
    于是he和hel的编辑距离minDist[i][j]为minDist[i][j-1]+1

动态规划计算公共子串长度

思路：
如果 a[i] 与 b[j] 互相匹配，我们将最大公共子串长长度加一，并且继续考察 a[i+1] 和 b[j+1]
如果 a[i] 与 b[j] 不匹配，最长公共子串长度不变，此时如下两种处理方式：

• 删除 a[i]，或者在 b[j] 前面加上一个字符 a[i].继续考察a[i+1]和b[j]
• 删除 b[j]，或者在 a[i] 前面加上一个字符 b[j].继续考察a[i]和b[j+1]

状态转移公式：

如果：a[i]==b[j]，那么：max_lcs(i, j) 就等于： max(max_lcs(i-1,j-1)+1, max_lcs(i-1, j), max_lcs(i, j-1))；

如果：a[i]!=b[j]，那么：max_lcs(i, j) 就等于： max(max_lcs(i-1,j-1), max_lcs(i-1, j), max_lcs(i, j-1))；

其中 max 表示求三数中的最大值。

代码实现

package com.study.algorithm.dp;

/**
 * @Auther: JeffSheng
 * @Date: 2019/10/21 16:02
 * @Description: 编辑距离的实现
 *
 */
public class EditDistance {

    private char[] a = "mitcmu".toCharArray();

    private char[] b = "mtacnu".toCharArray();

    private int n = 6;

    private int m = 6;
    /**
     * 存储结果
     */
    private int minDist = Integer.MAX_VALUE;

    /**
     *   回溯思想实现编辑距离
     *  调用方式 lwstBT(0, 0, 0);
      * @return
     */
    public void lwstBT(int i, int j, int edist) {
        if (i == n || j == m) {
            if (i < n){
                edist += (n-i);
            }
            if (j < m) {
                edist += (m - j);
            }
            if (edist < minDist) {
                minDist = edist;
            }
            return;
        }
        // 两个字符匹配
        if (a[i] == b[j]) {
            lwstBT(i+1, j+1, edist);
        } else { // 两个字符不匹配
            // 删除 a[i] 或者 b[j] 前添加一个字符
            lwstBT(i + 1, j, edist + 1);
            // 删除 b[j] 或者 a[i] 前添加一个字符
            lwstBT(i, j + 1, edist + 1);
            // 将 a[i] 和 b[j] 替换为相同字符
            lwstBT(i + 1, j + 1, edist + 1);
        }
    }

    /**
     * 动态规划思想解决编辑距离问题
     * 即由前一个状态决定后一个状态
     * @param a 字符数组a
     * @param n a的长度n
     * @param b 字符数组b
     * @param m b的长度m
     * @return
     */
    public int lwstDP(char[] a, int n, char[] b, int m) {
        int[][] minDist = new int[n][m];
        // 初始化第 0 行:a[0..0] 与 b[0..j] 的编辑距离
        for (int j = 0; j < m; ++j) {
            if (a[0] == b[j]){
                minDist[0][j] = j;
            }else if (j != 0){
                minDist[0][j] = minDist[0][j-1]+1;
            }else{
                minDist[0][j] = 1;
            }
        }
        // 初始化第 0 列:a[0..i] 与 b[0..0] 的编辑距离
        for (int i = 0; i < n; ++i) {
            if (a[i] == b[0]){
                minDist[i][0] = i;
            }
            else if (i != 0) {
                minDist[i][0] = minDist[i-1][0]+1;
            }
            else{
                minDist[i][0] = 1;
            }
        }
        // 按行填表
        for (int i = 1; i < n; ++i) {
            for (int j = 1; j < m; ++j) {
                if (a[i] == b[j]){
                    minDist[i][j] = min(
                            minDist[i-1][j]+1, minDist[i][j-1]+1, minDist[i-1][j-1]);
                }else {
                    minDist[i][j] = min(
                            minDist[i-1][j]+1, minDist[i][j-1]+1, minDist[i-1][j-1]+1);
                }
            }
        }
        return minDist[n-1][m-1];
    }

    private int min(int x, int y, int z) {
        int minv = Integer.MAX_VALUE;
        if (x < minv){
            minv = x;
        }
        if (y < minv){
            minv = y;
        }
        if (z < minv){
            minv = z;
        }
        return minv;
    }


    /**
     * 动态规划思想+最长公共子串长度法来计算编辑距离
     * @param a
     * @param n
     * @param b
     * @param m
     * @return
     */
    public int lcs(char[] a, int n, char[] b, int m) {
        int[][] maxlcs = new int[n][m];
        // 初始化第 0 行：a[0..0] 与 b[0..j] 的 maxlcs
        for (int j = 0; j < m; ++j) {
            if (a[0] == b[j]){
                maxlcs[0][j] = 1;
            }else if (j != 0) {
                maxlcs[0][j] = maxlcs[0][j-1];
            }else{
                maxlcs[0][j] = 0;
            }
        }
        // 初始化第 0 列：a[0..i] 与 b[0..0] 的 maxlcs
        for (int i = 0; i < n; ++i) {
            if (a[i] == b[0]){
                maxlcs[i][0] = 1;
            }else if (i != 0) {
                maxlcs[i][0] = maxlcs[i-1][0];
            }else{
                maxlcs[i][0] = 0;
            }
        }
        // 填表
        for (int i = 1; i < n; ++i) {
            for (int j = 1; j < m; ++j) {
                if (a[i] == b[j]){
                    /**
                     *  比如maxlcs[i-1][j]肯定是a[i-1]和b[j]不匹配，否则就是maxlcs[i][j+1]了，
                     *  所以说maxlcs[i-1][j], maxlcs[i][j-1]都不需要给公共长度加1，只有maxlcs[i-1][j-1]的a[i-1]和b[j-1]是相等的，i和j都同时加1
                     */
                    maxlcs[i][j] = max(
                            maxlcs[i-1][j], maxlcs[i][j-1], maxlcs[i-1][j-1]+1);
                }
                else{
                    //a[i]和b[j]既然不等，那么直接取前一个状态的最大值即可表示公共长度
                    maxlcs[i][j] = max(
                            maxlcs[i-1][j], maxlcs[i][j-1], maxlcs[i-1][j-1]);
                }
            }
        }
        return maxlcs[n-1][m-1];
    }

    private int max(int x, int y, int z) {
        int maxv = Integer.MIN_VALUE;
        if (x > maxv){
            maxv = x;
        }
        if (y > maxv){
            maxv = y;
        }
        if (z > maxv){
            maxv = z;
        }
        return maxv;
    }

    public static void main(String[] args) {
        EditDistance ed = new EditDistance();
        ed.lwstBT(0, 0, 0);
        System.out.println(ed.minDist);


    }

}