计算摄影：梯度域的图像处理

学过图像处理的人，对图像梯度的概念应该都不陌生，图像梯度，可以将一个图像值变成一个向量，如下图所示：

简单来说，就是对像素值，在 x, y 方向进行求导，从而可以得到图像在 x, y 方向的梯度，梯度域的图像处理，就是利用梯度的性质，对图像梯度进行计算，从而达到某些特定的效果，梯度域的图像处理最有名的就是泊松编辑，此外还有 tone-mapping， 图像拼接，图像融合等等，都可以用这种方法来实现。

在介绍梯度域的图像处理的原理之前，我们先来看看几个概念：
梯度，旋度，散度

• 梯度： 梯度的概念我们应该比较熟悉，梯度是一个向量，会指向变化最大的地方，而梯度大小，表示变化的幅度
• 散度： 散度的运算对象是向量，散度表示的是向量场中某个点的发散程度，是远离这个点，还是向这个点聚集
• 旋度： 旋度的运算对象也是向量，旋度表示的是向量场中，以某个点为中心，其周围点绕其旋转的程度。

旋度的表达：

$$Curl(▽I)=▽\times ▽I$$

散度的表达：

$$Div(▽I)=▽\cdot ▽I$$

对于图像来说，两者存在如下的关系：

在图像处理中，我们知道，$I_{xy}=I_{yx}$，因为图像的二阶导和求导顺序是没有关系的，所以图像梯度的旋度为 0，图像的二阶导一般都是用拉普拉斯算子实现。

梯度域的图像处理，一般来说，其 pipeline 如下：

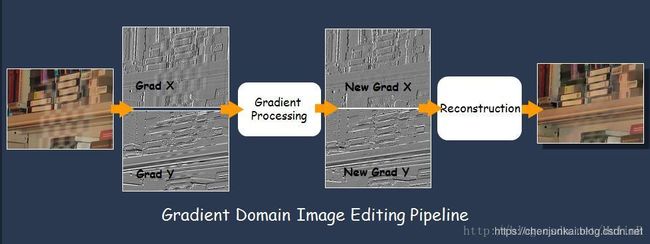
图片来源于： ICCV 2007 Course – Gradient Domain Manipulation Techniques

最困难的部分，应该是重建部分，假设我们要重建的图像为 $I$，其已知的梯度为 $\mathbf{v}$，那么我们主要就是要解决如下的优化方程：

$$\underset{f}{\min }{\iint }_{\Omega }|▽f-\mathbf{v}{|}^2$$

其中，$▽f$ 表示待求图像 $f$ 的梯度，$\mathbf{v}$ 表示已知的梯度，最后可以化简成求解如下的泊松方程：

$$\Delta f=\text{div}\mathbf{v}$$

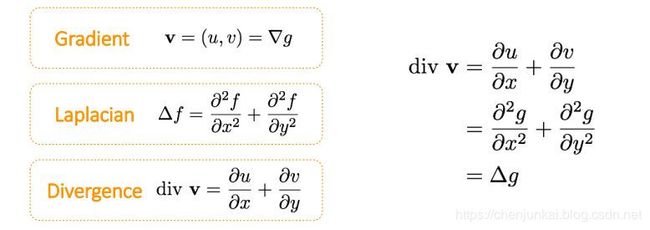
其中，$\Delta f$ 表示图像 $f$ 的二阶导数，$ \text{div} \mathbf{v}$ 表示已知梯度的散度，图像的二阶导数，可以用拉普拉斯算子来实现，上面的优化表达式意味着，希望待求图像 $f$ 的梯度和已知的梯度处处相等，所以有：

$$\Delta f_p=\Delta g_p$$

对于离散图像，一个像素点的二阶导，可以用拉普拉斯算子实现：

对应的 kernel 如下所示：

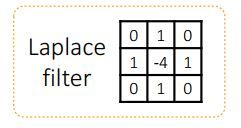
如果我们用一个稀疏矩阵来表示 拉普拉斯算子，那么可以得到如下的线性方程组：

$$\mathbf{A}\mathbf{x}=\mathbf{b}$$

其中，KaTeX parse error: Expected 'EOF', got '\mahtbf' at position 1: \̲m̲a̲h̲t̲b̲f̲{A} 是拉普拉斯算子组成的稀疏矩阵，$\mathbf{x}$ 表示要求的图像，被拉成了一维列向量，$\mathbf{b}$ 是已知的梯度的散度，拉成的一维向量，很显然，这是一个非常庞大的矩阵。

梯度，旋度，散度的概念参考了知乎上的解释：
https://www.zhihu.com/question/24074028/answer/26657334

参考文献： computational photograph, CMU 2018 lecture 10
参考文献： ICCV 2007 Course – Gradient Domain Manipulation Techniques
同样参考了：图像处理中的全局优化技术： https://blog.csdn.net/mulinb/article/details/9079645