基于自适应弹性网络回归的目标跟踪(OBJECT TRACKING WITH ADAPTIVE ELASTIC NET REGRESSION)阅读笔记

基于自适应弹性网络回归的目标跟踪(OBJECT TRACKING WITH ADAPTIVE ELASTIC NET REGRESSION)阅读笔记

by:家行hang
论文链接：
Object tracking with adaptive elastic net regression
Zhang, Shunli ; Xing, Weiwei
2017 IEEE International Conference on Image Processing, Sept. 2017, pp.2597-2601

参考：
1. 目标跟踪简介

摘要

近年来，各种基于回归的跟踪方法取得了很大的成功，然而，在大多数方法中，提取的所有特征都是用来表示对象的，而不需要进行特征选择。
(这里的意思是提取的所有特征全都用上了，而不是选择着去用)

本文提出了一种 基于自适应权（adaptive weight）弹性网络回归 的新的跟踪方法，一方面，跟踪被表述为一个 弹性网络回归 问题，它不仅可以充分利用空间信息，而且可以自动选择特征来减轻不稳定或不准确点的影响，另一方面，回归模型中的“1范数”和“2范数”正则化会自适应调整，以更好地提高性能。实验结果表明，所提出的自适应弹性网络回归跟踪方法能够获得满意的跟踪性能。

参考：
1. 机器学习中的正则化
2. 几种范数的简单介绍
3. 范数理解（0范数，1范数，2范数）
4. 【机器学习】正则化的线性回归 —— 岭回归与Lasso回归
5. 为什么正则化能减少模型过拟合程度
6. 为什么正则化（Regularization）可以减少过拟合风险

关键词：目标追踪，弹性网络回归（elastic net regression），自适应权（adaptive weight）

1 介绍

目标跟踪作为计算机视觉领域的研究热点之一，在视频监控、运动分析等领域有着广泛的应用。然而，跟踪面临着严重遮挡、变形、背景复杂等多种因素，难以实现鲁棒跟踪。

表观模型(appearance model)在跟踪中起着重要的作用，传统的表观模型一般可分为两类:
- 生成式模型（generative model）:就是只有一个模型，你把测试用例往里面一丢，label就出来了，如SVM。
- 判别式模型（discriminative model）:有多个模型(一般有多少类就有多少个)，你得把测试用例分别丢到各个模型里面，最后比较其结果，选择最优的作为label，如朴素贝叶斯。

（？？？表观模型中的区别呢？？？）

参考：
1. 产生式模型与判别式模型的区别
2. 机器学习–判别式模型与生成式模型
3. 生成式模型和判别式模型的区别
4. 机器学习 之 生成式模型 VS 判别式模型

近年来，一些基于回归的判别式模型取得了很大的发展，并获得了最先进的跟踪性能。例如,Hare等人提出了基于结构化输出回归的Struck方法，使用结构化输出预测来避免中间分类步骤,Henriques 等人提出了将跟踪表示为基于岭回归模型构造相关滤波器的问题，Zhang等人提出了基于混合支持向量机的跟踪方法，其中在目标的相邻样本基础上建立了支持向量回归模型。与传统的基于二分类的判别模型不同，回归模型具有一些明显的优势。例如，回归的目标和跟踪任务总是一致的，可以充分利用背景信息。然而，大多数基于回归的跟踪方法使用提取的所有特征。每个特性都被赋予相同的权重，并且不考虑特性的重要性。换句话说，就是没有特征选择。

在跟踪过程中，我们可以观察到目标的形状可能发生变形，或者目标发生了姿势的变化。此外，目标可能被另一个物体遮挡(Fig. 1).这些因素表明目标的某些部分不稳定，可能会影响表观模型的性能。遮挡也会干扰训练样本，从而降低模型的准确度。通过选取样本的稳定准确的部分建立外观模型，可以减少变形和遮挡的影响，提高鲁棒性。
（这部分说明特征选取的重要性，可以减少目标跟踪中变形和遮挡的影响。）

本文将跟踪问题表述为一个自适应弹性网络回归问题。弹性网络是一种包含 “1范数”和“2范数”正则化 的回归技术。它可以看作是 Lasso回归 和 岭回归 的结合，保留了上述两种回归模型的优点。弹性网络在许多领域都得到了应用，并取得了成功的应用。将跟踪定义为一个弹性网络回归问题可以带来两个好处：
- 弹性网络保持了回归模型的优点，可以利用背景的更多信息。
- 弹性网络能够自适应地选择稳定的特征进行训练，从而使表观模型更加精确。
　　

此外，我们提出了一种自适应策略来自动确定“1范数”和“2范数”的权重。实验结果表明，该方法可以获得与许多最先进的跟踪方法相似的跟踪结果。

2 用弹性网络回归跟踪

2.1 具有自适应弹性网络回归的表观模型

2.1.1 简述

虽然采用了岭回归和支持向量回归等不同的回归策略来构建回归表观模型，但权重向量w的正则项往往采用“2范数”，对特征的鲁棒性不够重视。在此，我们将跟踪定义为一个弹性网络回归问题，弹性网络能够自适应地选择最稳定的特征来学习函数，从而在“1范数”和“2范数”之间进行权衡，因此，我们使用弹性网来选择最鲁棒、最稳定的外观表现特征，减少变形、遮挡等因素对外观变化的影响。

具体来说，假设训练样本集为 x x ，其对应样本的元素为 xi x i ，回归值为 yi y i 。
线性回归函数可以定义为 f(x)=wTx f ( x ) = w T x ，其中训练样本 xi x i 和回归值 yi y i 均以相应的均值为中心。然后将弹性网络正则化回归的优化问题表示为:
　　　　　　　　 minw∑i12||wTxi−yi||22+λ(α1||w||1+α2||w||22),(1) m i n w ⁡ ∑ i 1 2 | | w T x i − y i | | 2 2 + λ ( α 1 | | w | | 1 + α 2 | | w | | 2 2 ) , ( 1 )
　　　　　　　　（？？？是加上了两种正则项的损失函数么？？？）
这里的 λ λ 表示误差与正则化之间的权衡参数， α1 α 1 , α2 α 2 控制“1范数”和“2范数”正则化的比例，并且 α1+α2=1 α 1 + α 2 = 1 。

此外，我们把等式(1)中的 α=[α1,α2]T α = [ α 1 , α 2 ] T 也视为优化参数。由于视频序列的不同帧中对象的稳定特性可能不同，不同视频序列中的对象也可能不同，因此对权衡参数进行自适应调整是有益的。
之后，等式(1)变为：
　　　　　　　　 minw,α∑i12||wTxi−yi||22+λ(α1||w||1+α2||w||22)+ρ2||α||22,(2) m i n w , α ⁡ ∑ i 1 2 | | w T x i − y i | | 2 2 + λ ( α 1 | | w | | 1 + α 2 | | w | | 2 2 ) + ρ 2 | | α | | 2 2 , ( 2 )
这里的 ρ ρ 也表示一个权衡参数，又加了一个新的正则化项 ||α||22 | | α | | 2 2 ，以便控制“1范数”和“2范数”的平衡。通过求解等式(2)中的优化问题，就可以用最优的 w w 和 α α 来表示外观模型。

2.1.2 优化（？？？）

由于有两个不同的参数 w w 和 α α ，等式(2)的优化问题可以通过两阶段迭代算法进行优化。首先，通过修正 α α ，等式(2)中的优化问题退化为等式(1)，等式(1)这是一个标准的弹性网络回归问题。目前已有很多现成的算法来解决在等式(1)中的优化问题。例如 LARS-EN 算法。在此，我们采用 SPAMS 工具箱来解决这个问题。
第二步，得到 w w 后，我们对其进行了修正并解决 α α 的优化问题：
　　　　　　　　 minw∑iλ(α1||w||1+α2||w||22)+ρ2||α||22,(3) m i n w ⁡ ∑ i λ ( α 1 | | w | | 1 + α 2 | | w | | 2 2 ) + ρ 2 | | α | | 2 2 , ( 3 )
这是一个二次优化问题，可以用Matlab直接求解。然后这两个步骤可以迭代进行得到最优的 w w 和 α α 。

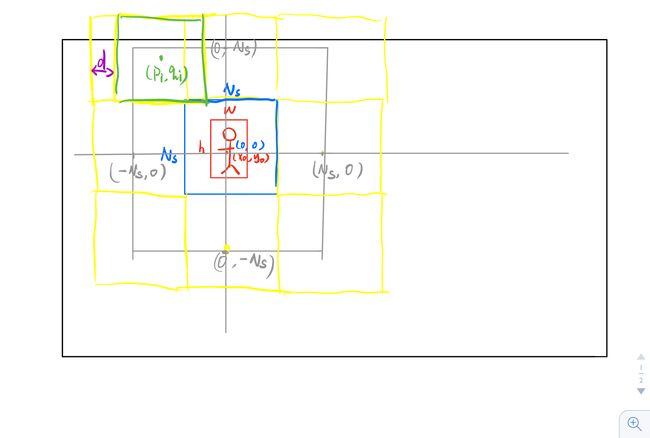
2.1.3 准备样本

基于滑动窗口策略，在网格中密集采样训练样本。假设目标中心的位置是 (x0,y0) ( x 0 , y 0 ) ,目标区域的宽度和高度分别为 w w 和 h h ,并且样本的归一化的大小是 NS× NS N S ×   N S ,此外，我们将归一化目标样本的坐标表示为 (0,0) ( 0 , 0 ) 。如果将训练样本按照归一化目标的像素密集采样，步长为 d d ，则归一化区域的训练半径为是 NS N S ，此外，我们希望训练样本能够覆盖不同程度的目标区域。因此，归一化样本 xi x i 在归一化区域中的位置就是 (pi,qi) ( p i , q i ) ,其中 pi,qi∈[−Ns,Ns] p i , q i ∈ [ − N s , N s ] 。相应地，归一化之前， xi x i 的位置为 (piw/Ns,qih/Ns) ( p i w / N s , q i h / N s ) (？？？为什么？？？)，这可以通过反向映射得到。通过在 [−Ns,Ns] [ − N s , N s ] 上改变 pi p i 和 qi q i ，我们可以得到所有与目标有不同重叠的训练样本。

参考：
1. 滑动窗口算法
2. 【深度学习理论】基于滑动窗口的目标检测算法

网格中选取的样本存储在相邻的缓冲区 Bn B n 中，提供了紧凑的空间约束。在我们的方法中， Bn B n 中的每个样本对应一个特定的位置。此外，我们还构建了另一个训练样本缓冲区，即深度为 D D （？？？）的目标缓冲区 Bt B t ，它由之前的跟踪结果填充，提供了时间约束。

2.1.4 确定回归值

为了使回归和跟踪的目标一致，在此，我们采用高斯函数作为回归函数，其中最大的回归函数值对应于目标的位置。由于我们将训练样本归一化到固定大小，所以可以通过归一化大小来实现高斯函数，以避免不同目标大小的影响。
　　　　　　　　 yi=exp(−(x¯¯¯(i)2+y¯¯¯(i)2)/σ2),(4) y i = e x p ⁡ ( − ( x ¯ ( i ) 2 + y ¯ ( i ) 2 ) / σ 2 ) , ( 4 )
x¯¯¯(i) x ¯ ( i ) 和 y¯¯¯(i) y ¯ ( i ) 分别表示样本 xi x i 的归一化相对水平和垂直位置, σ2 σ 2 表示高斯函数的方差。利用训练样本和确定的回归值，通过优化等式（1）中的问题，训练弹性网络回归模型，得到模型参数 w w 。

2.2 搜索策略

通过建立的表观模型，我们可以逐帧完成跟踪。在此，我们利用一个简单而有效的滑动窗口采样策略来寻找最优的跟踪结果。第 t−1 t − 1 帧获得的目标位置记为 lt−1 l t − 1 ,第 t t 帧的一个候选样本 xj x j 的位置记为 l(xj) l ( x j ) ,在第 t−1 t − 1 帧中我们在 lt−1 l t − 1 周围滑动采样窗口，获得一系列候选样本。如果 lt−1 l t − 1 和 l(xj) l ( x j ) 满足 ||l(xj)−lt−1||2<Rs | | l ( x j ) − l t − 1 | | 2 < R s , xj x j 将被选为候选样本。通过将候选样本归一化为固定大小并提取特征，通过计算得到候选样本 xj x j 的回归值 f(xj) f ( x j ) ， xj x j 的置信度可以表示为:
　　　　　　　　 conf(xj)=exp(−(f(xj)−ymax)2).(5) c o n f ( x j ) = e x p ⁡ ( − ( f ( x j ) − y m a x ) 2 ) . ( 5 )
然后，通过计算得到最优候选样本:
　　　　　　　　 xopt=argmaxxjconf(xj).(6) x o p t = a r g m a x x j ⁡ c o n f ( x j ) . ( 6 )
　　　　　　　　（arg代表当 conf(xj) c o n f ( x j ) 取最大值时，x的取值）

2.3 更新模型

在得到跟踪结果 xopt x o p t 后，我们更新弹性网络模型以适应外观的变化。为此，我们采用再训练策略（retraining strategy）来更新弹性网络模型。

由于我们已经将样本分为目标部分 Bt B t 和邻近部分 Bn B n ，我们分别更新 Bt B t 和 Bn B n 中的样本。对于 Bt B t ，我们以先入先出（First-In-First-Out(FIFO)）的原则更新样本，即最早进入目标缓冲区的样本将被 xopt x o p t 替换。对于 Bn B n ，由于每个位置对应的样本只有一个，所以我们选择与现有模型最小吻合的样本 Nu N u 进行更新。基于 xopt x o p t 的位置，我们首先根据章节2.1.3的介绍选择 xopt x o p t 周围的样本，然后通过回归模型来测量新样本与已有模型的吻合程度。假设新样本集为 X′ X ′ ，元素为 xi x i 。
对应 xi x i 的测度是 mi=|y^i−yi| m i = | y ^ i − y i | ,这里的 y^i y ^ i 为弹性网络模型对 xi x i 的预测值， yi y i 为预定义的理想回归值。 mi m i 值越大，说明样本 xi x i 不适合当前模型。
因此,我们选择 Nu N u 样本比其他样本更大，以 Bn B n 代替相邻位置相同的样本。利用更新后的样本，我们可以通过求解等式（1）来重新训练弹性网络模型，在提出的更新方案的基础上，可以对回归模型进行尽可能大的更新，以适应外观的变化。

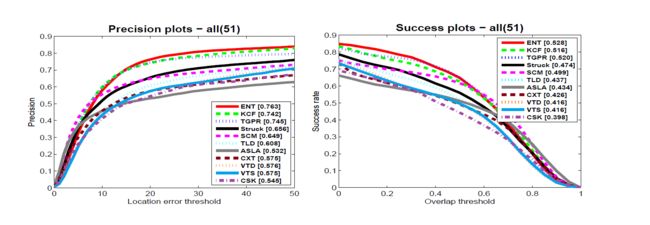
Fig.2. 上图是在所有51个序列的测试中，ENT和其他跟踪模型的精确图和成功图。方括号中的值分别表示精度图上 Thp=20 T h p = 20 像素处的精度和成功图上对应的AUC值。

Table 1. 下表是ENT和其他跟踪模型的CLE (in pixel), VOR,Precison 和 SR 的对比结果:

3 实验

3.1 初始化

提出的基于自适应弹性网络的跟踪方法记为ENT，初始化如下:
提取具有5像素窗口大小和9个方向的HOG特征来表示；
样本的归一化大小为 30× 30 30 ×   30 ；
训练半径和搜索半径分别设置为30像素和26像素；
高斯函数中， σ2=0.01 σ 2 = 0.01 ；
正则化参数中， α1 α 1 初始化为0.5， λ λ 初始化为0.5， ρ ρ 初始化为10;
为了更新的比值 Nu/M N u / M 初始化为0.05；
所有序列的参数都是固定的。（？？？这句话是什么意思？？？）

参考：
1. HOG特征（Histogram of Gradient）学习总结
2. 目标检测的图像特征提取之（一）HOG特征
3. 方向梯度直方图（HOG,Histogram of Gradient）学习笔记二 HOG正篇

3.2 与最先进的追踪器对比

3.3 参数分析

4. 结论

本文采用弹性网络回归方法构造了一种新的跟踪方法。将跟踪问题表述为弹性网络回归问题，既可以利用回归模型的优点，又可以利用弹性网络选择最稳定的特征进行表示。我们对基准数据集中的跟踪方法进行了评价，实验结果表明，该方法能比其他许多基于回归的跟踪方法取得更好的效果。