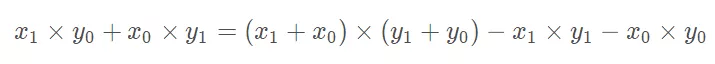计算机大数乘法引发的思考 | CSDN 博文精选
作者 | dog250
责编 | 屠敏
出品 | CSDN博客
近日,看了小小的一道学而思数学作业:
计算
201×33×707+484×636321×33×707+484×6363
我知道肯定是把数字拆开,配合结合律完成一种 “巧算” ,之所以称之为“巧算”,是因为这种算法比通过竖式直接硬算要节省不少步骤。
但我一下子想不到怎么拆解,我也懒得思考,因为我在思考另一件事。
上题的答案是(各种因数分解,结合律):
原式=67×3×33×707+11×44×9×707=67×3×33×707+11×44×9×707=11×99×707=111×99×7×101=777×9999=7770000−777=7769223
本文结束了,以下皆为附录。
1
通俗来讲,一个计算的所有步骤就是一个算法,算法的时间复杂度其实就是计算的规模和步骤数量之间的关系。
以乘法竖式为例,如果我们将一次十进制一位乘法(即99乘法表的乘法)作为一个步骤,那么两个n位乘数相乘需要n的二次方个步骤,其时间复杂度就是O(n
2) ,但是如果我们采用某种“巧算”,那么计算步骤将会大大减少。
小学,中学老师教的各种“巧算”技巧,其宗旨都是减少计算量。我们已经承蒙了12年有余的教诲,现在让我们进入计算机世界。
2
计算机乘法和我们用竖式计算乘法没有本质区别。看看加法器,乘法器的门电路就知道了。
门电路不是我们要关注的层次,门电路实在是太快了,快到你几乎无法感知它计算2×3和24890125×98723988的差别。机器是瞬间得到结果的。
人背下下来了99乘法表,所以人只能一位一位的计算乘法,但计算机不,计算机依靠自身的硬件门电路可以轻而易举计算出其内建数据类型乘法,64位的CPU可以轻易计算 0xFFFFFFFFFFFFFFFF 范围内的任意乘法,就好像我们人类计算99乘法表的乘法一样(我们早就把这个99乘法表背下来了,深刻在了我们的大脑硬件乘法器里)。
然而,超过计算机内建类型范围,计算机便无能为力了。
32位计算机最多只能处理32位的数字,64位计算机自然只能处理64位数字,计算机处理超过内建数据类型范围的数字计算的过程称为 “大数计算” 。
以64位为例,当计算机面对超过64位的数字乘法时,就好像我们人类面对超过一位数的乘法一样,无法 “一下子” 得到结果,必须需要某种步骤来计算结果。这就是说,需要某种算法来进行生成一系列的计算步骤,而 步骤的多少决定了算法的好坏。
举一个例子,我们尝试让计算机计算下面的式子:
23567971209865125789034451795247×12345678909988776655443314719047=?
我们当然希望设计一种巧算的步骤,但在此之前,我们先设计一种 按部就班的算法,类似我们手算竖式一样:
人就是这么算的,老老实实地按照十进制99乘法表,一个数字一个数字地进行计算,计算过程中处理进位。
手工算竖式人人都会,说这些也无益,上周三下班的班车上,顺手撸了一个代码,感觉还好,发了个朋友圈就想分享出来,本周就休息一天,赶早起来就写下了这篇文章。
模拟竖式计算的大数乘法C代码如下:
// mul.c
// gcc mul.c -o mul
#include
#include
#include
void inline carry_add(char *tmp, char num, int index)
{
char tmp_num = 0;
char carry;
tmp_num = tmp[index] + num;
if (tmp_num > 9) {
carry = tmp_num / 10;
tmp[index] = tmp_num%10;
carry_add(tmp, carry, index-1); // 递归进位到底
//tmp[index - 1] += carry; // 当次进位不能保证tmp[index - 1]+'0'是一个字符
} else {
tmp[index] = tmp_num;
}
}
int mul(char *mul1, char *mul2, char *result)
{
int i, j, mid;
int len1, len2, len, pos = 0;
char *tmp;
len1 = strlen(mul1);
len2 = strlen(mul2);
len = len1 + len2;
tmp = (char *)calloc(len, 1);
for (i = 0; i < len2; i++) {
for (j = 0; j < len1; j++) {
int idx = len - j - i - 1;
mid = (mul2[len2 - i - 1] - '0') * (mul1[len1 - j - 1] - '0');
// 这里我是在计算过程中直接递归处理进位的,而不是在一轮乘法后再用一个for循环处理。
carry_add(tmp, mid, idx);
}
// 我不需要在这里用for循环统一处理进位。
// Nothing todo!
}
i = 0;
while(tmp[i++] == 0) pos++;
len = len - pos;
memcpy(result, tmp + pos, len);
free (tmp);
for (i = 0; i < len; i++) {
result[i] += '0';
}
return 0;
}
int main(int argc, char **argv)
{
int len1, len2, i, count;
char *m1, *m2, *result;
m1 = argv[1];
m2 = argv[2];
count = atoi(argv[3]);
len1 = strlen(m1);
len2 = strlen(m2);
result = calloc(len1 + len2, 1);
// 为了比较速度,这里循环执行count次。
for (i = 0; i < count; i++) {
memset(result, 0, len1 + len2);
mul(m1, m2, result);
}
printf("%s\n", result);
free(result);
return 0;
} 大致就是这个意思。我们试一下这个程序:
[root@localhost ]# ./mul 23567971209865125789034451795247 12345678909988776655443314719047 1
290962605116854555936789385617202938185315195749798588574969609结果对不对开始我也不知道,不过从算法的执行过程上看,以一次简单乘法计数,这个算法的时间复杂度是O(n2)的,这种算法基本是要被毙掉的,所以必须进行优化。
哈哈,看到这里,可能很多人以为我要接着讲 Karatsuba乘法 以及 快速傅立叶变换了吧。
并不是,因为我不善于写教程,而且这方面的资源已经够多了,我再写一遍徒增冗余。我比较善于写一些思考的过程。
所以,我们按照相对常规的思路,循序渐进地来思考如何来优化程序。
记住,准则只有一个,即让计算的步骤变少!
看看上面的代码,算法完全模仿人类的手工竖式,按照十进制一位乘法来推进计算过程。但是这里面有个根本的问题,猜猜看是什么?
…
一位乘法对于人类而言是可以直接计算的,99乘法表都会背,我们计算4×7的时候,没有必要摆4排的7,然后数一数一共有多少,而是脱口而出28。对于人类而言,超过一位的数字乘法就属于大数了,人们不会把12×89这种计算的结果背下来,那就需要某种技巧去拆解多位数字,利用巧算来减少计算步骤了。
换句话说, 超过一位的十进制乘法计算,对于人类而言,就需要动用算法了。
然而,对于计算机却不是这样。
64位CPU可以直接计算 0xFFFFFFFFFFFFFFFF 范围内的乘法计算,就像我们计算乘法口诀里的乘法一样,脱口而出的那种。
这种能力是硬件门电路的可并发操作决定的,简单点说,64个引脚可以同时发射高电平或者低电平,但我们的人脑貌似只能同时发射一个十进制数字,这决定了计算机计算多位数字和我们对待99乘法表是一致的。
看看我们的一个优化思路:
对于计算机而言,没必要一位一位地计算啊,以64位机器而言,每次乘法计算的最大结果限制在 0xFFFFFFFFFFFFFFFF 就可以了。我们可以按照每8位一组来计算,因为保守计算, 99999999×99999999维持在 0xFFFFFFFFFFFFFFF 范围内。
好了,talk is cheap,下面是C代码( 这个算法很少见,一般人都是直接利用Karatsuba乘法的,几乎没有人利用这种思路来展示分治,所以,希望能仔细看看 ):
// mul2.c
// gcc mul2.c -o mul2
#include
#include
#include
void inline carry_add(char *tmp, char num, int index)
{
char tmp_num = 0;
char carry;
tmp_num = tmp[index] + num;
if (tmp_num > 9) {
carry = tmp_num / 10;
tmp[index] = tmp_num%10;
carry_add(tmp, carry, index-1);
} else {
tmp[index] = tmp_num;
}
}
// 处理大数加法
int add(char *s1, int len1, char *s2, int len2, char *result, int *ppos)
{
int i = 0, j = 0, len;
char *c;
len = len1;
if (len2 > len)
len = len2;
for (i = len - 1; i >= 0; i--) {
unsigned char tmp;
if (len1 > len2) {
tmp = s1[i] - '0';
if (i > len1 - len2 - 1)
tmp += s2[i - (len1 - len2)] - '0';
} else {
tmp = s2[i] - '0';
if (i > len2 - len1 - 1)
tmp += s1[i - (len2 - len1)] - '0';
}
carry_add(result, tmp, i + 1);
}
*ppos = 1;
if (result[0] != 0) {
len = len + 1;
*ppos = 0;
}
for (i = 0; i < len + 1; i++) {
result[i] += '0';
}
return len;
}
// 处理大数乘法
int zone_mul(char *mul1, char *mul2, int len, char *result, int result_len)
{
int i, j, n = 0, reslen, totlen, pow1size, pow2size, pos = 0, nblocks = len / 8;
unsigned long m1, m2, tmp_res;
char str1[10], str2[10], resstr[20];
char *pow1, *pow2, *tmp_result;
tmp_result = calloc(result_len, 1);
pow1 = calloc(len*2, 1);
pow2 = calloc(len*2, 1);
// 按照每8位十进制数字进行分割计算。
for (i = 0; i < nblocks; i++) {
memcpy(str1, mul1 + len - i*8 - 8, 8);
m1 = atoi(str1);
for (j = 0; j < nblocks; j++) {
memcpy(str2, mul2 + len - j*8 - 8, 8);
m2 = atoi(str2);
tmp_res = m1*m2;
// 计算补多少零,也就是乘以10的几次方
pow1size = i*8;
pow2size = j*8;
totlen = reslen = sprintf(resstr, "%lu", tmp_res);
totlen += pow2size;
memset(pow2, '0', totlen);
memcpy(pow2, resstr, reslen);
reslen = totlen;
totlen += pow1size;
memset(pow1, '0', totlen);
memcpy(pow1, pow2, reslen);
memset(result, 0, n + pos);
// 累加一次计算结果,执行大数加法
n = add(pow1, totlen, tmp_result, n, result, &pos);
memcpy(tmp_result, result + pos, n);
}
}
memset(result, 0, n + pos);
memcpy(result, tmp_result, n);
free(tmp_result);
free(pow1);
free(pow2);
}
int main(int argc, char **argv)
{
int len1, len2, i = 0, count;
char *m1, *m2, *result;
m1 = argv[1];
m2 = argv[2];
count = atoi(argv[3]);
len1 = strlen(m1);
len2 = strlen(m2);
result = calloc(len1 + len2, 1);
for (i = 0; i < count; i++) {
memset(result, 0, len1 + len2);
zone_mul(m1, m2, len1, result, len1 + len2);
}
printf("%s\n", result);
free(result);
return 0;
} 我们来比试一下效果,计算5000次同一个大数乘法:
[root@localhost ]# time ./mul 119334567890334449388883313579158334567098134455 667908995633221198765432134678040000123411113456 50000
79704631383957730438879843848804741889926116047138197998269353980447530720116354515911947726480
real 0m1.891s
user 0m1.889s
sys 0m0.001s
[root@localhost ]# time ./mul2 119334567890334449388883313579158334567098134455 667908995633221198765432134678040000123411113456 50000
79704631383957730438879843848804741889926116047138197998269353980447530720116354515912427726480
real 0m1.475s
user 0m1.472s
sys 0m0.001s
[root@localhost ]# 对于计算机而言, 用计算机力所能及的多位乘法代替人脑的一位乘法 会减少很多的计算步骤,多位乘法对于计算机而言并不苛刻,只要在它的内建支持范围内。就像我们计算99乘法一样,你不会觉得9×9 9\times 99×9比1×1 1\times 11×1更难。
3
但这个优化只是动用了计算机和人脑之间的能力差异,我们发明计算机就是让它来做计算的,这注定使得它不可能用人类的一位计算方式去做竖式。我的算法保守采用了8位十进制来计算,但这只是最基本的常识,并不算优化。
换句话说,这只是开始。
那么,接下来做什么?这才是该考虑的。
4
重新回想小小的学而思课后数学题:
201×33×707+484×6363
再想想如何来解题。诚然,任何人都知道需要巧算而不是硬算,所谓的巧算就是利用一些初等数学知识,比如将201分解成67和3的乘积或200和1的加和。
计算机能不能通过类似因式分解,拆项,结合律来优化计算步骤呢?
很遗憾,计算机没有智能,目前计算机的所有智能需要程序员来灌入。在将一些策略灌入计算机之前,程序员需要自己先把结果算出来,然后编程呗…
人可以先把通用公式做出来,然后编程套用即可。
5
现代数学异常强大,我们可以将一个数字:
进行如下分解:
我们知道,多项式有很多性质,如果我们能把一个任意数字表示成多项式,我们就可以利用这些性质了。
这个时候才是引出 Karatsuba算法 的最好时机。
任意两个数字x,y我们可以任意取数字m,然后将其表示为:
x*y都会算吧,结果就是:
巧吗?很遗憾,不巧,我们依然还是要处理:
以上的四次乘法,没有任何节省。
然而,如果继续化简,就会发现
之间是有关系的:
4个乘法减到了3个乘法,其中:
化成了两个加法和一个乘法,很不错。
计算机教科书上针对Karatsuba算法的常规描述是使用递归实现,递归的退出条件是乘数称为一位十进制数,这是大错特错!根本没有必要让乘数称为一位数时才退出递归,64位机器上两个乘数均是8位数字以内时就可以直接相乘而退出递归,让计算机去计算自己力所能及的最大计算量,岂不是最好?
Karatsuba乘法 没什么大不了的,无非就是利用人类的成果而已。这非常类似于一元二次方程的求解,人类去算的话,可以直接套用公式,而纯让计算机去解,只能一个一个数字去枚举尝试。
Karatsuba乘法我就不再说了。我说点别的。
如果仔细观察一个多位数字的多项式表示,我们可以利用的性质还有很多,即便是快速傅立叶变换,也不过是其中之一。这就是现代数学成果的展示和利用。
但是要知道,即便可以编程实现快速傅立叶变换来计算大数乘法,也只是利用了人类推导的结果,换句话说就是套公式,你并没有利用计算机的优势,而计算机的优势就是可以非常快速地一个一个试。
简单总结,如果你能把一个数字:
化为:
那么你就能利用一切关于多项式的直接结论去求解类似大数相乘的问题。这就好比说,让你求一个方程的解:
你可以利用计算机的快速计算能力一个一个数字的枚举,你也可以直接利用韦达定理,求根公式,但是要记住,这不是计算机的能力,这只是计算机程序表达公式的能力。
总而言之, 面对一个大数计算,手算情况下你觉得怎么操作方便,就把这种操作编程实现,这就是优化。
6
我们真的是细思极恐,我们的所谓现代密码学原来完全建立在 “现代计算机不是建立在2048位的基础之上的” 。
RSA密钥长度2048位已经被证明相当安全了,但是数学上可以证明的所谓难题如果面对真正的2048位计算机会怎么样…如果真的有2048位计算机,破解RSA还会很难吗?内建2048位的门电路引脚可以同时发射2048位的电平信号,可以预期可以瞬间分解2048位的密钥,这是多么恐怖的事情。
然而对于此类梦想,2048位计算机难呢,还是量子计算机难呢?经理说,筚路蓝缕,以启山林。
【这里需要订正一下关于上一段RSA的论述】:
并不是说有了2048位字长的计算机就可以暴力破解RSA了,而是说有了2048位字长的计算机之后,大数乘法的开销就被压缩了,按照nlogn倍压缩掉了。遍历2048位解空间的开销丝毫不受影响,受影响的只是拆解,计算2048位大数(2048位字长的计算机中不叫大数了…)的开销。
换句话说,RSA暴破难题包括两部分,一部分是数学上的,这是由数学决定的,另一部分是实现上的计算开销,这个开销受计算机结构,字长,时钟频率,算法等一系列因素影响,如果实现了2048位字长的计算机,这些开销将会大大降低,如果是量子计算机,2048位解空间可以并行开解,那就更快了,但是也丝毫没有动摇RSA算法的数学基础。
突然有人问我一个关于快速排序为什么快的问题,搜到之前自己的文章,有点想法。
有人问我在同样O(nlogn) 的时间复杂度情况下,为什么快速排序比归并排序快,我没有办法证明,但是事实上的原因却是非常显然的:
随机的就是最好的!
详见:
不知为不知–信息论和最大熵原则 :https://blog.csdn.net/dog250/article/details/78944526
版权声明:本文为CSDN博主「dog250」的原创文章。