234树

引入

       在二叉树中，每个节点有一个数据项，最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点，就是多叉树（multiway tree）。
       2-3-4树，就是多叉树，它的每个节点最多有四个子节点和三个数据项。首先，2-3-4树像红黑树一样是平衡树。它的效率比红黑树稍差，但是编程容易。

234树：

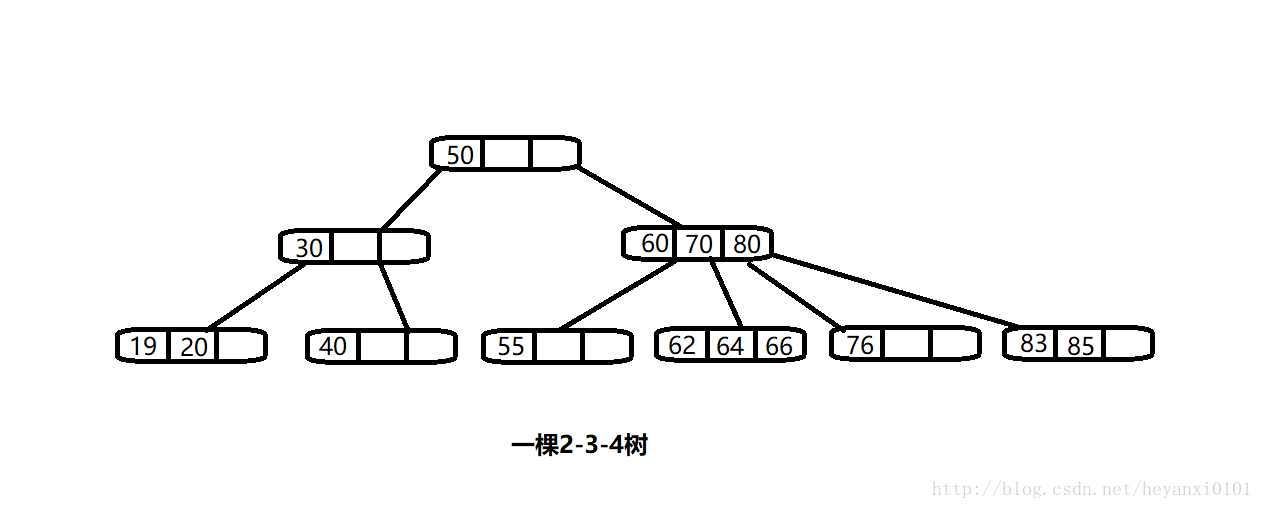
· 上图展示的就是一棵2-3-4树，每个节点可以保存一个、两个或者三个数据项。
· 上图中上面三个节点有子节点，底层的六个节点都是叶节点，没有子节点。2-3-4树中所有的叶节点都是在一层上的。

2-3-4树名字的含义：

2-3-4树中的2、3、4的含义指的是一个节点可能含有的子节点数。对非子叶节点有三种可能的情况：
       · 有一个数据项的节点总是有两个子节点
       · 有两个数据项的节点总是有三个子节点
       · 有三个数据项的节点重是有四个子节点
       上述的重要的关系决定了2-3-4树的结构，比较而言，叶节点没有子节点，然而他可能还有一个、两个、三个数据项。空节点是不会存在的。在2-3-4树中不允许只有一个连接。有一个数据项的节点必须总是保持两个连接，除非它是叶节点，在那种情况下没有连接。

2-3-4树的组织：

为了方便起见，用从 0 到 2 的数据给数据项编号，用 0 到 3 给子节点编号，从左到右升序。
       树结构中很重要的一点就是它的链与自己的数据项的关键字值之间的关系。2-3-4树中的规则和二叉树的规则大体一样，但是还加上了以下几点：下面的情况指的是有三个数据项且有四个子节点的情况：
       · 根是 child0 的子树的所有子节点的关键字值小于key0；
       · 根是 child1 的子树的所有子节点的关键字值大于key0并且小于key1；
       · 根是 child2 的子树的所有子节点的关键字值大于key1并且小于key2；
       · 根是 child3 的子树的所有子节点的关键字值大于key2。

搜索2-3-4树：

       查找特定的关键字值的数据项和在二叉树中的搜索例程很类似。从根开始，除非要查找的关键字值就是根，否则选择关键字值所在的合适范围，转向那个方向，知道找到为止。

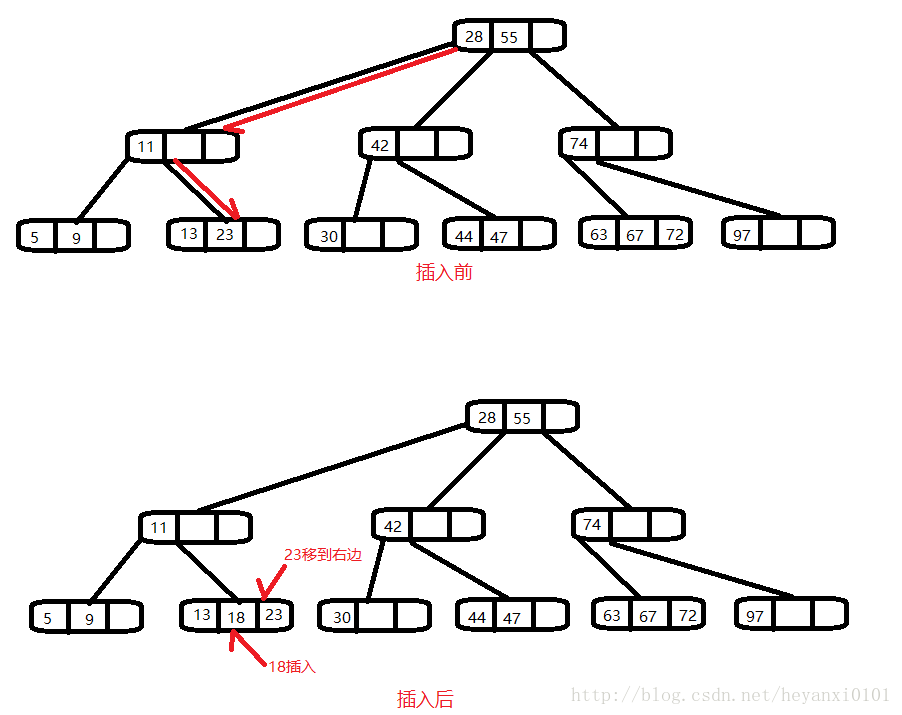
插入数据：

·新的数据项插入总是在叶节点里，在树的最底层。如果插入到有子节点的节点里，子节点的编号就要发生变·化以此来保持树的结构，这保证了节点的子节点比数据项多1。
**·**2-3-4树中插入节点有时比较简单，有时相当复杂，无论哪一种情况都是从查找适当的叶节点开始的。
·查找时没有碰到满节点时，插入很简单。找到合适的叶节点后，只要把新数据项插入进去就可以了。
·插入可能会涉及到在一个节点中移动一个或者两个其他的数据项，这样在新数据项插入后关键值仍保持正确的顺序。

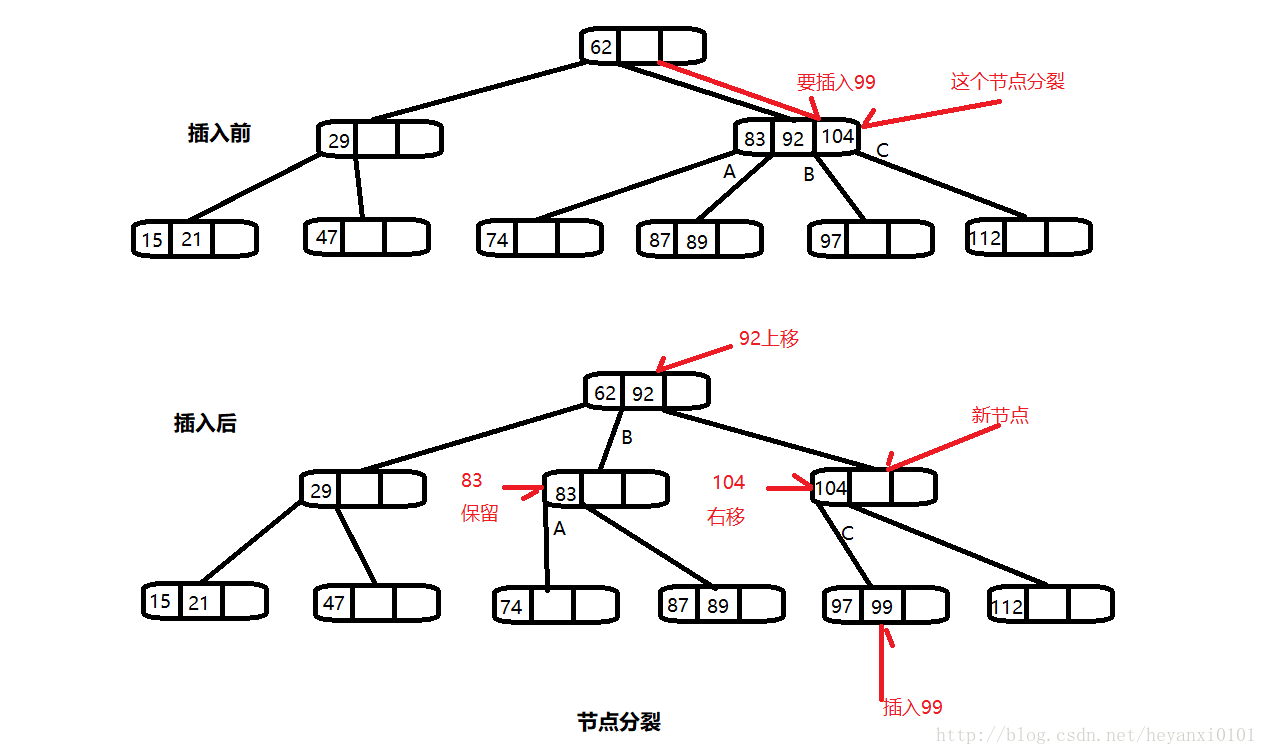
节点分裂：

       如果往下寻找要插入位置的路途中，节点已经满了，插入就变得复杂了。发生这种情况时，节点必须分裂，正是这种分裂的过程保证了树的平衡。
       把要分裂节点中的数据项设为A、B、C，下面时分裂时的情况。（假设要分裂的节点不是根）
要进行下面的步骤：
       · 创建一个新的空节点，它时要分裂节点的兄弟，在要分裂节点的右边
       · 数据项C移到新节点中
       · 数据项B移到要分裂节点的父节点中
       · 数据项A保留在原来的位置
       · 最右边的两个子节点从要分裂处断节点处断开，连到新节点上

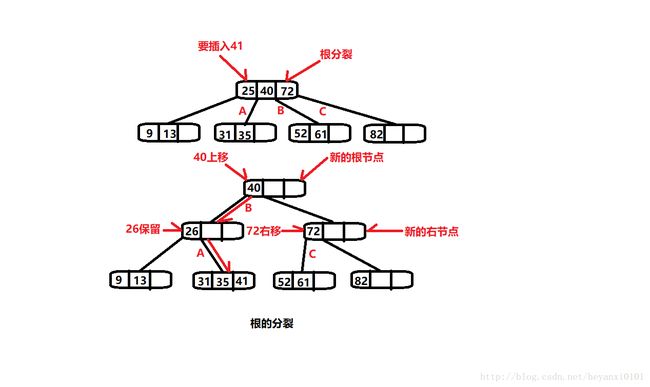
根的分裂：

如果一开始查找插入点时就碰到满的根时，插入过程更加复杂一点：
       · 创建新的根，它是要分裂节点的父节点
       · 创建第二个新节点，它是要分裂节点的兄弟节点
       · 数据项C移到新的兄弟节点中
       · 数据项B移到新的根节点中
       · 数据项A保留在原来的位置上
       · 要分裂节点的最右边的两个子节点断开连接，连到新的兄弟节点中

代码分析

       数据项类

class DataItem {
    public long dData;
    public DataItem(long dd) { dData = dd; }
    public void displayItem() {System.out.println("/" + dData);}
}

       节点类

class Node {
    private static final int ORDER = 4;
    private int numItems;   // 数据项个数
    private Node parent;    // 父节点
    private Node childArray[] = new Node[ORDER];    // 子节点
    private DataItem itemArray[] = new DataItem[ORDER-1];   // 节点数据项

    public Node getChild(int childNum) {return childArray[childNum];}   // 获取当前节点的子节点，通过传入的索引值获取对应的子节点

    public Node getParent() {return parent;}    // 获取父节点

    public boolean isLeaf() {return (childArray[0] == null) ? true : false;}    // 判断是否为叶节点

    public int getNumItems() {return numItems;} // 获取数据项个数

    public DataItem getItem(int index) {return itemArray[index];}   // 获取当前节点的数据项，通过传入的索引值获取对应的数据项

    public boolean isFull() {return (numItems == ORDER-1) ? true : false;}  // 判断该节点的数据项是否已满

    // 连接子节点  输入要插入的子节点的位置  还有子节点
    public void connectChild(int childNum, Node child) {
        childArray[childNum] = child;           // 将要插入的子节点放入当前节点的子节点数组的对应的索引的位置上
        if (child != null) child.parent = this; // 如果插入的节点不为空的话  还要设置新插入节点的父节点为当前节点
    }

    // 拆分子节点  输入要拆分的子节点的位置
    public Node disconnectChild(int childNum) {
        Node tempNode = childArray[childNum];   // 先将要拆分的子节点做一个备份
        childArray[childNum] = null;            // 然后将当前节点的指定子节点的位置 置空
        return tempNode;                        // 返回备份的节点
    }

    // 从当前节点中找一个数据项的位置  输入要查找的值
    public int findItem(long key) {
        for (int j = 0; j < ORDER - 1; j++) {   // 遍历当前节点的所有数据项 
            if (itemArray[j] == null)           // 如果当前的位置没有数据了，那么以后的位置也是没有的
                break;                          // 退出当前的循环
            else if (itemArray[j].dData == key) // 如果找到了对应的值
                return j;                       // 返回对应大的索引
        }
        return -1;                              // 找不到 ，返回-1
    }

    // 从当前节点插入一个数据项 输入要插入的新的数据项
    // 调用该方法的一个前提：当前节点的数据项只有两个或者更少是可以继续插入数据项的（在插入之前会进行一定的检查和判断）
    public int insertItem(DataItem newItem) {
        numItems ++;    // 首先是数据项的个数加1
        long newKey = newItem.dData;    // 获取到数据项的值
        for (int j = ORDER-2; j>=0; j--) {  // 遍历 
            if (itemArray[j] == null)       // 如果当前位置的数据项为空的话 
                continue;                   // 继续查找
            else {                          // 不为空的话
                long itsKey = itemArray[j].dData;   // 首先获取当前位置的数据项的值
                if (newKey < itsKey)                // 如果新的数据项的值小于当前的数据项
                    itemArray[j+1] = itemArray[j];  // 将当前的数据项放在当前位置的后一个位置上
                else {                              // 否则 要插入的数据项大于当前的数据项
                    itemArray[j+1] = newItem;       // 将新插入的数据项放在当前位置的后一个位置上
                    return j+1;                     // 返回插入数据项的索引
                }
            }
        }
        // 如果当前节点的数据项为空 或者插入的数据项是和之前已经存在的数据相比是最小的话
        itemArray[0] = newItem;// 将当前的数据项插入首位
        return 0;   // 返回插入的索引值
    }

    // 删除数据项 返回被删除的数据项 没有指定要删除的位置  所以删除最后一个
    public DataItem removeItem() {
        DataItem temp = itemArray[numItems - 1];    // 先将当前的数据项中的最后一个做一个备份
        itemArray[numItems - 1] = null; // 然后当前节点该处的数据项置为空
        numItems --;    // 数据个数减1
        return temp;    // 返回备份
    }

    // 打印当前节点
    public void displayNode() {
        for (int j=0; j// 遍历并打印所有的数据项
            itemArray[j].displayItem();
        System.out.println("/");
    }
}

       234树

 public class tree234 {
    private Node root = new Node(); // 首先创建一个根

    // 查找数据项
    public int find(long key) {
        Node curNode = root;    // 当前访问的节点
        int childNumber;
        while (true) {
            if ((childNumber = curNode.findItem(key)) != -1) // 如果在当前节点中查找对应的数据项返回不为-1，说明找到了对应的数据项
                return childNumber;     // 直接返回查找数据项对应的索引值
            else if (curNode.isLeaf())  // 如果当前节点为叶子节点 则返回-1 说明树中没有改数据项
                return -1;
            else    // 默认情况下 获取下一个节点
                curNode = getNextChild(curNode, key);
        }
    }

    // 插入一个数据项
    public void insert(long dvalue) {
        Node curNode = root;    // 找插入位置的时候表示当前的节点的局部变量
        DataItem  tempItem = new DataItem(dvalue);  // 创建一个新的数据项对象
        while (true) {
            if (curNode.isFull()) { // 如果当前的节点满了的话 
                split(curNode); // 拆分节点
                curNode = curNode.getParent(); // 差分结束之后 之前的节点变为了子节点 所以先获取其父节点 然后重新开始查询
                curNode = getNextChild(curNode, dvalue);    // 直接查找下一个节点
            } else if (curNode.isLeaf())    // 如果当前节点是一个叶子节点，而且未满
                break;  // 找到了要插入数据的节点 跳出循环 直接进行插入操作
            else
                curNode = getNextChild(curNode, dvalue);    // 没有找到的话 获取下一个子节点节点
        }
        curNode.insertItem(tempItem); // 让当前的节点插入新的数据
    }

    // 拆分一个节点 传入一个需要拆分的节点
    public void split(Node thisNode) {
        DataItem itemB, itemC;
        Node parent, child2, child3;
        int itemIndex;

        itemC = thisNode.removeItem();  // 当前节点中最大的数据项（removeItem方法 默认是删除节点中最大的数据项） 并且已经清空了当前节点的该数据项
        itemB = thisNode.removeItem();  // 当前节点中中间的数据项 并且已经清空了当前节点的该数据项
        child2 = thisNode.disconnectChild(2);   // 当前节点的2号子节点 已经断开了当前节点与2号子节点的连接
        child3 = thisNode.disconnectChild(3);   // 当前节点的3号子节点 已经断开了当前节点与3号子节点的连接
        Node newRight = new Node(); // 新建一个右边的子节点

        if (thisNode == root) { // 如果要拆分的节点为根的话
            root = new Node();  // 创建一个新的根
            parent = root;      // 父节点等于新的根
            root.connectChild(0, thisNode); // 然后让新的根节点与之前的节点相连 连在最左边的位置上
        } else  // 不是根的话
            parent = thisNode.getParent();  // 先获取要拆分节点的父节点

        itemIndex = parent.insertItem(itemB);   // 将要拆分节点的中间的数据插入到父节点中  并且获取到插入的索引
        int n = parent.getNumItems();   // 获取父节点中数据项的个数

        for (int j=n-1; j>itemIndex; j--) { // 
            Node temp = parent.disconnectChild(j);  // 父节点和要拆分的接待你断开连接
            parent.connectChild(j+1, temp); // 父节点和要拆分的原节点重新连接 位置为原要拆分节点的中间的数据项在父节点中位置的左边
        }

        parent.connectChild(itemIndex+1, newRight); // 然后在原要拆分节点新的位置的右边插入新的右边节点

        newRight.insertItem(itemC); // 原节点中最大的数据项 插入新的右节点中
        newRight.connectChild(0, child2); // 新的右节点和原要拆分节点的右边的两个子节点相连 分别放在新节点的 0 1 位置上
        newRight.connectChild(1, child3);
    }

    // 获取下一个子节点 传入一个当前的节点还有一个要查找的数据项的值
    public Node getNextChild(Node theNode, long theValue) {
        int j;
        int numItems = theNode.getNumItems();   // 获取当前节点的数据项的个数
        for (j=0; j// 遍历
            if (theValue < theNode.getItem(j).dData)    // 如果要查找的值小于当前数据项的值
                return theNode.getChild(j); // 返回当前数据项左边的子节点
        }
        // 如果找不到 则返回最后一个子节点
        return theNode.getChild(j);
    }

    // 打印一整棵树
    public void displayTree() {
        recDisplayTree(root, 0, 0);
    }

    // 打印树  传入要从那个节开始打 从那层开始的 哪个节点开始的 前序遍历
    private void recDisplayTree(Node thisNode, int level, int childNumber) {
        System.out.print("level=" + level + " child=" + childNumber + " "); // 先打印当前节点的状况
        thisNode.displayNode();

        int numItems = thisNode.getNumItems();  
        for (int j=0; j1; j++) { // 遍历每一个子节点并打印  递归
            Node nextNode = thisNode.getChild(j);
            if (nextNode != null)   // 如果
                recDisplayTree(nextNode, level+1, j); // 向下层递归
            else
                return; // 递归结束
        }
    }

234树的效率

       2-3-4树中增加每一个节点的数据项数量可以抵偿树的高度的减少。2-3-4树中的查找时间与平衡二叉树如红黑树大概相等，都是O(logN).。