炉石传说 疯狂爆破者空场炸死2个精灵龙的概率

背景介绍

炉石传说中，有一张卡牌叫疯狂爆破者，功能为造成6点伤害，随机分配给其他角色（包括英雄和随从）。

这经常能造成一些意想不到的效果，比如对方空场有2个精灵龙，如果能直接炸死，则能造成巨大的优势，所以本文将要分析一下空场炸死对方2个精灵龙的概率。

分析

1. 使用程序进行模拟

#include "stdio.h"
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;


int main()
{
    int life1=2, life2=2;
    int LOOP = 6;
    int ROUND = 100000000;
    int dies = 0;

    for(int i=0; iint randtarget;
        life1 = life2 = 2;
        for(int j=0; jif(life1>0 && life2>0)
            {
                randtarget = rand()%4;
                if(randtarget==0)
                    --life1;
                else if(randtarget==1)
                    --life2;
            }
            else if(life1==0 && life2>0)
            {
                randtarget = rand()%3;
                if(randtarget==0)
                    --life2;
            }
            else if(life1>0 && life2==0)
            {
                randtarget = rand()%3;
                if(randtarget==0)
                    --life1;
            }
        }
        if(life1==0 && life2==0)
        {
            ++dies;
        }
    }

    printf("%lf\n", dies*1.0/ROUND);

    return 0;
}

模拟10^8次后得到的结果，大约是0.221509

---

2. 使用状态转换分析的方式

如果把两只精灵龙的生命值使用二元组(x,y)表示，即精灵龙1剩余x血，精灵龙2剩余y血，那么总共有(2,2),(2,1),(2,0),(1,2),(1,1),(1,0),(0,2),(0,1)(0,0)这9种状态，依次给它们编号0-8（假定两个英雄不会死亡，即英雄生命生命值都大于6）。我们的初始状态为(2,2)，那么(0,0)就是两条精灵龙都死亡的状态。
于此同时，可以得到每种状态之间的转换概率，比如从(2,2)转换到(2,1)的概率为1/4，从(2,2)转换到(1,2)的概率为1/4，从(2,2)转换到(2,2)的概率为1/2。

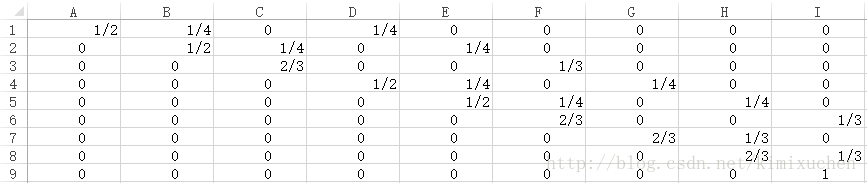
通过分析每种状态，可以得到如下的9X9概率转换矩阵P：

1行A列表示(2,2)->(2,2)的概率，1行I列表示(2,2)->(0,0)的概率，如果只进行一次转换的话(就是只扔一次炸弹)，这个概率显然是0.

疯狂爆破者会扔6次炸弹，那么我们只要计算出P^6即可。这样得到的9X9矩阵就是扔6次炸弹后的状态转换矩阵，得到结果如下：

1行I列的值就是我们要求的(2,2)->(0,0)的概率，为0.2210648，大概为1/5。

其实“马尔科夫链”对此有更专业详细的介绍，上面的过程只是马尔科夫链的一个简单应用。

---

3. 结果对比

仔细观察，会发现模拟方法得到的结果为0.221509，数学分析方法得到的结果为0.2210648，在小数点第四位是有误差的，实验通过提高模拟次数依然无法缩小误差。其实误差的主要原因在于rand()函数。rand()函数随机产生一个0-32767之间的整数，rand()%4可以使得到的0,1,2,3结果出现概率相等，但rand()%3却不能，因为rand()%3等于0和1的情况有10923种，等于2的情况只有10922种，因此在多次模拟后个细微的差别会在小数点之后几位体现出来。这也是为什么模拟法的结果会比数学法的结果有微小的偏高的原因。

结论

炉石传说中疯狂爆破者空场炸死2个精灵龙的概率为0.2210648，解决了很多玩家心中长期存在的一个疑问。
在求解这个问题过程中的分析方法更加重要，马尔科夫链是个强大的工具，值得投入时间学习。