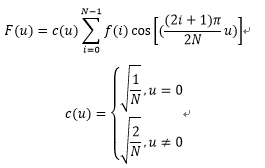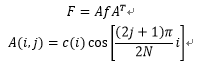DCT算法的原理和优化

未经博主允许，禁止转载!

离散余弦变换（DCT for Discrete Cosine Transform）是与傅里叶变换相关的一种变换，它与离散傅里叶变换类似，但是只使用实数。

这种变化经常被信号处理和图像处理使用，用于对信号和图像（包括静止图像和运动图像）进行有损压缩。在压缩算法中，现将输入图像划分为8*8或16*16的图像块，对每个图像块作DCT变换；然后舍弃高频的系数，并对余下的系数进行量化以进一步减少数据量；最后使用无失真编码来完成压缩任务。解压缩时首先对每个图像块作DCT反变换，然后将图像拼接成一副完整的图像。

大多数自然信号（包括声音和图像）的能量都集中在余弦变换后的低频部分。由于人眼对于细节信息不是很敏感，因此信息含量更少的高频部分可以直接去掉，从而在后续的压缩操作中获得较高的压缩比。

• 1. 一维DCT变换
• 2. 二维DCT变换
• 3. DCT反变换
• 4. 怎样提高二维DCT变换的速度

---

1. 一维DCT变换

一维DCT变换共有8种，最实用的一种公式如下：

其中N是一维数据的元素总数，c(u)系数使得DCT变换矩阵成为正交矩阵，正交特性在二维DCT变换中更能体现其优势。一维DCT变换的复杂度是O(n^2)。

2. 二维DCT变换

二维DCT变换公式如下：

我们将公式变换一下：

可以发现，二维DCT变换其实是在一维DCT变换的基础上，再做一次一维DCT变换。二维DCT也可以写成矩阵相乘的形式：

矩阵A和f必须为长宽均为N的方阵，f不是方阵的情况可以补零再对其做DCT变换。生成矩阵A的matlab代码如下：

A=zeros(N);
 for i=0:N
    for j=0:N
        if i==0
            a=sqrt(1/N);
        else
            a=sqrt(2/N);
        end            
        A(i+1,j+1)=a*cos(pi*(2*j+1)*i/(2*N));
    end
end

二维DCT变换的复杂度达到O(n^4)，所以进行DCT变换的矩阵不宜过大。在实际处理图片的过程中，需要先把矩阵分块，一般分为8*8或16*16大小，这样DCT变换不至于耗费过多的时间。

3. DCT反变换

DCT变换是无损并可逆的，反变换的公式如下：

同样，DCT反变换也可以写成矩阵相乘的形式：

DCT反变换的时间复杂度与DCT变换相同。

4. 怎样提高DCT变换的速度

由于DCT变换的高效，这种变换方法已经广泛应用于信号处理和图像处理，成为许多图像编码国际标准的核心。但随着信息时代的来临和信息量的飞速增长，人们对图像处理的速度要求越来越高，虽然离散余弦变换已经比较高效了，但是能否在DCT变换的基础上，继续提升其速度呢？

我们考虑用并行计算的方法提升速度。并行计算指的是同时使用多种计算资源解决计算问题的一种高效的计算手段。图形处理器（Graphics Processing Unit，缩写GPU）非常擅长大规模并发计算，所以我考虑在GPU上实现并行的二维DCT变换，看能否有效提升二维DCT变换的速度。

我们观察二维DCT变换的公式，不难发现每一个DCT系数的计算，不依赖于任何一个DCT系数，也就是说，任意多个DCT系数的计算，都可以独立进行。所以我考虑对整个矩阵分线程块计算，线程块内再以每一个系数为单位分为线程，每一个DCT系数由一个线程来完成。记矩阵的大小为length*length，块大小为block_len* block_len。

DCT算法的CUDA代码如下，环境为ubuntu 14.04，CUDA版本8.0：

int tidy = blockIdx.x * blockDim.x + threadIdx.x;
    int tidx = blockIdx.y * blockDim.y + threadIdx.y;
    int index = tidx * length + tidy;
    int i;
    float tmp;
    float beta, alfa;
    if (tidx == 0)
        beta = sqrt(1.0 / length);
    else
        beta = sqrt(2.0 / length);
    if (tidy == 0)
        alfa = sqrt(1.0 / length);
    else
        alfa = sqrt(2.0 / length);
    if (tidx < length && tidy < length) {
        for (i = 0; i < length * length; i++) {
            int x = i / length;
            int y = i % length;
            tmp += ((double) f[i])
                    * cos((2 * x + 1) * tidx * PI / (2.0 * length))
                    * cos((2 * y + 1) * tidy * PI / (2.0 * length));
        }
        F[index] = (double) alfa * beta * tmp;
    }
    __syncthreads();
}

由于GPU的控制单元可以把多个访问合并成少的访问，同时，计算每个系数需要访问的数据都完全相同，导致同一个块内的线程对于原矩阵的访问可以达到非常高的效率，所以我直接将块数设置为1，让所有计算系数的线程处于一个块内。

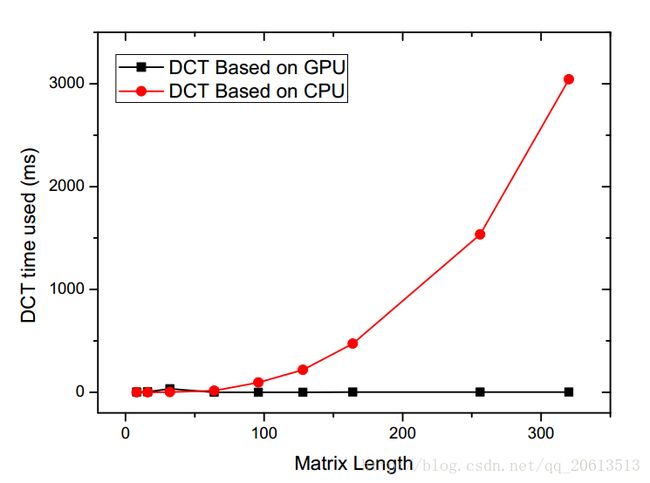
通过实验发现，基于CPU实现的DCT算法随着矩阵的增大，处理时间急剧的上升，而基于GPU实现的并行二维DCT变换算法，耗时非常短，计算速度惊人。

Matrix Length	DCT Based on GPU(ms)	DCT Based on CPU(ms)	speedup
8	2.111	0.111	0.053
16	5.503	0.336	0.061
32	35.1296	2.844	0.081
64	1.105	16.338	14.785
128	2.312	218.512	94.291
256	2.151	1534.86	213.556
320	1.961	3034.05	1547.195

从上表中我们发现，当矩阵比较小的时候，GPU并行计算没有带来优势，反而让DCT变换时间更长了。通过CUDA提供的程序性能分析工具，观察到GPU并行程序的大部分时间不是花在了计算上面，而是CUDA任务的创建上。当矩阵增大之后，CUDA程序的运行时间不再主要取决于Event的创建。而基于CPU的DCT变换的时间基本来自于计算，所以随着矩阵的增大，时间基本呈指数增长。

通过以上内容，我完整的了解了一维和二维DCT变换的详细过程，并且通过GPU并行计算为二维DCT变换加速，实验结果显示，对于比较大的矩阵，基于GPU的二维DCT变换速度得到了巨大的提升，但是在矩阵比较小的应用场景下，CPU更有优势。