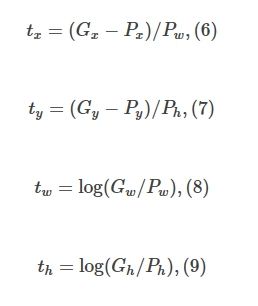目标检测--IOU，bounding box

1.IOU的意义

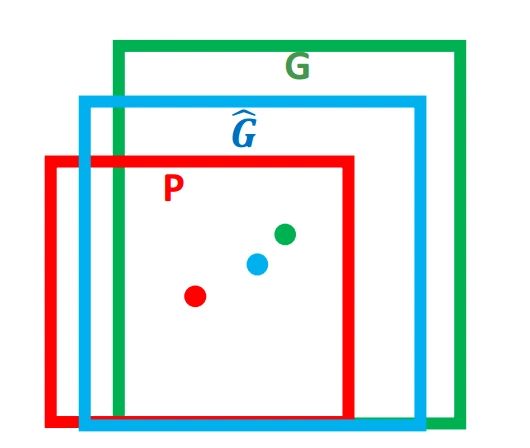
如图红色框和绿色框所示，红色框是Selective Search提取的的Region Proposal记为R，而绿色是我们的实际要达到的检测框（Ground Truth）记为G。那么即便红色的框被分类器识别为飞机，但是由于红色的框定位不准(IoU<0.5)， 那么这张图相当于没有正确的检测出飞机。 如果我们能对红色的框进行微调， 使得经过微调后的窗口跟Ground Truth 更接近， 这样岂不是定位会更准确。 确实，Bounding-box regression 就是用来微调这个窗口的。

IOU就是**(R∩G)/(R∪G)** 。定义这个的目的就是为了在训练时为已标定的Bounding-Box寻找一个能够扩张为该Bounding-Box的Region Proposal，当IOU小于某个值得时候就必须被丢弃，这样的具体原因是因为能够进行Bounding-Box regression的两个框的是差异比较小的，这样才能进行线性模拟（下面会讲述的）。

2 边框回归是什么？

对于窗口一般使用四维向量$(x,y,w,h)$来表示， 分别表示窗口的中心点坐标和宽高。 对于下图, 红色的框 $P$ 代表原始的Region Proposal, 绿色的框 $G$ 代表目标的 Ground Truth， 我们的目标是寻找一种关系使得输入原始的窗口 $P$ 经过映射得到一个跟真实窗口 $G$ 更接近的回归窗口$\hat{G}$。

边框回归的目的既是：给定$(P_x,P_y,P_w,P_h)$寻找一种映射$f$， 使得$f(P_x,P_y,P_w,P_h)=({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h)$并且$({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h)\approx (Gx,Gy,Gw,Gh)$

2.1 边框回归怎么做的？

那么经过何种变换才能从图 2 中的窗口 $P$ 变为窗口$\hat{G}$呢？，用$P$的参数进行计算， 比较简单的思路就是: 平移+尺度放缩

• 先做平移$(\Delta x,\Delta y)$， $\Delta x=P_w{d}_x(P)$,$\Delta y=P_h{d}_y(P)$ 这是R-CNN论文的：
  ${\hat{G}}_x=P_w{d}_x(P)+P_x,(1)$
  ${\hat{G}}_y=P_h{d}_y(P)+P_y,(2)$

• 然后再做尺度缩放$(S_w,S_h)$，$S_w=exp(d_w(P))$，$S_h=exp(d_h(P))$ , 对应论文中：
  ${\hat{G}}_w=P_{w}exp(d_w(P)),(3)$
  ${\hat{G}}_h=P_{h}exp(d_h(P)),(4)$

观察(1)-(4)我们发现， 边框回归学习就是$d_x(P)$，$d_y(P)$，$d_w(P)$，$d_h(P)$这四个变换。下一步就是设计算法那得到这四个映射。

线性回归就是给定输入的特征向量 $X$, 学习一组参数 $W$, 使得经过线性回归后的值跟真实值 Y(Ground Truth)非常接近. 即$Y\approx WX$ 。 那么 Bounding-box 中我们的输入以及输出分别是什么呢？

2.1.1 Input:

$RegionProposal\to P=(Px,Py,Pw,Ph)$，这个是什么？ 输入就是这四个数值吗？其实真正的输入是这个窗口对应的 CNN 特征，也就是 R-CNN 中的 Pool5 feature（特征向量）。 (注：训练阶段输入还包括 Ground Truth， 也就是下边提到的$t_{\ast }=(t_x,t_y,t_w,t_h)$

2.1.2 Output:

需要进行的平移变换和尺度缩放$dx(P),dy(P),dw(P),dh(P)$， 或者说是$\Delta x,\Delta y,S_w,S_h$ 。 我们的最终输出不应该是 Ground Truth 吗？ 是的， 但是有了这四个变换我们就可以直接得到 Ground Truth， 这里还有个问题， 根据(1)~(4)我们可以知道， P 经过 $dx(P),dy(P),dw(P),dh(P)$得到的并不是真实值 $G$， 而是预测值$\hat{G}$。 的确， 这四个值应该是经过 Ground Truth 和 Proposal 计算得到的真正需要的平移量$(t_x,t_y)$和尺度缩放$t_w,t_h$。这也就是 R-CNN 中的(6)~(9)：
$t_x=(G_x-P_x)/P_w,(6)$
$t_y=(G_y-P_y)/P_h,(7)$
$t_w=log(G_w/P_w),(8)$
$t_h=log(G_h/P_h),(9)$

那么目标函数可以表示为 $d_{\ast }(P)=w_{\ast }^T{\Phi }_5(P)$， ${\Phi }_5(P)$是输入 region Proposal 的特征向量，$w_{\ast }$是要学习的参数（$\ast$表示 $x,y,w,h$， 也就是每一个变换对应一个目标函数） , $d_{\ast }(P)$是得到的预测值。 我们要让预测值跟真实值$t_{\ast }=(t_x,t_y,t_w,t_h)$差距最小， 得到损失函数为：
$Loss={\sum }_i^N(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5(P^i){)}^2$

函数优化目标为：
$W_{\ast }=argmi{n}_{w_{\ast }}{\sum }_i^N(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5(P^i){)}^2+\lambda ||{\hat{w}}_{\ast }|{|}^2)$

2.2 为什么宽高尺度会设计这种形式？

这边我重点解释一下为什么设计的$tx,ty$为什么除以宽高，为什么$t_w,t_h$会有log形式！！！

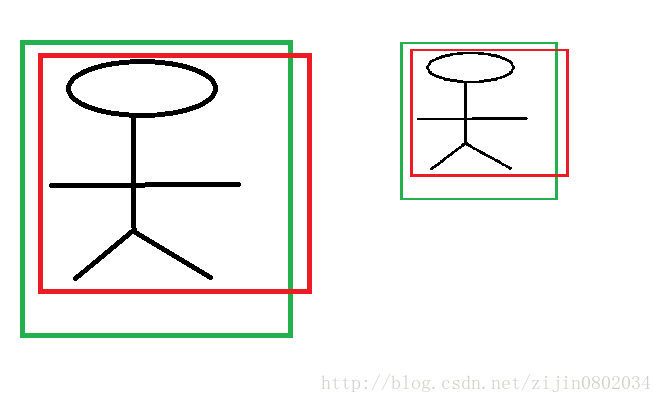
首先CNN具有尺度不变性， 以图3为例：

2.2.1 x,y 坐标除以宽高

上图的两个人具有不同的尺度，因为他都是人，我们得到的特征相同。假设我们得到的特征为${\varphi }_1,{\varphi }_2$，那么一个完好的特征应该具备${\varphi }_1={\varphi }_2$。ok，如果我们直接学习坐标差值，以$x$坐标为例，$x_i,p_i$分别代表第$i$个框的$x$坐标，学习到的映射为$f$, $f({\varphi }_1)=x_1-p_1$，同理$f({\varphi }_2)=x_2-p_2$。从上图显而易见，$x_1-p_1\ne x_2-p_1$。也就是说同一个$x$对应多个$y$，这明显不满足函数的定义。边框回归学习的是回归函数，然而你的目标却不满足函数定义，当然学习不到什么。

2.2.2 宽高坐标Log形式

我们想要得到一个放缩的尺度，也就是说这里限制尺度必须大于0。我们学习的$t_w,t_h$怎么保证满足大于0呢？直观的想法就是EXP函数，如公式(3), (4)所示，那么反过来推导就是Log函数的来源了。

2.2.3 为什么IoU较大，认为是线性变换？

当输入的 Proposal 与 Ground Truth 相差较小时(RCNN 设置的是 IoU>0.6)， 可以认为这种变换是一种线性变换， 那么我们就可以用线性回归来建模对窗口进行微调， 否则会导致训练的回归模型不 work（当 Proposal跟 GT 离得较远，就是复杂的非线性问题了，此时用线性回归建模显然不合理）。这里我来解释：

Log函数明显不满足线性函数，但是为什么当Proposal 和Ground Truth相差较小的时候，就可以认为是一种线性变换呢？大家还记得这个公式不？参看高数1。
$li{m}_{x=0}log(1+x)=x$

现在回过来看公式(8):

$t_w=log(G_w/P_w)=log(\frac{G_w+P_w-P_w}{P_w})=log(1+\frac{G_w-P_w}{P_w})$

当且仅当$G_w-P_w=0$的时候，才会是线性函数，也就是宽度和高度必须近似相等。

other

如上图中P是训练时生成的边框（要满足IOU的条件）$\hat{G}$为中间的经过回归的边框，G是我们训练样本中标定的边框。我们该如何从P生成到$\hat{G}$呢？首先我们需要知道该如何确定一个边框在一幅图的位置对于窗口一般使用四维向量(x,y,w,h)来表示， 分别表示窗口的中心点坐标和宽高。我们要将P变换到$\hat{G}$只需要进行平移后缩放就可以了，这是几何上的直观想法（本文中$\hat{G}$与P变换后的窗体指代一个对象）

边框回归学习就是$d_x(P)$，$d_y(P)$，$d_w(P)$，$d_h(P)$这四个变换。下一步就是设计算法那得到这四个映射。
那么问题就来了，我们从图形中获得的数据不可能真的是坐标，不然就成了在某个位置固定了对应得一个变换方法而不管该位置的图形到底是什么东西。我们获得的对象是该Region Proposal的特征向量，这也是十分合理的，想象一下人在确定一幅图中某个固定大小区域的对象时，如该区域只有对象的一部分图片，我们也是进行扩大视野最后就能看到整个对象了呀，最后的视野也就是Ground Truth。而人接受的输入是像素点，那么对应的在回归中就接受特征向量。
在人接受到图片是就知道该如何移动自己的目光来寻找整个对象，相当于人知道当前看到的部分在实际物体对象中所处的位置后，就知道该如何变换自己的目光和视野范围，如看到左半脸就知道将目光平移到右边再扩大自己的视野。类似的在接收到特定Region Proposal的特征向量，算法应该知道朝什么方向移动和如何进行尺度缩放（这些都是从训练中习得的）。这使用数学语言就是一种由特征向量向$d_x(P)$，$d_y(P)$，$d_w(P)$，$d_h(P)$的映射关系！
如何能得到该关系呢，还是要进行训练，下图是我们追求的尺度变换的方法，也就是监督学习中的类似于label的量。

那么我们实际做的尺度变换可以定义为$d_{\ast }=(P)=w_{\ast }^T{\Phi }_5(P)$，${\Phi }_5(P)$是输入 Proposal 的特征向量，$w_{\ast }$是要学习的参数（$\ast$表示 $x,y,w,h$， 也就是每一个变换对应一个目标函数，也就是刚刚说的映射关系）,$d_{\ast }(P)$是得到的预测值。 我们要让预测值跟真实值$t_{\ast }=(t_x,t_y,t_w,t_h)$差距最小， 得到损失函数为：

$Loss={\sum }_i^N(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5(P^i){)}^2$

优化函数为：

$W_{\ast }=argmi{n}_{w_{\ast }}{\sum }_i^N(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5(P^i){)}^2+\lambda ||{\hat{w}}_{\ast }|{|}^2)$

reference：
https://segmentfault.com/a/1190000011918305
https://blog.csdn.net/zijin0802034/article/details/77685438