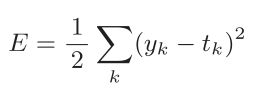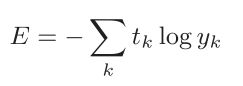深度学习理论基础13-损失函数

开始之前先认识机器学习的几个概念性的东西：

深 度 学 习 有 时 也 称 为 端 到 端 机 器 学 习（end-to-end machinelearning）。

机器学习中，一般将数据分为训练数据和测试数据(或监督数据)两部分来进行学习和实验等。

只对某个数据集过度拟合的状态称为过拟合（over fitting）。

避免过拟合也是机器学习的一个重要课题。

神经网络的学习通过某个指标表示现在的状态，以这个指标为基准，寻找最优权重参数。

神经网络的学习中所用的指标称为损失函数（loss function）。

这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

损失函数是表示神经网络性能的“恶劣程度”。

无聊的定义看完了，立即进入今天的主题吧。

--------损失函数之均方误差--------

y k 是表示神经网络的输出，t k 表示监督数据，k表示数据的维数

用Python语言这么表示：

#均方差
def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

下面用一个实例来说明均方误差的使用方法：

def main():
    # 正确的结果为2
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
    #第一个模型认为结果为2的概率为0.6
    y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    error_1=mean_squared_error(np.array(y1), np.array(t))
    # 第一个模型认为结果为2的概率为0.1
    y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    error_2=mean_squared_error(np.array(y2), np.array(t))
    print(error_1) #输出0.09750000000000003
    print(error_2) #输出0.5975


if __name__=='__main__':
    main()

可以看到，模拟的第一个模型预测有0.6的概率为2.第二个模型认为结果为2的概率为0.1.

均方误差也给出了符合我们认知的结果。在糟糕程度方面的得分，模型二完胜。

--------交叉熵误差--------

log表示以e为底数的自然对数

y k 是神经网络的输出

t k 是正确解标签

又因为除了正确标签以外的位置都为0.所以其实本式的计算有点奇怪：

t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] #对应t k----正确解标签

y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]  #对应y k----神经网络的输出

把正确解标签带入的时候，我们发现，所有1以外的值都为0.

所以本式等同−log t2，也就是−log0.6 = 0.51

用Python代码实现：

#交叉熵误差
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

接下来讨论为什么平白无故多了一个极小值delta。下面是y=log x的图像化表示

 

可以发现，当x靠近0时，y急速变小。delta被引入以作为保护措施，防止出现负无穷的情况。

因为计算机对负无穷束手无策。

接下来把上面的main函数中的损失函数由均方误差改为交叉熵误差。

def main():
    # 正确的结果为2
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
    #第一个模型认为结果为2的概率为0.6
    y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    # error_1=mean_squared_error(np.array(y1), np.array(t))
    error_1 = cross_entropy_error(np.array(y1), np.array(t))
    # 第一个模型认为结果为2的概率为0.1
    y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    # error_2=mean_squared_error(np.array(y2), np.array(t))
    error_2 = cross_entropy_error(np.array(y2), np.array(t))
    # print(error_1) #输出0.09750000000000003
    # print(error_2) #输出0.5975
    print(error_1) #输出0.510825457099338
    print(error_2) #输出2.302584092994546

if __name__=='__main__':
    main()

再一次得到让人满意的结果。

现在我们可以评估一个模型的糟糕程度了。

但是，有句话这么说的，判断一个鸡蛋是不是臭的，大可不必全部吃完才下结论。

对于模型评估，我们也可以进行抽样评估。例如几千万份数据里里仅抽取几百份进行评估。

然后对样本进行mini-batch学习，即小批量的计算损失函数。然后取平均值，以近似的得到模型的可靠指数。

用数学公式表示为：

蓝色的部分求出每一个的槽糕程度，红色部分代表把选取的数据集的槽糕程度相加后得到平均糟糕程度。

按照惯例，先把需要做的事情列出来：

1.获得数据集

2.随机抽取一定数量的数据集

3.用损失函数计算抽取的数据集的性能

第一步，获得数据集

from yuan.dataset.mnist import load_mnist


# 1.第一步，获得数据集
def get_data():
    #通过这个函数，获得训练集和测试集
    (x_train, t_train), (x_test, t_test) = \
        load_mnist(normalize=True, flatten=True, one_hot_label=False)
    # 后面只用到测试集，所以只返回这俩(因为模型是训练好的，所以用不到训练集)
    return x_test, t_test

这个代码前面用过。

第二步.随机抽取一定数量的数据集

#抽取一定数量数据集
def get_random_set(x_train,t_train):
    train_size = x_train.shape[0]
    batch_size = 10
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    return x_batch,t_batch

第三步.用损失函数计算抽取的数据集的性能

def cross_entropy_error(y, t):
    #y为模型的输出,如果为1维的，那就转化为2维的。
    #原因在于配合后面的y.shape，以便得到正确的样本数量
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    #正如前面所说，batch_mini就是把样本内的性能平均值
    return -np.sum(t * np.log(y + 1e-7)) / batch_size

到这里为止，我们已经可以把一小批样本求出平均槽糕度了。

这个平均糟糕度近似了反应了这个模型的槽糕程度。

别着急放松，因为真实结果有两种表示方式。譬如结果为2，

我们用独热编码这么表示[0,0,1,0,0,0,0,0,0,0]

而不使用读热编码只是使用一个数字2作为结果。

以上都是基于独热编码为前提进行的计算，如果用非独热编码则是另外一个故事了。

def cross_entropy_error(y, t):
    #y为模型的输出,如果为1维的，那就转化为2维的。
    #原因在于配合后面的y.shape，以便得到正确的样本数量
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    #正如前面所说，batch_mini就是把样本内的性能平均值
    # return -np.sum(t * np.log(y + 1e-7)) / batch_size
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

你已经注意到，只是最后一行代码发生了变化。

如果更加精确一点，就是t * np.log(y + 1e-7)替换为了np.log(y[np.arange(batch_size), t] + 1e-7)

所以只需要证明这俩货其实是一回事就行了。

假如真实结果为2，那么，t * np.log(y + 1e-7)其实就是

0*np.log(y[i][0])+0*np.log(y[i][1])+1*np.log(y[i][2])+...+0*np.log(y[i][n])=np.log(y[i][2])

其中i代表np.array([0,1....n])

而np.log(y[np.arange(batch_size), t] + 1e-7)当中，因为结果用单个2表示的，所以t就是2.

而np.arange(batch_size)同样是np.array([0,1....n])。

所以这俩货表示的其实是一回事。

--------为何要设定损失函数--------

我们的目的是提高图片的正确率，为什么不直接使用图片的正确率作为衡量标准呢？

假设某个神经网络正确识别出了100笔训练数据中的32笔，此时识别精度为32 %。

如果以识别精度为指标，即使稍微改变权重参数的值，识别精度也仍将保持在32 %，

不会出现变化。而如果把损失函数作为指标，则当前损失函数的值可以表示为0.92543 . . . 这样的值。

随参数的微调，会发生变化。机器学习需要依靠斜率不会为0这一条件。只有连续的变化才会满足这一条件。

这也是阶跃函数不能作为机器学习激活函数的原因。

好了，关于损失函数就到这里了。再见！