【网络优化】超轻量级网络SqueezeNet算法详解
Iandola, Forrest N., et al. “SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 1MB model size.” arXiv preprint arXiv:1602.07360 (2016).
本文考察了深度学习中除了精度之外的另一个重要因素:模型大小。有两处值得学习的亮点:
- 给出了一个分类精度接近AlexNet1的网络,模型缩小510倍
- 归纳了缩小模型尺寸时的设计思路
复习:卷积层的参数个数。
输入通道 ci ,核尺寸 k ,输出通道 co ,参数个数为: ci×k2×co 。
以AlexNet第一个卷积层为例,参数量达到:3*11*11*96 = 34848。
作者提供的源码请戳这里,各个主流框架均有实现。
基础模块
在当下许多深度学习的文章中都使用了模块化的设计思想,远者有AlexNet中反复出现的conv+relu+pool模式;近者有用于人体姿态分析的Stacked Hourglass算法(参看这篇博客)
本文使用的基础模块称为fire:

包含三个卷积层(蓝色),步长均为1。分为squeeze和expand两部分,分别压缩和扩展数据(灰色矩形)的通道数。
expand部分中,两个不同核尺寸的结果通过串接层(黄色)合并输出。
fire模块有三个可调参数:
- s1 : squeeze部分,1×1卷积层的通道数
- e1 : expand部分,1×1卷积层的通道数
- e3 : expand部分,3×3卷积层的通道数
输入输出尺寸相同。输入通道数不限,输出通道数为 e1+e3 。
在本文提出的SqueezeNet结构中, e1=e3=4s1 。
网络结构
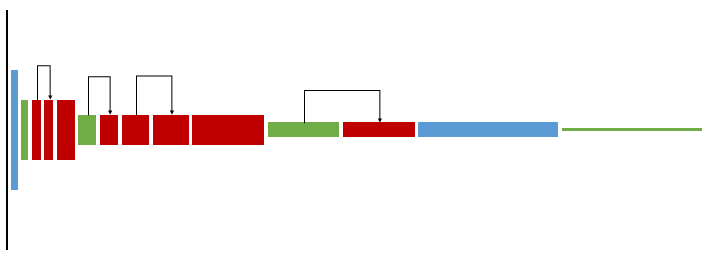
整个网络包含10层。
第1层为卷积层(蓝色),缩小输入图像,提取96维特征。
第2到9层为fire模块(红色),每个模块内部先减少通道数(squeeze)再增加通道数(expamd)。每两个模块之后,通道数会增加。
在1,4,8层之后加入降采样的max pooling(绿色),缩小一半尺寸。
第10层又是卷积层(蓝色),为小图的每个像素预测1000类分类得分。
最后用一个全图average pooling(绿色)得到这张图的1000类得分,使用softmax函数归一化为概率。

这是一个全卷积网络,避免了如今越来越不受待见的全连接层。由于最后一层提供了全图求平均操作,可以接受任意尺寸的输入。当然,输入还是需要归一化到大致相当的尺寸,保持统一尺度。
全连接层的参数多,对性能提升帮助不大,现在往往被pooling代替。
这个网络达到了和AlexNet相当的分类精度,但模型缩小了50倍:
| architecture | model size | top-1 accuracy | top-5 accuracy |
|---|---|---|---|
| AlexNet | 240MB | 57.2% | 80.3% |
| SqueezeNet | 4.8MB | 57.5% | 80.3% |
参数压缩
在网络结构确定的前提下,还可以进一步压缩其中的参数。本文使用了第二作者的Deep Compression2方法,包含裁剪,量化,编码三个手段。
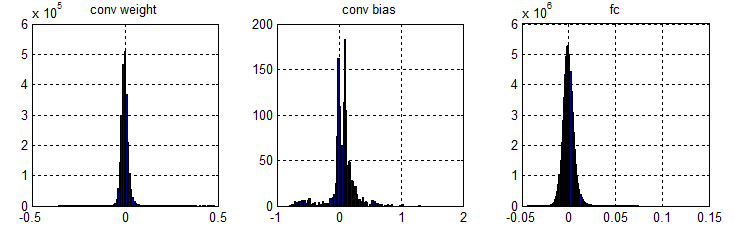
AlexNet中卷积层的weight、bias以及全连层参数分布如下所示。可以看出:全连层参数和卷积层weight占绝大多数,卷积层的bias只占极小部分。
参数压缩针对卷积层的weight和全连层参数。每一层的参数单独压缩。
裁剪
由前图可以看出,绝大部分参数集中在0附近。
裁剪操作的第一步,把网络中所有绝对值小于门限的参数置0;非零参数再次训练进行优化。
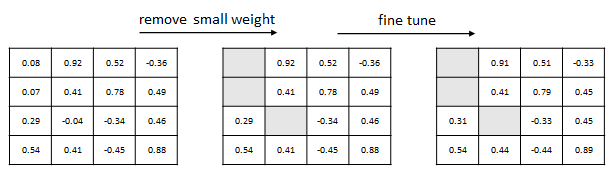
第二步,用下标方法表示剩余的参数:记录非零参数值和其在数组中的下标。
论文声称使用compressed sparse row方法进行压缩,实际源码中并没有。
下标中相邻元素差值不会超过数组长度。为了进一步压缩,把下标表示成差分形式。
例:稀疏矩阵
⎡⎣⎢⎢⎢0500080600300000⎤⎦⎥⎥⎥A = [ 5 8 3 6 ], IA = [4 5 10 13]
差分形式:IA = [4 1 5 3]
差分形式的IA动态范围大大缩小,可以用较少的比特数(4)进行编码。
当差值超出当前比特数能表示的范围后,在中间插入一个值为0的“非零元素”。
量化(Quantization)
首先,用K均值把所有参数聚成 2n 个类。
之后,保持同一聚类内参数相等,对网络进行调优。在梯度下降时,归于同一类的节点的梯度相加,施加到该类的聚类中心上。
最后,使用n比特编码的聚类中心替代原有参数。

Deep Compression论文:卷积层,n=8; fc层,n=4。SqueezeNet中全部为卷积层,n=6。
问题:同类节点的梯度为什么相加?不是应该求平均吗?
编码(Huffman Encoding)
现在需要存储的主要数据有二:编码为n位的非零数据取值;编码为4位的非零元素下标。
这两者的分布都不均匀,可以使用Huffman编码进一步压缩存储。源码中没有实现。
模型存储结构
压缩后的二进制模型按层存储,当前层有nz个非零元素,分为如下4个部分:
| name | type | size | note |
|---|---|---|---|
| codebook | float32 | 2^n | 码书 |
| bias | float32 | 输出通道数 | 无压缩 |
| spm_stream | uint8 | nz−18/n+1 | 非零元素取值,n位编码$ |
| ind_stream | uint8 | nz−18/4+1 | 非零元素下标,4位编码$ |
经过Deep Compression压缩,模型进一步缩小了10倍,仍然保持原有精度。
| architecture | model size | top-1 accuracy | top-5 accuracy |
|---|---|---|---|
| AlexNet | 240MB | 57.2% | 80.3% |
| SqueezeNet | 4.8MB | 57.5% | 80.3% |
| SqueezeNet+DeepCompression | 0.66MB | 57.5% | 80.3% |
设计思路
本文还花费较大篇幅介绍了设计网络时的心得体会,颇具启发性。
参数组合
每层fire模块的三个参数如果单独设计,需要尝试的组合太多。需要使用超参数进行规划:
- 首个fire模块中包含base个3×3核;每隔freq个fire模块,3×3模块增加incre个。
- expand部分中,3×3核占expand中核总数比例为pct。
- squeeze中核数与expand中核数比例为sr。
sr和pct增大可以提升准确率,但模型尺寸增大。本文取sr=0.125,pct=0.5。
大尺度结构
在通道数相同的层之间,添加旁路相加结构可以明显提升准确性(源码未实现)。
带有卷积的旁路结构可以在任意层之间添加,准确性提升较小,模型增大。
压缩:有的放矢
问:如何确定哪些层不重要?
答:逐个将每一层50%参数置零,查看模型性能。对性能影响不大的层,不重要。
问:不重要的怎么办?
答:Deep Compression中使用较少比特数表达。
问:重要的层呢?
答:增加expand部分中的输出通道数,进一步提升准确率。
SDS训练法
本文还有一个神奇的发现:使用裁剪之后的模型为初始值,再次进行训练调优所有参数,正确率能够提升4.3%。
稀疏相当于一种正则化,有机会把解从局部极小中解放出来。这种方法称为DSD(dense->sparse->dense)。
- A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012. ↩
- Iandola, Forrest N., et al. “SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 1MB model size.” arXiv preprint arXiv:1602.07360 (2016). ↩