广度优先搜索(宽度优先搜索,BFS)和深度优先搜索(DFS)算法的应用非常广泛,本篇文章主要介绍BFS与DFS的原理、实现和应用。
深度优先搜索
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。
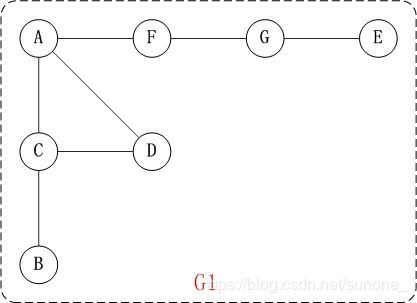
第1步:访问A。
第2步:访问(A的邻接点)C。在第1步访问A之后,接下来应该访问的是A的邻接点,即"C,D,F"中的一个。但在本文的实现中,顶点ABCDEFG是按照顺序存储,C在"D和F"的前面,因此,先访问C。
第3步:访问(C的邻接点)B。在第2步访问C之后,接下来应该访问C的邻接点,即"B和D"中一个(A已经被访问过,就不算在内)。而由于B在D之前,先访问B。
第4步:访问(C的邻接点)D。在第3步访问了C的邻接点B之后,B没有未被访问的邻接点;因此,返回到访问C的另一个邻接点D。
第5步:访问(A的邻接点)F。 前面已经访问了A,并且访问完了"A的邻接点B的所有邻接点(包括递归的邻接点在内)";因此,此时返回到访问A的另一个邻接点F。
第6步:访问(F的邻接点)G。
第7步:访问(G的邻接点)E。
因此访问顺序是:A -> C -> B -> D -> F -> G -> E。
当然,上图是基于无向图,具体的代码在文章后面实现。
广度优先搜索
广度优先搜索算法(Breadth First Search),又称为"宽度优先搜索"或"横向优先搜索",简称BFS。
它的思想是:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2…的顶点。
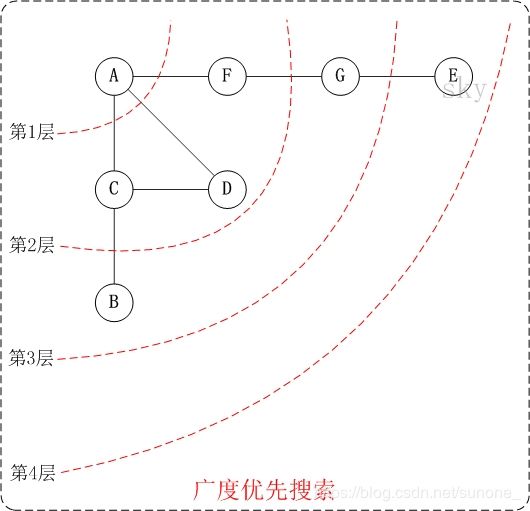
第1步:访问A。
第2步:依次访问C,D,F。在访问了A之后,接下来访问A的邻接点。前面已经说过,在本文实现中,顶点ABCDEFG按照顺序存储的,C在"D和F"的前面,因此,先访问C。再访问完C之后,再依次访问D,F。
第3步:依次访问B,G。在第2步访问完C,D,F之后,再依次访问它们的邻接点。首先访问C的邻接点B,再访问F的邻接点G。
第4步:访问E。在第3步访问完B,G之后,再依次访问它们的邻接点。只有G有邻接点E,因此访问G的邻接点E。
因此访问顺序是:A -> C -> D -> F -> B -> G -> E。
代码实现
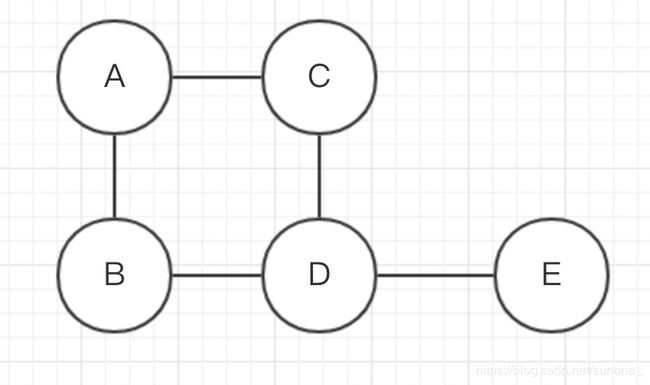
存储顺序为A->B->C->D->E.
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class DFSAndBFS {
//初始化顶点个数,当然也可以自己写一个函数由用户输入自定义图,这里重点不是图的构造
private int numVertexes = 5;
//初始化顶点
private String[] vex;
//邻接矩阵,表明了顶点的关系
private int[][] acr;
private DFSAndBFS()
{
vex= new String[]{"A", "B", "C", "D", "E"};
acr= new int[][]{
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 0},
{0, 1, 0, 0, 1},
{1, 0, 1, 0, 0},
{0, 0, 1, 0, 0}
};
}
private void printGraph(DFSAndBFS g)
{
System.out.println("图中各顶点的关系如下图所示(邻接矩阵,1代表两顶点有边,0代表无)");
System.out.print(" ");
for(int i=0;i<g.numVertexes;i++)
{
System.out.print(g.vex[i]+" ");
}
for(int i=0;i<g.numVertexes;i++)
{
System.out.println();
System.out.print(g.vex[i]+" ");
for(int j=0;j<g.numVertexes;j++)
{
System.out.print(g.acr[i][j]+" ");
}
}
}
//深度优先遍历,递归算法
private void DFSTraverse(DFSAndBFS g)
{
//建立访问数组
boolean []visited=new boolean [g.numVertexes];
//初始化 访问顶点
for(int i=0;i<visited.length;i++)
visited[i]=false;
//对未访问顶点调用DFS
for(int i=0;i<visited.length;i++)
if(!visited[i])
DFS(g,i,visited);
}
//从顶点i开始进行的深度优先搜索DFS
private void DFS(DFSAndBFS g, int i, boolean[] visited) {
visited[i]=true;
System.out.print(g.vex[i]+" ");
for(int j=0;j<g.numVertexes;j++)
{
if(g.acr[i][j]>0 && !visited[j])
DFS(g,j,visited);
}
}
//深度优先遍历,非递归算法
private void DFS(DFSAndBFS g){
boolean[] visited = new boolean[numVertexes];
Stack<Integer> stack =new Stack<Integer>();
for(int i=0;i<g.numVertexes;i++){
if(!visited[i]){
visited[i]=true;
System.out.print(g.vex[i]+" ");
stack.push(i);
}
while(!stack.isEmpty()){
int k = stack.pop();
for(int j=0;j<g.numVertexes;j++){
if(g.acr[k][j]==1&& !visited[j]){
visited[j]=true;
System.out.print(g.vex[j]+" ");
stack.push(j);
break;
}
}
}
}
}
//广度优先搜索
private void BFS(DFSAndBFS g)
{
int i=0;
Queue<Integer> q=new LinkedList<Integer>();
//建立访问数组
boolean visited[]=new boolean[numVertexes];
//初始化 访问顶点
for(i=0;i<g.numVertexes;i++)
visited[i]=false;
//对每个顶点做循环
for( i=0;i<g.numVertexes;i++)
{
if(!visited[i])
{
visited[i]=true;
System.out.print(g.vex[i]+" ");
q.offer(i);
while(!q.isEmpty())
{
i=q.poll();
for(int j=0;j<g.numVertexes;j++)
{
if(g.acr[i][j]>0 && !visited[j])
{
visited[j]=true;
System.out.print(g.vex[j]+" ");
q.offer(j);
}
}
}
}
}
}
public static void main(String []args)
{
DFSAndBFS g=new DFSAndBFS();
g.printGraph(g);
System.out.println();
System.out.println("深度优先搜索(递归)结果:");
g.DFSTraverse(g);
System.out.println();
System.out.println("深度优先搜索(非递归)结果:");
g.DFS(g);
System.out.println();
System.out.println("广度优先搜索结果:");
g.BFS(g);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
测试结果:
图中各顶点的关系如下图所示(邻接矩阵,1代表两顶点有边,0代表无)
A B C D E
A 0 1 0 1 0
B 1 0 1 0 0
C 0 1 0 0 1
D 1 0 1 0 0
E 0 0 1 0 0
深度优先搜索(递归)结果:
A B C E D
深度优先搜索(非递归)结果:
A B C E D
广度优先搜索结果:
A B D C E
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
以上就是本篇文章讲述的DFS与BFS了,还有一些基于树去做DFS和BFS的,当然我们的树也可以转化为图的。推荐一篇关于树的DFS于BFS。如链接:https://www.cnblogs.com/xiaolovewei/p/7763867.html。
如果您有什么疑问、想法或者建议都可以联系我哦。联系方式:[email protected]发送邮件。
转载或者引用内容请注明出处。