互联网公司常见面试算法题库
1、假设淘宝一天有5亿条成交数据,求出销量最高的100个商品并给出算法的时间复杂度。
先用哈希,统计每个商品的成交次数,然后再用在N个数中找出前K大个数的方法找出成交次数最多的前100个商品。
优化方法:可以把5亿个数据分组存放,比如放在5000个文件中。这样就可以分别在每个文件的10^6个数据中,用哈希+堆统计每个区域内前100个频率最高的商品,最后求出所有记录中出现频率最高的前100个商品。
2、有10亿个杂乱无章的数,怎样最快地求出其中前1000大的数。
方法一: 建一个1000个数的最小堆,然后依次添加剩余元素,如果大于堆顶的数(堆中最小的),将这个数替换堆顶,并调整结构使之仍然是一个最小堆,这样,遍历完后,堆中的1000个数就是所需的最大的1000个。算法的时间复杂度为O(nlogk)=n*log1000=10n(n为10亿,k为1000)。
优化的方法:分治法。可以把所有10亿个数据分组存放,比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的10000个数,合并到一起再找出最终的结果。
优化的方法:如果这10亿个数里面有很多重复的数,先通过Hash法,把这10亿个数字去重复,这样如果重复率很高的话,会减少很大的内存用量,从而缩小运算空间,然后通过分治法或最小堆法查找最大的1000个数。
方法二:
1.用每一个BIT标识一个整数的存在与否,这样一个字节可以标识8个整数的存在与否,对于所有32位的整数,需要512Mb,所以开辟一个512Mb的字符数组A,初始全0
2.依次读取每个数n,对于数n,n存放在A[N>>3]中的某个bit,因此,将A[n>>3]设置为A[n>>3]|(1<<(n%8))(这里是1左移几位),相当于将每个数的对应位设置为1
3.在A中,从数组尾开始向前遍历,从大到小读取1000个值为1的数,就是最大的1000个数了。
这样读文件就只需要1遍,在不考虑内存开销的情况下,应该是速度最快的方法了。
2、给一列无序数组,求出中位数并给出算法的时间复杂度。
若数组有奇数个元素,中位数是a[(n-1)/2];若数组有偶数个元素,中位数为a[n/2-1]和a[n/2]两个数的平均值。这里为方便起见,假设数组为奇数个元素。
思路一:把无序数组排好序,取出中间的元素。时间复杂度取决于排序算法,最快是快速排序,O(nlogn),或者是非比较的基数排序,时间为O(n),空间为O(n)。这明显不是我们想要的。
思路二:采用快速排序的分治partition过程。任意挑一个元素,以该元素为支点,将数组分成两部分,左边是小于等于支点的,右边是大于支点的。如果左侧长度正好是(n-1)/2,那么支点恰为中位数。如果左侧长度<(n-1)/2, 那么中位数在右侧,反之,中位数在左侧。 进入相应的一侧继续寻找中位数。
-
//快速排序的分治过程找无序数组的中位数 -
int partition(int a[], int low, int high) //快排的一次排序过程 -
{ -
int q = a[low]; -
while (low < high) -
{ -
while (low < high && a[high] >= q) -
high--; -
a[low] = a[high]; -
while (low < high && a[low] <= q) -
low++; -
a[high] = a[low]; -
} -
a[low] = q; -
return low; -
} -
int findMidium(int a[], int n) -
{ -
int index = n / 2; -
int left = 0; -
int right = n - 1; -
int q = -1; -
while (index != q) -
{ -
q = partition(a, left, right); -
if (q < index) -
left = q + 1; -
else if (q>index) -
right = q - 1; -
} -
return a[index]; -
}
思路三:将数组的前(n+1)/2个元素建立一个最小堆。然后,对于下一个元素,和堆顶的元素比较,如果小于等于,丢弃之,如果大于,则用该元素取代堆顶,再调整堆,接着看下一个元素。重复这个步骤,直到数组为空。当数组都遍历完了,(堆中元素为最大的(n+1)/2个元素,)堆顶的元素即是中位数。
-
//构建最小堆找无序数组的中位数 -
void nswap(int& i, int& j) -
{ -
i = i^j; -
j = i^j; -
i = i^j; -
} -
void minHeapify(int a[], int i, int len) -
{ -
int temp; -
int least = i; -
int l = i * 2 + 1; -
int r = i * 2 + 2; -
if (l < len && a[l] < a[least]) -
least = l; -
if (r < len && a[r] < a[least]) -
least = r; -
if (least != i) -
{ -
nswap(a[i], a[least]); -
minHeapify(a, least, len); -
} -
} -
void buildMinHeap(int a[], int len) -
{ -
for (int i = (len-2) / 2; i >= 0; i--) -
{ -
minHeapify(a, i, len); -
} -
} -
int findMidium2(int a[], int n) -
{ -
buildMinHeap(a, (n + 1) / 2); -
for (int i = (n + 1) / 2; i < n; i++) -
{ -
if (a[i] > a[0]) -
{ -
nswap(a[i], a[0]); -
minHeapify(a, 0,(n + 1) / 2); -
} -
} -
return a[0]; -
}
引申一:
查找N个元素中的第K个小的元素
编程珠玑给出了一个时间复杂度O(N)的解决方案。该方案改编自快速排序。
经过快排的一次划分,
1)如果左半部份的长度>K-1,那么这个元素就肯定在左半部份了
2)如果左半部份的长度==K-1,那么当前划分元素就是结果了。
3)如果。。。。。。。
也可以用来查找N个元素中的前K个小的元素,前K个大的元素。。。。等等。
引申二:
查找N个元素中的第K个小的元素,假设内存受限,仅能容下K/4个元素。
分趟查找,
第一趟,用堆方法查找最小的K/4个小的元素,同时记录剩下的N-K/4个元素到外部文件。
第二趟,用堆方法从第一趟筛选出的N-K/4个元素中查找K/4个小的元素,同时记录剩下的N-K/2个元素到外部文件。
。。。
第四趟,用堆方法从第一趟筛选出的N-K/3个元素中查找K/4个小的元素,这是的第K/4小的元素即使所求。
3、输入一个整型数组,求出子数组和的最大值,并给出算法的时间复杂度。
设b[i]表示a[0...i]的子数组和的最大值,且b[i]一定包含a[i],即:
sum为子问题的最优解,
1. 包含a[i],即求b[i]的最大值,在计算b[i]时,可以考虑以下两种情况,因为a[i]要求一定包含在内,所以
1) 当b[i-1]>0, b[i] = b[i-1]+a[i]
2) 当b[i-1]<=0, b[i] = a[i], 当b[i-1]<=0,这时候以a[i]重新作为b[i]的起点。
2. 不包含a[i],即a[0]~a[i-1]的最大值(即0~i-1局部问题的最优解),设为sum
最后比较b[i]和 sum,即,如果b[i] >sum ,即b[i]为最优解,然后更新sum的值.
在实现时,bMax代表 b[k], sum更新前代表前一步子问题的最优解,更新后代表当前问题的最优解。实现如下:
-
//求数组的子数组和的最大值,时间复杂度为O(n) -
int maxSumArr(int a[], int n,int* start, int* end) -
{ -
int s, e; -
int sum = a[0]; -
int bMax=a[0]; -
*start = *end = 0; -
for (int i = 1; i < n; i++) -
{ -
if (bMax > 0) //情况一,子数组包含a[i],且b[i-1]>0(上一次的最优解大于0),b[i] = b[i-1]+a[i] -
{ -
bMax += a[i]; -
e = i; -
} -
else //情况二,子数组包含a[i],且b[i-1]<=0(上一次的最优解小于0),这时候以a[i]重新作为b[i]的起点。 -
{ -
bMax = a[i]; -
s = i; -
e = i; -
} //情况三,子数组不包含a[i],即b[i]=sum -
if (bMax > sum) //三种情况相比较,最大值作为更新后的最优解,存在sum -
{ -
sum = bMax; -
*start = s; -
*end = e; -
} -
} -
return sum; -
}
引申:求子数组和的最小值
同理。
-
//求数组的子数组和的最小值,时间复杂度为O(n) -
int minSumArr(int a[], int n, int* start, int* end) -
{ -
int s, e; -
int bMin = a[0]; -
int sum = a[0]; -
*start = *end = 0; -
for (int i = 0; i < n; i++) -
{ -
if (bMin < 0) //情况一,子数组包含a[i], 且b[i-1]<0,b[i] = b[i-1]+a[i] -
{ -
bMin += a[i]; -
e = i; -
} -
else //情况二,子数组包含a[i],且b[i-1] > 0,这时候以a[i]重新作为b[i]的起点 -
{ -
bMin = a[i]; -
s = e = i; -
} //情况三,子数组不包含a[i],即b[i]=sum -
if (bMin < sum) //三种情况相比较,最小值作为更新后的最优解,存在sum -
{ -
sum = bMin; -
*start = s; -
*end = e; -
} -
} -
return sum; -
}
4、给出10W条人和人之间的朋友关系,求出这些朋友关系中有多少个朋友圈(如A-B、B-C、D-E、E-F,这4对关系中存在两个朋友圈),并给出算法的时间复杂度。
-
-
int set[10001]; -
int find(int x) -
{ -
int i, j, r; -
r = x; -
while (set[r] != r) //寻找此集合的代表 -
r = set[r]; -
i = x; -
while (i != r) //使得r代表的集合中,所有结点直接指向r,即路径压缩 -
{ -
j = set[i]; -
set[i] = r; -
i = j; -
} -
return r; -
} -
void merge(int x, int y) -
{ -
int t = find(x); -
int h = find(y); -
if (t < h) -
set[h] = t; -
else -
set[t] = h; -
} -
int friends(int n, int m, int (*r)[2]) //n个人,m对好友关系,存放在二维数组r[m][2]中 -
{ -
int i, count; -
for (i = 1; i <= n; i++) -
set[i] = i; -
for (i = 0; i < m; i++) -
merge(r[i][0], r[i][1]); -
count = 0; -
for (i = 1; i <= n; i++) -
{ -
if (set[i] == i) -
count++; -
} -
return count; -
}
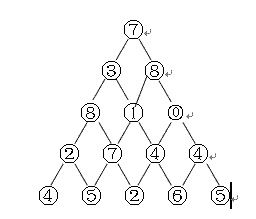
5、如图所示的数字三角形,从顶部出发,在每一结点可以选择向左走或得向右走,一直走到底层,要求找出一条路径,使路径上的值的和最大。给出算法的时间复杂度。
定义状态为:dp[i][j]表示,从第i行第j个数字到最后一行的某个数字的权值最大的和。那么我们最后只需要输出dp[1][1]就是答案了.
状态转移方程为:dp[i][j] += max( dp[i+1][j+1],dp[i+1][j] );好了, 从第n-1行往上面倒退就好了。
6、有一个很长二进制串,求出除以3的余数是多少,给出算法的时间复杂度。