LSTM做回归预测，拟合sin曲线

一些知识点

因为RNN太长会导致反向传播时间长效率低，也可能导致梯度消失等问题，所以一般是这样做的，设定一个参数TIME_STEPS，说明一个RNN网络由多少个时间点组成。再重新说明下概念，一个RNN网络由很多个时间点组成，这里我们的时间点个数为TIME_STEPS，同时，一个时间点有batch_size个单元cell（这个单元可以是最简单的RNN单元，也可以是LSTM单元，也可以是GRU单元），并且，这个单元内有很多隐藏单元（因为输入和传递的隐状态都是向量的形式，所以这个单元内的参数也不只一个，也是一个向量，即隐藏单元）。

关于下面RNN程序的运行过程可以看一下这个博客：https://blog.csdn.net/zgj_gutou/article/details/86524414

在训练的时候，我们取数据一般都取一个batch_size，在这里实际上是取了batch_size*TIME_STEPS个点。

注意程序中l_out_x和Ws_out维度，可以看出cell_size(一个cell中的隐藏单元)可以说是一个中介。

最后的预测结果输出维度是(batch_size*steps, output_size)，是二维的，后面为了计算均方误差，还要用reshape([-1)来转换为一维的向量。（这里的step就是上面说的TIME_STEPS）

程序中有一个地方稍微注意下：

if i == 0:
    feed_dict = {model.xs: seq,model.ys: res,} # create initial state
else:
    feed_dict = {model.xs: seq,model.ys: res,model.cell_init_state: state } # use last state as the initial state for this run

上次的状态输出作为这次的状态输入,注意这里跟用RNN进行图片分类不一样，图片分类中每张照片其实是没有关联的，第一张照片的状态输出跟第二张照片的状态输入是没有关系的。
但这里作为一个回归问题，每个状态的输出都是下一次的状态输入。
可以对比一下这个程序中如果不把前一个状态输出作为下一个状态输出的情况：
下图是把前一个状态输出作为下一个状态输出的情况的图：

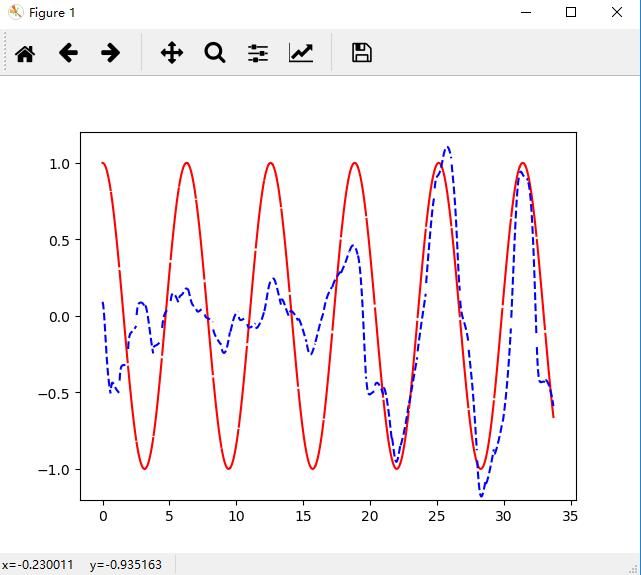
下图是不把前一个状态输出作为下一个状态输出的情况的图，可以看出来确实是断断续续的：

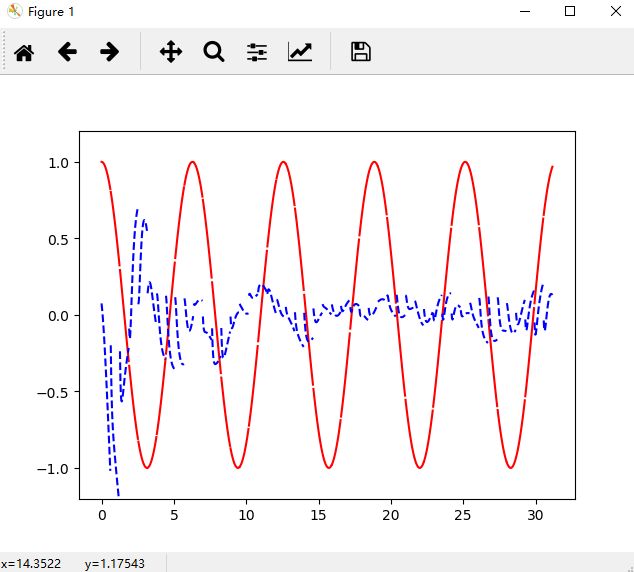
完整的程序(可以直接复制到编译器中运行)

# View more python learning tutorial on my Youtube and Youku channel!!!

# Youtube video tutorial: https://www.youtube.com/channel/UCdyjiB5H8Pu7aDTNVXTTpcg
# Youku video tutorial: http://i.youku.com/pythontutorial

"""
Please note, this code is only for python 3+. If you are using python 2+, please modify the code accordingly.
Run this script on tensorflow r0.10. Errors appear when using lower versions.
"""
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

BATCH_START = 0
TIME_STEPS = 20   # 20个时间点
BATCH_SIZE = 50
INPUT_SIZE = 1  # 一个时间点上对应一个输入
OUTPUT_SIZE = 1  # 一个时间点上对应一个输出
CELL_SIZE = 10   # 也就是一个cell里面有多少个hidden_units
LR = 0.006

def get_batch():
    global BATCH_START, TIME_STEPS
    # xs shape (50batch, 20steps)
    xs = np.arange(BATCH_START, BATCH_START+TIME_STEPS*BATCH_SIZE).reshape((BATCH_SIZE, TIME_STEPS)) / (10*np.pi)
    seq = np.sin(xs)
    res = np.cos(xs)
    BATCH_START += TIME_STEPS
    # plt.plot(xs[0, :], res[0, :], 'r', xs[0, :], seq[0, :], 'b--')
    # plt.show()
    # returned seq, res and xs: shape (batch, step, input)
    return [seq[:, :, np.newaxis], res[:, :, np.newaxis], xs]

class LSTMRNN(object):
    def __init__(self, n_steps, input_size, output_size, cell_size, batch_size):
        self.n_steps = n_steps
        self.input_size = input_size
        self.output_size = output_size
        self.cell_size = cell_size
        self.batch_size = batch_size
        with tf.name_scope('inputs'):
            self.xs = tf.placeholder(tf.float32, [None, n_steps, input_size], name='xs')
            self.ys = tf.placeholder(tf.float32, [None, n_steps, output_size], name='ys')
        with tf.variable_scope('in_hidden'):   # 输入LSTM单元前先进行一个线性变换
            self.add_input_layer()
        with tf.variable_scope('LSTM_cell'):
            self.add_cell()
        with tf.variable_scope('out_hidden'):  # LSTM单元输出后再进行一个线性变换
            self.add_output_layer()
        with tf.name_scope('cost'):  # 计算损失
            self.compute_cost()
        with tf.name_scope('train'):  # 训练优化
            self.train_op = tf.train.AdamOptimizer(LR).minimize(self.cost)

    def add_input_layer(self,):
        l_in_x = tf.reshape(self.xs, [-1, self.input_size], name='2_2D')  # (batch*n_step, in_size)
        # Ws (in_size, cell_size)
        Ws_in = self._weight_variable([self.input_size, self.cell_size]) # cell_size就是隐藏单元个数
        # bs (cell_size, )
        bs_in = self._bias_variable([self.cell_size,])
        # l_in_y = (batch * n_steps, cell_size)
        with tf.name_scope('Wx_plus_b'):
            l_in_y = tf.matmul(l_in_x, Ws_in) + bs_in
        # reshape l_in_y ==> (batch, n_steps, cell_size)
        self.l_in_y = tf.reshape(l_in_y, [-1, self.n_steps, self.cell_size], name='2_3D')

    def add_cell(self):
        lstm_cell = tf.contrib.rnn.BasicLSTMCell(self.cell_size, forget_bias=1.0, state_is_tuple=True)
        with tf.name_scope('initial_state'):
            self.cell_init_state = lstm_cell.zero_state(self.batch_size, dtype=tf.float32)   # cell_init_state维度由batch_size和cell_size决定
        self.cell_outputs, self.cell_final_state = tf.nn.dynamic_rnn(
            lstm_cell, self.l_in_y, initial_state=self.cell_init_state, time_major=False)

    def add_output_layer(self):
        # shape = (batch * steps, cell_size)
        l_out_x = tf.reshape(self.cell_outputs, [-1, self.cell_size], name='2_2D')  # 注意l_out_x和Ws_out维度，可以看出cell_size(一个cell中的隐藏单元)可以说是一个中介
        Ws_out = self._weight_variable([self.cell_size, self.output_size])
        bs_out = self._bias_variable([self.output_size, ])
        # shape = (batch * steps, output_size)
        with tf.name_scope('Wx_plus_b'):
            self.pred = tf.matmul(l_out_x, Ws_out) + bs_out   # pred在这里的维度是(batch_size*steps, output_size),即(50*20,1)

    def compute_cost(self):
        reshape_pred = tf.reshape(self.pred, [-1])   # self.pred的shape是(1000,1),是二维的,reshape之后的shape是(1000)，是一维的
        reshape_target = tf.reshape(self.ys, [-1])
        losses = tf.square(tf.subtract(reshape_pred, reshape_target))  # 平方误差
        with tf.name_scope('average_cost'):   # 均方误差
            self.cost = tf.div(tf.reduce_sum(losses, name='losses_sum'),self.batch_size,name='average_cost')

    def _weight_variable(self, shape, name='weights'):
        initializer = tf.random_normal_initializer(mean=0., stddev=1.,)
        return tf.get_variable(shape=shape, initializer=initializer, name=name)

    def _bias_variable(self, shape, name='biases'):
        initializer = tf.constant_initializer(0.1)
        return tf.get_variable(name=name, shape=shape, initializer=initializer)

if __name__ == '__main__':
    model = LSTMRNN(TIME_STEPS, INPUT_SIZE, OUTPUT_SIZE, CELL_SIZE, BATCH_SIZE)
    sess = tf.Session()
    init = tf.global_variables_initializer()
    sess.run(init)

    plt.ion()
    plt.show()
    for i in range(200):
        seq, res, xs = get_batch()
        # feed_dict = {model.xs: seq, model.ys: res, }
        if i == 0:
            feed_dict = {model.xs: seq,model.ys: res,} # create initial state
        else:
            feed_dict = {model.xs: seq,model.ys: res,model.cell_init_state: state } # use last state as the initial state for this run
            # 上次的状态输出作为这次的状态输入,注意这里跟用RNN进行图片分类不一样，图片分类中每张照片其实是没有关联的，第一张照片的状态输出跟第二张照片的状态输入是没有关系的
            # 但这里作为一个回归问题，每个状态的输出都是下一次的状态输入
        _, cost, state, pred = sess.run([model.train_op, model.cost, model.cell_final_state, model.pred],feed_dict=feed_dict)
        if i % 20 == 0:
            print('cost: ', round(cost, 4))
        # plotting
        plt.plot(xs[0, :], res[0].flatten(), 'r', xs[0, :], pred.flatten()[:TIME_STEPS], 'b--')
        plt.ylim((-1.2, 1.2))
        plt.draw()
        plt.pause(0.3)

输出结果如下：

cost:  31.1363
cost:  9.1072
cost:  5.8087
cost:  1.8695
cost:  0.3018
cost:  0.6436
cost:  0.2898
cost:  0.3421
cost:  0.1882
cost:  0.0433

参考网址：https://morvanzhou.github.io/tutorials/machine-learning/tensorflow/5-09-RNN3/ 感谢！
参考网址：https://r2rt.com/styles-of-truncated-backpropagation.html 感谢！