深度残差网络 ResNet

作为 CVPR2016 的 best paper，何凯明的文章【1】针对深层网络梯度弥散导致的SGD优化难题，提出了 residual（残差）结构，很好的解决了模型退化问题，在50层、101层、152层甚至1202层的网络上测试均获得了很好的效果。

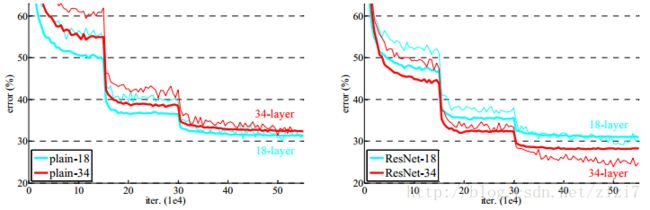
应用了ResNet的错误率大大低于其他主流深度网络（图1）

　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　图1.ResNet网络在 ImageNet15上获得冠军

---

网络模型

一个很显然的事实是：越深的网络表达能力越强。但随着深度的提高，梯度弥散的现象越明显，导致SGD无法收敛，最终精度反而下降（图2）

　　　　　　　　　　　　　　　
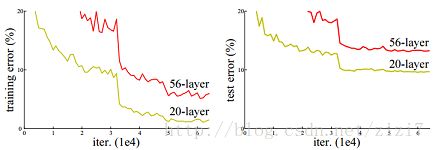
　　　　　　　　　　　　　　　　　图2. 常规56层网络无论训练还是测试，精度都比20层网络差

针对该问题，方法提出一个 Residual（残差）结构，对于1000多层的网络也能保持很好的训练效果（虽然此时已经出现了过拟）

　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　图3. 残差结构直接将输入 x 接入输出，相当于引入了一个恒等映射

如图3所示，假设原始网络要学的函数为 H(x) ，作者将其分解为 H(x)=F(x)+x 。
分解后原始网络（图3垂直向下的流程）拟合 F(x) ，盘支（图3弯曲的 shortcut connection）

图4为 VGG-19、34层普通网络和34层添加残差的网络结构

　　　　　　　　　　　　　　　　　　
　　　　　　　　　　图4. 相较于普通网络，ResNet 只需增加 shortcut connection（虚线是将通道数乘以2）

作者的实验表明，残差结构需要2层以上才会有效果，如下式中 Ws 表示的线性变换也仅是统一输入输出的维度，对训练效果提升没有帮助

y=F(x,Wi)+Wsx

图5是作者使用 ResNet 的实验效果

　　　　　　　
　　　　　　　　　　　　　　　　　　　　　图5. ResNet网络（右）与普通网络（左）的训练误差

---

为什么 ResNet 起作用

这里需要回答两个问题：

• 一是为什么分解为 H(x)=F(x)+x （实际优化的是 F(x)=0 ）；
• 二是为什么分解后能解决梯度涣散的问题

对于第一个问题，作者并没有从原理上做解释，而是通过实验证明其是最优的。知乎上关于为什么用 x 而不是 0.5x 或者其他的一个回答是：“实践发现机器学习要拟合的（target function）函数 f(x) 经常是很接近同一映射函数的。”但我不能理解。

对于第二个问题，有以下3种解释：
1）由于网络权重初始值往往在0附近，因此优化 F(x)=0 是有天然优势的。
　　一个比喻是：假设要拟合的函数是一根直线（在这里就是 H(x) ），那么用一根直线（残差结构 x ）和一些微小的折线（ F(x) ）来叠加肯定比单纯的用直线或者折线拟合要容易优化的多

2）比如把 5 映射到 5.1
　　如果普通网络，则是 F′(5)=5.1
　　引入残差后为 H(5)=5.1 ， H(5)=F(5)+5 ，那么 F(5)=0.1
　　可以看到，普通网络输入输出的“梯度”仅为2%，而残差网络的映射 F 增加了100%

3）这篇文章从另一个角度理解残差：将其看做一个投票系统

　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　图6. 残差网络可以分解为多钟路径组合的网络

如图6所示，残差网络其实是很多并行子网络的组合。因此虽然表面上看 ResNet 可以做到很深，但这个组合里大部分网络路径其实都几种在中间的路径长度上。

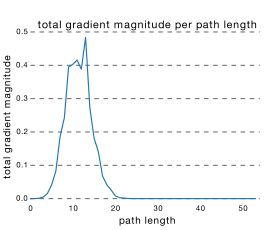
图7通过各个路径长度上包含的网络数乘以每个路径的梯度值，统计了 ResNet 真正起作用的路径

　　　　　　　　　　　　　　　　 　　　
　　　　　　　　　　　　　　　　　　　　　图7. 真正起作用的路径长度不到20层

因此，“ResNet 只是表面上看起来很深，事实上网络却很浅”。“ResNet 没有真的解决深度网络的梯度涣散问题，其实质就是一个多人投票系统”。

---

代码实现

作者在 github 上放出了 caffe 下的网络模型，并且介绍了第三方在其他平台的实现

---

【1】He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

---