有向无环图DAG 拓扑排序 代码解释
目录:
- DAG定义
- 举例描述
- 实际运用
- 算法描述
- 算法实战
- 算法可视化
定义
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序(英语:Topological sorting)。
- 每个顶点出现且只出现一次;
- 若A在序列中排在B的前面,则在图中不存在从B到A的路径。
也可以定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得如果存在一条从顶点A到顶点B的路径,那么在排序中B出现在A的后面。
或者
有向无环图(Directed Acyclic Graph, DAG)是有向图的一种,字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系,管理任务之间的调度。拓扑排序是对DAG的顶点进行排序,使得对每一条有向边(u, v),均有u(在排序记录中)比v先出现。亦可理解为对某点v而言,只有当v的所有源点均出现了,v才能出现。
需要记住的英语单词:
E: edge 边
V: vertex 顶点
常会看到(E, V)描述
举例描述
有向无环图的拓扑排序:
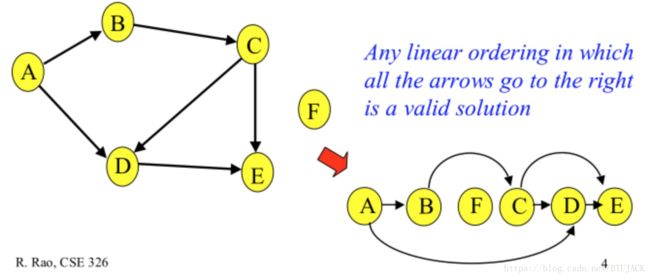
正面例子
左侧是有向无环图,右侧是拓扑排序后的队列。在右侧队列中,沿着箭头方向的任意线性顺序在左侧图中都有对应的路线,此时,我们才能说右侧的拓扑排序是成功的排序。
注意:一个图可以有很多种或者没有一种拓扑排序序列 (n >= 0)
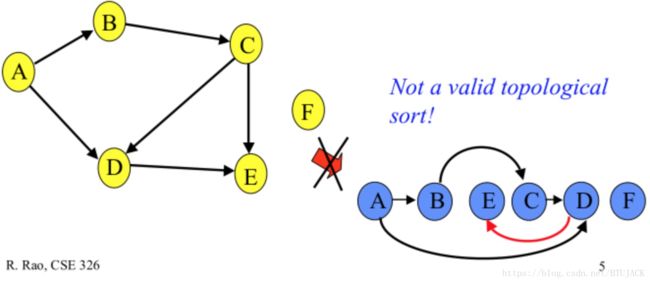
反面例子
非法拓扑排序,因为D比E后出现了。
强调:拓扑排序后的序列要保证所有箭头方向路线在图中都有对应路线才能说拓扑排序正确
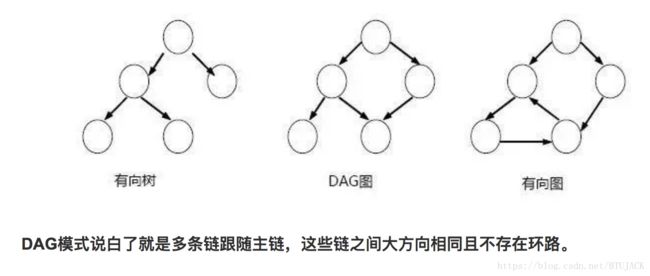
有向树,有向无环图,无向图对比
实际运用
拓扑排序 Topological Sorting 是一个经典的图论问题。他实际的运用中,拓扑排序可以做如下的一些事情:
- 检测编译时的循环依赖
- 制定有依赖关系的任务的执行顺序
拓扑排序不是一种排序算法
虽然名字里有 Sorting,但是相比起我们熟知的 Bubble Sort, Quick Sort 等算法,Topological Sorting 并不是一种严格意义上的 Sorting Algorithm。
确切的说,一张图的拓扑序列可以有很多个,也可能没有。拓扑排序只需要找到其中一个序列,无需找到所有序列。
算法描述:
入度与出度
在介绍算法之前,我们先介绍图论中的一个基本概念,入度和出度,英文为 in-degree & out-degree。
在有向图中,如果存在一条有向边 A-->B,那么我们认为这条边为 A 增加了一个出度,为 B 增加了一个入度。
算法流程
拓扑排序的算法是典型的宽度优先搜索算法,其大致流程如下:
- 统计所有点的入度,并初始化拓扑序列为空。
- 将所有入度为 0 的点,也就是那些没有任何
依赖的点,放到宽度优先搜索的队列中 - 将队列中的点一个一个的释放出来,放到拓扑序列中,每次释放出某个点 A 的时候,就访问 A 的相邻点(所有A指向的点),并把这些点的入度减去 1。
- 如果发现某个点的入度被减去 1 之后变成了 0,则放入队列中。
- 直到队列为空时,算法结束,
算法实战:
用lintcode真题实战巩固此算法:
题目描述:
615. 课程表
现在你总共有 n 门课需要选,记为 0 到 n - 1.
一些课程在修之前需要先修另外的一些课程,比如要学习课程 0 你需要先学习课程 1 ,表示为[0,1]
给定n门课以及他们的先决条件,判断是否可能完成所有课程?
样例
给定 n = 2,先决条件为 [[1,0]] 返回 true
给定 n = 2,先决条件为 [[1,0],[0,1]] 返回 false
代码实现:
#采用拓扑排序方法
from queue import Queue
class Solution:
# @param {int} numCourses a total of n courses
# @param {int[][]} prerequisites a list of prerequisite pairs
# @return {boolean} true if can finish all courses or false
def canFinish(self, numCourses, prerequisites):
# Write your code here
edges = {i: [] for i in range(numCourses)} #边,建立一个空字典{0: [], 1: [], 2: []};初始化拓扑排序序列为空
degrees = [0 for i in range(numCourses)] #入度,出度的个数;[0, 0, 0, 0, 0, 0]
for i, j in prerequisites:
edges[j].append(i)
degrees[i] += 1
#import Queue
queue, count = Queue(maxsize = numCourses), 0 # | Create a queue object with a given maximum size.
for i in range(numCourses):
if degrees[i] == 0: #入度为零的点放到宽度优先搜索的队列中
queue.put(i) # | Put an item into the queue.
while not queue.empty(): #直到队列为空时候,算法结束
node = queue.get() # 把队列queue中的点释放出来,放到拓扑中去。| Remove and return an item from the queue.
count += 1
for x in edges[node]: #每次释放出点A的时候,就访问A的相邻点。
degrees[x] -= 1 #并把这些点的入度减一
if degrees[x] == 0: #如果发现某个点的入度减一变为0后,就把他放入队列queue中
queue.put(x)
return count == numCourses
my_solution = Solution()
data = [[1,0],[0,1]]
n = 2
order = my_solution.canFinish(n, data) #打印二叉树分层遍历结果;levelOrder括号里面是root,但是我这里放入的是整个二叉树,怎么就没有报错
print(order)
lintcode实战2:
127. 拓扑排序
给定一个有向图,图节点的拓扑排序定义如下:
对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
针对给定的有向图找到任意一种拓扑排序的顺序.
样例
例如以下的图:
picture
拓扑排序可以为:
[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]
挑战
能否分别用BFS和DFS完成?
用BFS算法实现:
"""
Definition for a Directed graph node
class DirectedGraphNode:
def __init__(self, x):
self.label = x
self.neighbors = []
"""
class Solution:
"""
@param graph: A list of Directed graph node
@return: A list of integer
"""
def topSort(self, graph):
node_to_indegree = self.get_indegree(graph)
# bfs
order = [] #拓扑序列
start_nodes = [n for n in graph if node_to_indegree[n] == 0] #找到入度为0的节点
queue = collections.deque(start_nodes) #将所有入度为 0 的点,也就是那些没有任何依赖的点,放到宽度优先搜索的队列中
while queue:
node = queue.popleft() #将队列中的点一个一个的释放出来
order.append(node) #,放到拓扑序列中
for neighbor in node.neighbors: #每次释放出某个点 A 的时候,就访问 A 的相邻点(所有A指向的点),并把这些点的入度减去 1。
node_to_indegree[neighbor] -= 1 #并把这些点的入度减去 1。
if node_to_indegree[neighbor] == 0: #如果发现某个点的入度被减去 1 之后变成了 0,则放入队列中。
queue.append(neighbor)
return order #整个算法的出口,返回一个序列,这个序列人看不到,只有机器能看懂
def get_indegree(self, graph): #返回一个字典,字典的key是graph里的节点,key对应的值为节点的入度
node_to_indegree = {x: 0 for x in graph} #建立空字典,图里每个节点的值都是0,x 就是图中的节点;统计所有点的入度,并初始化拓扑序列为空。
for node in graph: #D指向E,E没有指向D,所以,E是D的邻居,D不是E的邻居
for neighbor in node.neighbors: #node.neighbors:就是节点A的所有相邻点。然后取每一个邻居neighbor;A 的相邻点:所有A指向的点,不包括指向A的点
node_to_indegree[neighbor] += 1 #然后它的每个邻居indegree加一;这里的邻居其实特指出度的邻居,比如D指向E,E自动加一。并不是所有邻居那个概念
return node_to_indegree
用DFS算法实现:(不推荐面试的时候用)
"""
Definition for a Directed graph node
class DirectedGraphNode:
def __init__(self, x):
self.label = x
self.neighbors = []
"""
class Solution:
"""
@param graph: A list of Directed graph node
@return: A list of integer
"""
def topSort(self, graph):
indegree = {}
for x in graph:
indegree[x] = 0
for i in graph:
for j in i.neighbors:
indegree[j] += 1
ans = []
for i in graph:
if indegree[i] == 0:
self.dfs(i, indegree, ans)
return ans
def dfs(self, i, indegree, ans):
ans.append(i)
indegree[i] -= 1
for j in i.neighbors:
indegree[j] -= 1
if indegree[j] == 0:
self.dfs(j, indegree, ans)
算法可视化:
BFS实现拓扑排序可视化:
https://www.cs.usfca.edu/~galles/visualization/TopoSortIndegree.html
深度优先搜索的拓扑排序
深度优先搜索也可以做拓扑排序,不过因为不容易理解,也并不推荐作为拓扑排序的主流算法。
DFS实现拓扑排序可视化:
https://www.cs.usfca.edu/~galles/visualization/TopoSortDFS.html
认识你是我们的缘分,同学,等等,记得关注我。
微信扫一扫
关注该公众号