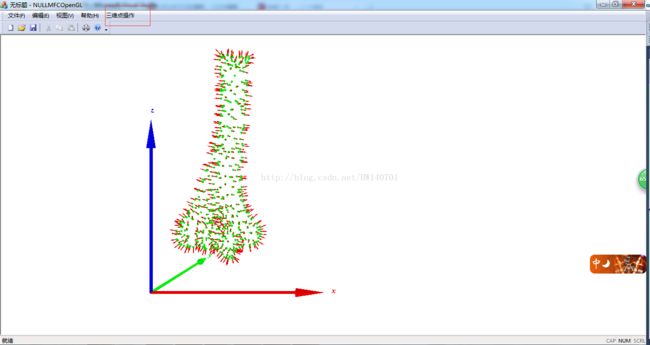
OpenGL+MFC对三维点云的法向量实现可视化
最近有小伙伴在问,我想显示一个求得的三维点云中的每一个点的法向量的指向,怎么获得这种逼真的三维显示效果呢?当然是OpenGL啦,也是我自己用的比较习惯,所以就花了十几分钟帮助上面提问的小伙伴解决问题,然后也提供给大家一个查看三维点云法向量的工具,稍后我会在我的CSDN的下载频道上传该软件的Release版本供大家使用,主要的显示效果是三维点云中的每一个点使用实心球体表示,法向量用一个方向箭头和圆锥体表示,类似于坐标轴的指向。主要用到三个函数,Render3DCylinder(在任意两个三维点间画圆柱体),Render3DSphere(以任意三维点为中心画球体),Render3DCone(在任意两个三维点之间画圆锥体)。
其三个函数的主要代码如下:
/*-----Render3DCylinder()-------------------------------------------------
函数功能:在任意两个三维点之间绘制给定半径的圆柱体管道
函数参数:m_point1为第一个三维点
m_point2为第二个三维点
radius为圆柱体半径
slices为段数,slices围绕着z轴分片的个数。
stacks为递归次数,stacks顺着z轴分片的个数。stacks和slices垂直。
slices和stacks设置的越大,占的内存就越多,这里设置slices为15,stacks为1
------------------------------------------------------------------------*/
Render3DCylinder(My3DPoint &m_point1,My3DPoint &m_point2,double radius,double slices,double stacks)
{
//计算目标向量
GLdouble dir_x = m_point2.X-m_point1.X;
GLdouble dir_y = m_point2.Y-m_point1.Y;
GLdouble dir_z = m_point2.Z-m_point1.Z;
//算出目标向量模
GLdouble bone_length = sqrt( dir_x*dir_x + dir_y*dir_y + dir_z*dir_z );
GLUquadricObj * quad_obj = NULL;
if ( quad_obj == NULL )
quad_obj = gluNewQuadric();
gluQuadricDrawStyle(quad_obj, GLU_FILL );
gluQuadricNormals(quad_obj, GLU_SMOOTH );
glPushMatrix();
// 平移到起始点
glTranslated( m_point1.X, m_point1.Y, m_point1.Z );
// 计算长度
double length;
length = sqrt( dir_x*dir_x + dir_y*dir_y + dir_z*dir_z );
if ( length < 0.0001 ) {
dir_x = 0.0; dir_y = 0.0; dir_z = 1.0; length = 1.0;
}
dir_x /= length; dir_y /= length; dir_z /= length;
// 计算起始向量
GLdouble up_x, up_y, up_z;
up_x = 0.0;
up_y = 1.0;
up_z = 0.0;
// 计算向量(dir_x,dir_y,dir_z)与向量(up_x,up_y,up_z)的法向量(side_x ,side_y,side_z)
double side_x, side_y, side_z;
side_x = up_y * dir_z - up_z * dir_y;
side_y = up_z * dir_x - up_x * dir_z;
side_z = up_x * dir_y - up_y * dir_x;
length = sqrt( side_x*side_x + side_y*side_y + side_z*side_z );
if ( length < 0.0001 ) {
side_x = 1.0; side_y = 0.0; side_z = 0.0; length = 1.0;
}
side_x /= length; side_y /= length; side_z /= length;
up_x = dir_y * side_z - dir_z * side_y;
up_y = dir_z * side_x - dir_x * side_z;
up_z = dir_x * side_y - dir_y * side_x;
// 计算变换矩阵
GLdouble m[16] = { side_x, side_y, side_z, 0.0,
up_x, up_y, up_z, 0.0,
dir_x, dir_y, dir_z, 0.0,
0.0, 0.0, 0.0, 1.0 };
glMultMatrixd( m );
// 圆柱体参数
GLdouble radius1= radius; // 半径
GLdouble slices1 = slices; // 段数
GLdouble stack1 = stacks; // 递归次数
gluCylinder(quad_obj,radius1,radius,bone_length,slices1,stack1);
glPopMatrix();
gluDeleteQuadric(quad_obj);//销毁二次方程对象,释放内存
}/*-----Render3DCone()-------------------------------------------------
函数功能:在任意两个三维点之间绘制给定半径的三维圆锥体
函数参数:m_point1为第一个三维点
m_point2为第二个三维点
radius为圆柱体半径
slices为段数,slices围绕着z轴分片的个数。
stacks为递归次数,stacks顺着z轴分片的个数。stacks和slices垂直。
slices和stacks设置的越大,占的内存就越多,这里设置slices为15,stacks为1
------------------------------------------------------------------------*/
Render3DCone(My3DPoint &m_point1,My3DPoint &m_point2,double radius,double slices,double stacks)
{
//计算目标向量
GLdouble dir_x = m_point2.X-m_point1.X;
GLdouble dir_y = m_point2.Y-m_point1.Y;
GLdouble dir_z = m_point2.Z-m_point1.Z;
//算出目标向量模
GLdouble bone_length = sqrt( dir_x*dir_x + dir_y*dir_y + dir_z*dir_z );
GLUquadricObj * quad_obj = NULL;
if ( quad_obj == NULL )
quad_obj = gluNewQuadric();
gluQuadricDrawStyle(quad_obj, GLU_FILL );
gluQuadricNormals(quad_obj, GLU_SMOOTH );
glPushMatrix();
// 平移到起始点
glTranslated( m_point1.X, m_point1.Y, m_point1.Z );
// 计算长度
double length;
length = sqrt( dir_x*dir_x + dir_y*dir_y + dir_z*dir_z );
if ( length < 0.0001 ) {
dir_x = 0.0; dir_y = 0.0; dir_z = 1.0; length = 1.0;
}
dir_x /= length; dir_y /= length; dir_z /= length;
// 计算起始向量
GLdouble up_x, up_y, up_z;
up_x = 0.0;
up_y = 1.0;
up_z = 0.0;
// 计算向量(dir_x,dir_y,dir_z)与向量(up_x,up_y,up_z)的法向量(side_x ,side_y,side_z)
double side_x, side_y, side_z;
side_x = up_y * dir_z - up_z * dir_y;
side_y = up_z * dir_x - up_x * dir_z;
side_z = up_x * dir_y - up_y * dir_x;
length = sqrt( side_x*side_x + side_y*side_y + side_z*side_z );
if ( length < 0.0001 ) {
side_x = 1.0; side_y = 0.0; side_z = 0.0; length = 1.0;
}
side_x /= length; side_y /= length; side_z /= length;
up_x = dir_y * side_z - dir_z * side_y;
up_y = dir_z * side_x - dir_x * side_z;
up_z = dir_x * side_y - dir_y * side_x;
// 计算变换矩阵
GLdouble m[16] = { side_x, side_y, side_z, 0.0,
up_x, up_y, up_z, 0.0,
dir_x, dir_y, dir_z, 0.0,
0.0, 0.0, 0.0, 1.0 };
glMultMatrixd( m );
// 圆柱体参数
GLdouble radius1= radius; // 半径
GLdouble slices1 = slices; // 段数
GLdouble stack1 = stacks; // 递归次数
gluCylinder(quad_obj,radius1,0.0,bone_length,slices1,stack1);
glPopMatrix();
gluDeleteQuadric(quad_obj);//销毁二次方程对象,释放内存
}/*-----Render3DSphere()-------------------------------------------------
函数功能:在任意点绘制任意半径的球体
函数参数:
qiuxin为My3DPoint结构,存储着球心的XYZ的坐标值
radius为圆柱体半径
slices为段数,slices围绕着z轴分片的个数。
stacks为递归次数,stacks顺着z轴分片的个数。stacks和slices垂直。
slices和stacks设置的越大,占的内存就越多,这里设置slices为15,stacks为1
------------------------------------------------------------------------*/
Render3DSphere(My3DPoint &qiuxin,double radius,double slices,double stacks)
{
GLUquadricObj * quad_obj = NULL;
if ( quad_obj == NULL )
quad_obj = gluNewQuadric();
gluQuadricDrawStyle(quad_obj, GLU_FILL );
gluQuadricNormals(quad_obj, GLU_SMOOTH );
glPushMatrix();
// 平移到起始点
glTranslated( qiuxin.X, qiuxin.Y, qiuxin.Z );
gluSphere(quad_obj,radius,slices,stacks);
glPopMatrix();
gluDeleteQuadric(quad_obj);//销毁二次方程对象,释放内存
}整个程序的源码由于项目的关系不能给出,只能给出发布版本,不过主要的核心的功能是利用上述的三个函数实现的。相应的程序的Realease版本的下载地址:[免费]OpenGL+MFC显示三维点云中每一个点的法向量,Release版本-CSDN下载 http://download.csdn.net/download/hw140701/9970732http://download.csdn.net/download/hw140701/9970732