从最大子数组和问题详尽贪心算法策略

问题：给定数组 a[1,2..n] ，求最大子数组和，即找出 1≤i≤j≤n 使得 a[i]+a[i]+..+a[j] 值最大。

有三种方法可以解决上述问题：
第一种 ：暴力枚举法，其时间复杂度为 O(n3)
第二种 ：优化枚举法，其时间复杂度为 O(n2)
第三种 ：贪心方法，其时间复杂度为 O(n)

以上三种方法，暴力枚举是一种万能的算法，但不是对于任何问题都适用，优化枚举是一种较为优化的算法，贪心算法则是本题的最优解。如果一个问题，你给出的算法时间复杂度为 O(n3) ， O(n2) ， O(2n) ， O(n！) 我们需要注意两点.
1. 明确数据量的大小.
2. 可能会有更优化的方法.

谈算法不谈时间复杂度等于耍流氓，本题是一道经典的算法题，前两种方法比较好理解。下面我们给出详细思路：

方法一：

暴力枚举法：
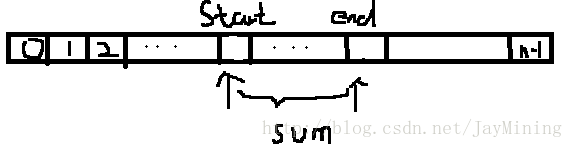
    包括三层循环，首先定义一个数组nums，第一层循环从数组头0 遍历每个位置 start 作为子数组起始索引，第二层循环，从 start 处遍历 大于等于 start 的位置 end ,最后一层对于 start，end 之间的每个元素，遍历并累加起来得到 Sum[start,end]
示意图如下：

以下是暴力枚举的代码：

public static int maxSubArray1(int[] nums) {
        int n=nums.length;
        //设定 sum最小值，这里 -2147483647 是int 在java中的最小值
        int sum =-2147483647;    
        //第一层循环，遍历start，也就是子数组的起始索引
        for (int start=0;start//第二层循环，遍历end，也就是子数组结束索引
            for(int end=start;endint ans=0;
                // 得到start,end 以后，将start和end之间的数字加起来
                for (int k=start;k<=end;k++)
                    ans=ans+nums[k];
                if(sum//得到最大的和
                    sum=ans;
            }  
        }
      return sum;
    }

容易理解，很显然 三层循环 ，时间复杂度为 O(n3) ，附加空间复杂度为 O(1)

方法二：

优化枚举法：
     很显然暴力枚举方法并不是很好的一种算法，时间开销很大，如果最大允许一亿次运算，那么数组大小大于1000，该算法就不适用了。下面我们介绍对暴力枚举方法的一种优化。
     容易知道多层循环中的最内层循环是执行最多的，优化枚举就是对最内层循环进行优化，这是一种去冗余思想，很常用。我们知道:
Sum[start,end+1]=Sum[start,end]+num[end+1]
,所以最内层循环并不需要，只需要上一次计算的结果再加一位 num[end+1] 就可以了

因此代码可以优化为：

public static int maxSubArray2(int[] nums) {
        int n=nums.length;
        //设定 sum最小值，这里 -2147483647 是int 在java中的最小值
        int sum =-2147483647;    
        //第一层循环，遍历start，也就是子数组的起始索引
        for (int start=0;startint ans=0; //代码变动地方
              //第二层循环，遍历end，也就是子数组结束索引
            for(int end=start;end/* 得到start,end 以后，将start和end之间的数字加起来,这里只需将上一次的结果加上最后一个num[end]即可*/
                ans=ans+nums[end];
                if(sum//得到最大的和
                    sum=ans;
            }  
        }
      return sum;
    }

可以看出最内层循环被去掉了，因此时间复杂度为 O(n2) ，附加空间复杂度仍然为 O(1)

方法三：

贪心算法：
     虽然本题的时间复杂度已经被降为 O(n2) ，但仍然有最优算法可以解决该问题。可以将本题的时间复杂度降为 O(n) ,首先要转换问题的思考方式：
我们得到的 子数组和使用的是加法，我们可以换一种思路，运用减法方式。

首先定义累加数组 s ，其构造过程时间是一个 O(n) ，只需要遍历一遍一组数组即可得到 :
s[i]=nums[0]+nums[1]+..+nums[i]=s[i−1]+nums[i] ,
那么 Sum[start,end]=s[end]−s[start]

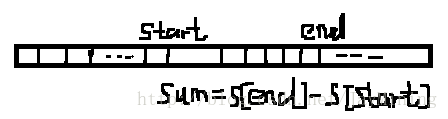
下面这个问题可以转换成，固定 s[end] ，只需要找到最小的 s[start] ，我们记作 minSstart ，实际上，对于每一个位置end，应该都对应一个 minSstart ，所以理论上 minSstart 是 类似于 s 一个数组，其构造过程也是一个 O(n) ,类似的，为了便于理解，给出一个数学公式
minSstart[i]=min(minSstart[i−1],s[i])
表示取 minSstart[i−1],s[i] 中的最小值，因此构造其时间复杂度为 O(n)
一般思想这是一个二重循环，遍历 s 中的 end 位，再遍历 s 中的 start 位，但是大家仔细想一下，这个过程，我们只需要构造出 s和minSstart 就可以了，而这个过程计算与优化枚举sum的计算策略一模一样，我们把以上三个公式单独提出来，大家想一下，结合代码，应该可以理解：
- 优化枚举中 sum 的构造： Sum[start,end+1]=Sum[start,end]+num[end+1]
- s 的构造： s[i]=nums[0]+nums[1]+..+nums[i]=s[i−1]+nums[i]
- minSstart[i] 的构造 minSstart[i]=min(minSstart[i−1],s[i])
可以看出，这种数学规律是，后一次的计算结果，是在前一次的基础上得出的。

下面给出代码，大家仔细体会，虽然比较难理解，但是比一般算法书上的写法，已经有了较大的改变。

    public static int maxSubArray3(int[] nums) {
        int n = nums.length;
            int sum =-2147483647;
            /* sstart ，send 分别表示累加数组的start位和end位 
            也相当于sstart 是前一次计算结果，send是后一次计算结果这里代码中潜在的关系是
            send=sstart+nums[j]
           minSstart 表示最小的minSstart */
            int sstart=0;
            int send=0;
            int minSstart=0;
            for ( int end = 0 ; end< n ; end++){
                /*相当于构建累加数组 s 过程s[j]=s[j-1]+nums[j] 
                好比是后一次结果由前一次结果决定，
                与优化枚举 的优化过程类似ans=ans+nums[end];*/
                send = send + nums[end] ;
                //寻找最小sstart 过程，这一步，minSstart[j]=min(minSstart[j-1],s[j])
                if ( sstart < minSstart ){
                    minSstart=sstart;
                }
                // 更新sum
                 if ( sstart+nums[end]- minSstart >sum){
                    sum =send - minSstart;
                 }
                sstart = sstart + nums[end];
             }
             return sum;
    }

可以看出时间复杂度为 O(n) ，附加空间复杂度为 O(1)

好了，这就是贪心算法的真面目，实际上就是去除代码冗余，发现潜在的代码规律！很明显贪心算法是正确的，希望对大家有用。