EMD学习笔记

参考论文：A_Metric_for_Distributions_with_Applications_to_Image_Databases

论文摘要

在两个分布之间，我们引入了一个的新的距离，称之为土堆移动距离（EMD）。它反映的是，通过移动“分布质量”的方式，把一个分布转换为另一个分布所需要的最小工作量

这是线性优化中运输问题的特殊情况，该问题有高效率的可用算法。EMD算法也允许做局部匹配。当用于比较的分布具有相同的总质量时，EMD是一个确切的度量，并具有易于计算的下界。在本文中，我们重点 在应用程序的图像数据库，特别是彩色和纹理。我们使用EMD，通过多维度展示手段来表现颜色分布和纹理空间的结构。我们还提出了一个关于导航问题的通过一个彩色图片的集合的新方法，这在图像数据库搜索中引出了一个新范例。

 

算法分析

1前言

       EMD算法的算法是基于线性优化中运输问题的求解。从算法来看与运输问题的解法表上作业法相似。但在一些地方有些不同。总体的思路基本一致。

（1）    得到问题，建立模型

（2）    得到初始可行方案

（3）    最优检验

（4）    方案调整

（5）    重复（2）（3）直至方案最优，或者达到最大迭代次数

（6）    输出结果

 

2得到问题，建立模型

      这里体现在算法的输入，是一个具体的问题。具体的操作是构造两个signature。代码相关的定义如下：

typedef struct 
{ 
	int X,Y,Z;; 
} feature_t;

typedef struct
{
  int n;
  feature_t *Features;
  float *Weights;
} signature_t;

其中，feature_t的定义根据实际要求定义，signature_t即为论文提及的签名，定义如上。根据上述定义，可以得到一个简单的exampl.c

#include 
#include 

#include "emd.h"

float dist(feature_t *F1, feature_t *F2)
{
  int dX = F1->X - F2->X, dY = F1->Y - F2->Y, dZ = F1->Z - F2->Z;
  return sqrt((double)dX*dX + dY*dY + dZ*dZ); 
}

main()
{
  feature_t   f1[4] = { {100,40,22}, {211,20,2}, {32,190,150}, {2,100,100} },
	      f2[3] = { {0,0,0}, {50,100,80}, {255,255,255} };
  float       w1[5] = { 0.4, 0.3, 0.2, 0.1 },
              w2[3] = { 0.5, 0.3, 0.2 };
  signature_t s1 = { 4, f1, w1},
	      s2 = { 3, f2, w2};
  float       e;

  e = emd(&s1, &s2, dist, 0, 0);

  printf("emd=%f\n", e);
  getchar();
}

其中，函数dist根据feature_t的定义来编写。其计算的是两两feature_t的G距离，在上述例子中，由于定义的feature_t的定义包含X，Y，Z，所以一个feature_t可以当成是一个点(X,Y,Z)，可以看到，例子中的dist函数即是计算欧式距离。

       事实上，该算法在进行计算的时候，只有所得欧式距离和权重有用。所以无论如何定义feature_t，只要给出了对应dist函数的编写即可。

       调用emd函数，开始计算emd。

 

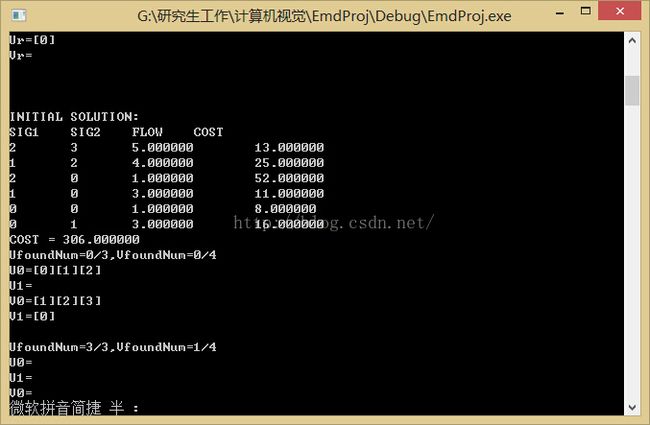
3得到初始方案

       emd函数接收从example.c传来的数据。首先便进行初始化。初始化函数static floatinit()的主要作用有：

（1）    构造了_C[][]二维数组，_C[i][j]为第一个签名中第i个特征与第二个签名中第j个特征的G距离。

（2）    内部函数russel()构造了一个初始可行方案，该函数构造了_X[]数组，该数组保存了方案的每个基变量以及一些辅助信息。

（3）    构造了_IsX[][]二维数组，_IsX[i][j] = 1时，表明第一个签名中第i个特征与第二个签名中第j个特征对应起来了。

 

4检验最优

       检验最优时，算法使用了findBasicVariables()和isOptimal ()两个函数。算法检验最优的方法为表上作业法的位势法。最后所有检验数都为非负数时，方案为最优。

       算法中，函数findBasicVariables()是一个求解方程的过程。最终得到U数组和V数组。而U[i]+V[j]即为对应位置的位势值。

       检验数的值 = _C[i][j] - U[i] - V[j]。基变量的检验数为零。所以，使用一次遍历找到了检验数的最小值，再判断其与0的大小关系，从而来判断是否为最优解。

 

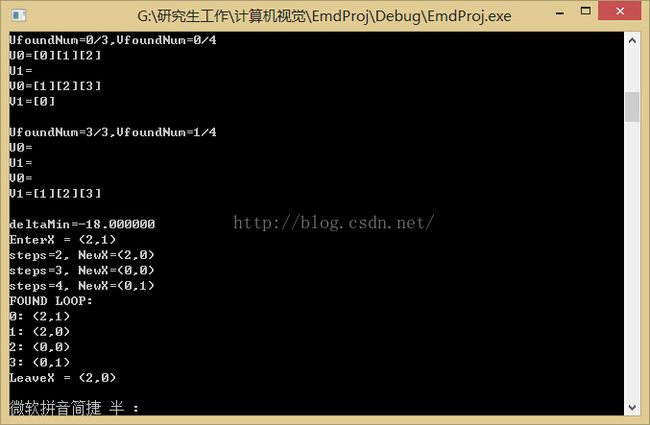
5方案调整

      若当前方案不是最优方案，则需要进行调整。算法所使用的方法为表上作业法的闭回路法。即在最小的检验数的位置，令其为新的基变量。在检验最优时已经找到了该位置。

       然后从该新的基变量出发找到一个闭合回路。该回路是存在且唯一的。利用_X数组中所保存的辅助信息可以找到回路。

       找到回路后，给予新的基变量的位置尽可能大的值。并更新回路。即可得到新方案。

 

6迭代重复、输出结果

       得到新方案后，再次进行检验，直到得到最优解。或达到最大迭代数为止。最后输出结果，emd =cost/w

7程序运行展示