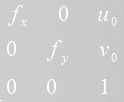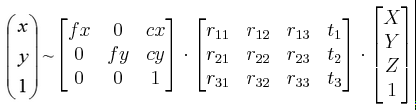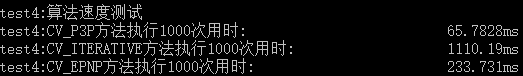【计算机视觉】opencv靶标相机姿态解算2 根据四个特征点估计相机姿态 及 实时位姿估计与三维重建相机姿态

1 基本原理之如何解PNP问题

转载 基本原理之如何解PNP问题

http://www.cnblogs.com/singlex/p/pose_estimation_0.html

相机位姿估计0：基本原理之如何解PNP问题

关键词：相机位姿估计 PNP问题求解

用途：各种位姿估计

文章类型：原理

@Author：VShawn([email protected])

@Date:2016-11-18

@Lab: CvLab202@CSU

 

目录

• 《相机位姿估计0：基本原理之如何解PNP问题》
• 《相机位姿估计1：根据四个特征点估计相机姿态》
• 《相机位姿估计1_1：OpenCV:solvePnP二次封装与性能测试》
• 《相机位姿估计2：[应用]实时位姿估计与三维重建相机姿态》
• 《相机位姿估计3：根据两幅图像的位姿估计结果求某点的世界坐标》

今天给大家讲一讲相机位姿估计的基本原理，说实话我本人也没太了解，这里权当做抛砖引玉了。本来我这个博客是写应用型文章的，但虽然不做理论研究，但你要使用别人的方法来解决问题，那么也还是多多少少要对它的原理有点了解的。

关于PNP问题就是指通过世界中的N个特征点与图像成像中的N个像点，计算出其投影关系，从而获得相机或物体位姿的问题。

 

以下讨论中设相机位于点Oc，P1、P2、P3……为特征点。

 

Case1：当N=1时

当只有一个特征点P1，我们假设它就在图像的正中央，那么显然向量OcP1就是相机坐标系中的Z轴，此事相机永远是面对P1，于是相机可能的位置就是在以P1为球心的球面上，再一个就是球的半径也无法确定，于是有无数个解。

Case2：当N=2时

现在多了一个约束条件，显然OcP1P2形成一个三角形，由于P1、P2两点位置确定，三角形的变P1P2确定，再加上向量OcP1，OcP2从Oc点射线特征点的方向角也能确定，于是能够计算出OcP1的长度=r1，OcP2的长度=r2。于是这种情况下得到两个球：以P1为球心，半径为r1的球A；以P2为球心，半径为r2的球B。显然，相机位于球A，球B的相交处，依旧是无数个解。

Case3：当N=3时

与上述相似，这次又多了一个以P3为球心的球C，相机这次位于ABC三个球面的相交处，终于不再是无数个解了，这次应该会有4个解，其中一个就是我们需要的真解了。

Case4：当N大于3时

N=3时求出4组解，好像再加一个点就能解决这个问题了，事实上也几乎如此。说几乎是因为还有其他一些特殊情况，这些特殊情况就不再讨论了。N>3后，能够求出正解了，但为了一个正解就又要多加一个球D显然不够"环保"，为了更快更节省计算机资源地解决问题，先用3个点计算出4组解获得四个旋转矩阵、平移矩阵。根据公式：

将第四个点的世界坐标代入公式，获得其在图像中的四个投影（一个解对应一个投影），取出其中投影误差最小的那个解，就是我们所需要的正解。

 

 

PNP问题的求解原理大致就是上面这样了，至于具体的数学方法还是请大家自己去查阅文献吧，本博客对这个问题的分析就到此为止了。接下来请看通过解PNP问题，求解相机位姿的应用。

2 根据四个特征点估计相机姿态

相机位姿估计1：根据四个特征点估计相机姿态

关键词：位姿估计  OpenCV::solvePnP

用途：各种位姿估计

文章类型：原理、流程、Demo示例

@Author：VShawn([email protected])

@Date:2016-11-18

@Lab: CvLab202@CSU

 

 

前言

本文通过迭代法解PNP问题，得到相机坐标系关于世界坐标系的旋转矩阵R与平移矩阵T后，根据之前的文章《根据相机旋转矩阵求解三个轴的旋转角》获得相机坐标系的三轴旋转角，实现了对相机位姿的估计。知道相机在哪后，我们就可以通过两张照片，计算出照片中某个点的高度，实现对环境的测量。

先看演示视频：

原理简介

相机位姿估计就是通过几个已知坐标的特征点，以及他们在相机照片中的成像，求解出相机位于坐标系内的坐标与旋转角度，其核心问题就在于对PNP问题的求解，这部分本文不再啰嗦，参见本人之前的博客文章《相机位姿估计0：基本原理之如何解PNP问题》。本文中对pnp问题的求解直接调用了OpenCV的库函数"solvePnP"，其函数原型为：

bool solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=ITERATIVE )

第一个输入objectPoints为特征点的世界坐标，坐标值需为float型，不能为double型，可以输入mat类型，也可以直接输入vector 。

第二个输入imagePoints为特征点在图像中的坐标，需要与前面的输入一一对应。同样可以输入mat类型，也可以直接输入vector 。

第三个输入cameraMatrix为相机内参数矩阵，大小为3×3，形式为：

第四个输入distCoeffs输入为相机的畸变参数，为1×5的矩阵。

第五个rvec为输出矩阵，输出解得的旋转向量。

第六个tvec为输出平移向量。

第七个设置为true后似乎会对输出进行优化。

最后的输入参数有三个可选项：

CV_ITERATIVE，默认值，它通过迭代求出重投影误差最小的解作为问题的最优解。

CV_P3P则是使用非常经典的Gao的P3P问题求解算法。

CV_EPNP使用文章《EPnP: Efficient Perspective-n-Point Camera Pose Estimation》中的方法求解。

流程

1.从函数的原型看出函数需要相机的内参数与畸变参数，于是相机标定是必不可少的，通过OpenCV自带例程或者Matlab的相机标定工具箱都可以很方便地求出相机标定参数。

2.准备好四个特征点的世界坐标，存入Mat矩阵

vector Points3D;
Points3D.push_back(cv::Point3f(0, 0, 0));         //P1 三维坐标的单位是毫米
Points3D.push_back(cv::Point3f(0, 200, 0));       //P2
Points3D.push_back(cv::Point3f(150, 0, 0));       //P3
Points3D.push_back(cv::Point3f(150, 200, 0));     //P4

3.准备好四个特征点在图像上的对应点坐标，这个坐标在实验中我是通过PhotoShop数出来的。注意，输入坐标的顺序一定要与之前输入世界坐标的顺序一致，就是说点与点要对应上，OpenCV的函数无法解决点与点匹配的问题（对应搜索问题）。

vector Points2D;
Points2D.push_back(cv::Point2f(3062, 3073));         //P1 单位是像素
Points2D.push_back(cv::Point2f(3809, 3089));         //P2
Points2D.push_back(cv::Point2f(3035, 3208));         //P3
Points2D.push_back(cv::Point2f(3838, 3217));         //P4

4.创建输出变量，即旋转矩阵跟平移矩阵的变量。最后调用函数。

//初始化输出矩阵
cv::Mat rvec = cv::Mat::zeros(3, 1, CV_64FC1);
cv::Mat tvec = cv::Mat::zeros(3, 1, CV_64FC1);

 //三种方法求解
solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec,  false , CV_ITERATIVE);     //实测迭代法似乎只能用共面特征点求位置
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_P3P);        //Gao的方法可以使用任意四个特征点
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_EPNP);

5将输出的旋转向量转变为旋转矩阵

//旋转向量变旋转矩阵
double  rm[9];
cv::Mat rotM(3, 3, CV_64FC1, rm);
Rodrigues(rvec, rotM);

6.最后根据《根据相机旋转矩阵求解三个轴的旋转角》一文求出相机的三个旋转角，根据《子坐标系C在父坐标系W中的旋转》求出相机在世界坐标系中的位置。

至此，我们就求出了相机的位姿。

实验

本人在实验中先后使用了两台相机做测试，一台是畸变较小的sony a6000微单+35mm定焦镜头，另一台是畸变较重的130w的工业相机+6mm定焦广角镜头，实验中两台相机都得到了正确的位姿结果，此处为了方便只用α6000微单做演示说明。

如上图所示，四个特征点P1-P4的世界坐标与像素坐标都已在图中标明，P5用于重投影验证位姿解是否正确。

相机实际位姿大约为：

 

粗略读出卷尺读数，得到相机的世界坐标大约为(520,0,330)。细心的读者应该发现了，上面几张图的特征点不一样了，其实是我中途重新做了一张特征点图，重新安放实验装置的时候已经尽量按照(520,0,330)这个坐标去安放了，但误差肯定是不可避免的。

 

把参数输入例程中，得到结果，计算出相机的世界坐标：

也就是(528.6,-2.89,358.6)，跟实际情况还是差不多的。

同时还得到了x y z轴的三个旋转角

自己动手转一转相机，发现也是对的。

对P5点重投影，投影公式为：

结果为：

误差在10pix以内，结果也是正确的，于是验证完毕。

 

P.S.经本人测试发现，solvePnP提供的三种算法都能对相机位姿进行估计，虽然三者直接解出的结果略有不同，但都在误差范围之内。其中solvePnP的默认方法迭代法，似乎只能使用共面的四个特征点求位姿，一旦有一个点不共面，解出的结果就会不对。

例程

最后给出例程，例程基于VS2013开发，使用的是OpenCV2.4.X，大家运行前需要将opencv的路径重新配置成自己电脑上的，不懂的话参考我的博客《OpenCV2+入门系列（一）：OpenCV2.4.9的安装与测试》。例程中提供两张照片，其中DSC03323就是"实验"中所用图片，例程在计算完成后，会在D盘根目录下生成两个txt，分别存储：相机在世界坐标系的坐标、相机的三个旋转角。

 

下载地址：

CSDN：http://download.csdn.net/detail/wx2650/9688155

GIT：https://github.com/vshawn/Shawn_pose_estimation_by_opencv

3 OpenCV:solvePnP二次封装与性能测试

转自  http://www.cnblogs.com/singlex/p/pose_estimation_1_1.html

相机位姿估计1_1：OpenCV:solvePnP二次封装与性能测试

关键词：OpenCV::solvePnP

文章类型：方法封装、测试

@Author：VShawn([email protected])

@Date:2016-11-27

@Lab: CvLab202@CSU

前言

今天给大家带来的是一篇关于程序功能、性能测试的文章，读过《相机位姿估计1：根据四个特征点估计相机姿态》一文的同学应该会发现，直接使用OpenCV的solvePnP来估计相机位姿，在程序调用上相当麻烦，从一开始的参数设定到最后将计算出的矩阵转化为相机的位姿参数，需要花费近两百行代码。因此为了更方便地调用程序，今天我就给大家带来一个我自己对solvePnP的封装类PNPSolver，顺便将OpenCV自带的三种求解方法测试一遍。

类的封装

封装的思路我就不写了，由于博客更新速度赶不上我写程序的速度，现在发上来的类已经修改过好几次了，思路也换了几次。不过大的方向没变，目的就是只需要输入参数，输入坐标点后直接可以得到相机在世界坐标系的坐标。

类的调用顺序：

1.初始化PNPSolver类；

2.调用SetCameraMatrix(),SetDistortionCoefficients()设置好相机内参数与镜头畸变参数；

3.向Points3D，Points2D中添加一一对应的特征点对；

4.调用Solve()方法运行计算；

5.从属性Theta_C2W中提取旋转角，从Position_OcInW中提取出相机在世界坐标系下的坐标。

以下是类体：

PNPSolver.h

+ View Code

PNPSolver.cpp

+ View Code

　　

一个典型的调用示例

//初始化PNPSolver类
PNPSolver p4psolver;
//初始化相机参数
p4psolver.SetCameraMatrix(fx, fy, u0, v0);
//设置畸变参数
p4psolver.SetDistortionCoefficients(k1, k2, p1, p2, k3);
 //设置特征点的世界坐标
p4psolver.Points3D.push_back(cv::Point3f(0, 0, 0));      //P1三维坐标的单位是毫米
p4psolver.Points3D.push_back(cv::Point3f(0, 200, 0));    //P2
p4psolver.Points3D.push_back(cv::Point3f(150, 0, 0));    //P3
//p4psolver.Points3D.push_back(cv::Point3f(150, 200, 0));   //P4
p4psolver.Points3D.push_back(cv::Point3f(0, 100, 105));  //P5

cout <<  "test2:特征点世界坐标 = "  << endl << p4psolver.Points3D << endl;
 //设置特征点的图像坐标
p4psolver.Points2D.push_back(cv::Point2f(2985, 1688));   //P1
p4psolver.Points2D.push_back(cv::Point2f(5081, 1690));   //P2
p4psolver.Points2D.push_back(cv::Point2f(2997, 2797));   //P3
//p4psolver.Points2D.push_back(cv::Point2f(5544, 2757));    //P4
p4psolver.Points2D.push_back(cv::Point2f(4148, 673));    //P5

cout <<  "test2:图中特征点坐标 = "  << endl << p4psolver.Points2D << endl;

if  (p4psolver.Solve(PNPSolver::METHOD::CV_P3P) == 0)
    cout <<  "test2:CV_P3P方法:  相机位姿→"  <<  "Oc坐标="  << p4psolver.Position_OcInW <<  "    相机旋转="  << p4psolver.Theta_W2C << endl;
if  (p4psolver.Solve(PNPSolver::METHOD::CV_ITERATIVE) == 0)
    cout <<  "test2:CV_ITERATIVE方法:    相机位姿→"  <<  "Oc坐标="  << p4psolver.Position_OcInW <<  "    相机旋转="  << p4psolver.Theta_W2C << endl;
if  (p4psolver.Solve(PNPSolver::METHOD::CV_EPNP) == 0)
    cout <<  "test2:CV_EPNP方法: 相机位姿→"  <<  "Oc坐标="  << p4psolver.Position_OcInW <<  "    相机旋转="  << p4psolver.Theta_W2C << endl;

方法测试

OpenCV提供了三种方法进行PNP计算，三种方法具体怎么计算的就请各位自己查询opencv documentation以及相关的论文了，我看了个大概然后结合自己实际的测试情况给出一个结论，不一定正确，仅供参考：

方法名	说明	测试结论
CV_P3P	这个方法使用非常经典的Gao方法解P3P问题，求出4组可能的解，再通过对第四个点的重投影，返回重投影误差最小的点。 论文《Complete Solution Classification for the Perspective-Three-Point Problem》	可以使用任意4个特征点求解，不要共面，特征点数量不为4时报错
CV_ITERATIVE	该方法基于Levenberg-Marquardt optimization迭代求解PNP问题，实质是迭代求出重投影误差最小的解，这个解显然不一定是正解。 实测该方法只有用4个共面的特征点时才能求出正确的解，使用5个特征点或4点非共面的特征点都得不到正确的位姿。	只能用4个共面的特征点来解位姿
CV_EPNP	该方法使用EfficientPNP方法求解问题，具体怎么做的当时网速不好我没下载到论文，后面又懒得去看了。 论文《EPnP: Efficient Perspective-n-Point Camera Pose Estimation》	对于N个特征点，只要N>3就能够求出正解。

测试截图：

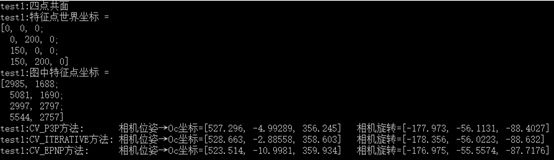
1.使用四个共面的特征点，显然三种方法都能得到正解，但相互之间略有误差。

2使用四个非共面的特征点，CV_ITERATIVE方法解错了。

3.使用5个特征点求解，只有CV_EPNP能够用

性能测试

最后对三种方法的性能进行测试，通过对test1重复执行1000次获得算法的运行时间，从结果可以看出迭代法显然是最慢的，Gao的P3P+重投影法用时最少，EPNP法其次。

总结

综合以上的测试，推荐使用CV_P3P来解决实际问题，该方法对于有四个特征点的情况限制少、运算速度快。当特征点数大于4时，可以取多组4特征点计算出结果再求平均值，或者为了简单点就直接使用CV_EPNP法。

不推荐使用CV_ITERATIVE方法。

 

 4  实时位姿估计与三维重建相机姿态

前言

本文将展示一个实时相机位姿估计的例程，其中的原理在前文中已经说过了，再利用《相机位姿估计1_1：OpenCV、solvePnP二次封装与性能测试》中构建的类，使得程序处理更加简单。本例程利用HSV空间，跟踪红色的特征点，将跟踪到的特征点用于解PNP问题，得到相机位姿（相机的世界坐标与相机的三个旋转角）。最后使用labview中的三维图片控件，对整个系统进行3D重建。

处理流程

1. 首先初始化工业相机，采集到实时图像，使用imshow显示图片。
2. 在实时的相机采图中，依次选取P1、P2、P3、P4（在前文《相机位姿估计1：根据共面四点估计相机姿态》中有提及），一定要按顺序点，否则无法获得正确位姿。选取完成后立即对该点进行追踪。
3. 当跟踪的特征点数量达到4个时，程序开始调用PNPSolver类估计相机位姿。
4. 将得到的位姿信息写入txt，位于D盘根目录（这就是上一篇文章中为什么要写文件的原因）。
5. Labview程序运行后不断读取txt，将读到的位姿数据应用到3D中，绘制出正确的三维场景。（这里两个进程通过txt通讯效率很低，但我偷懒了，没有再去编写更好的程序）

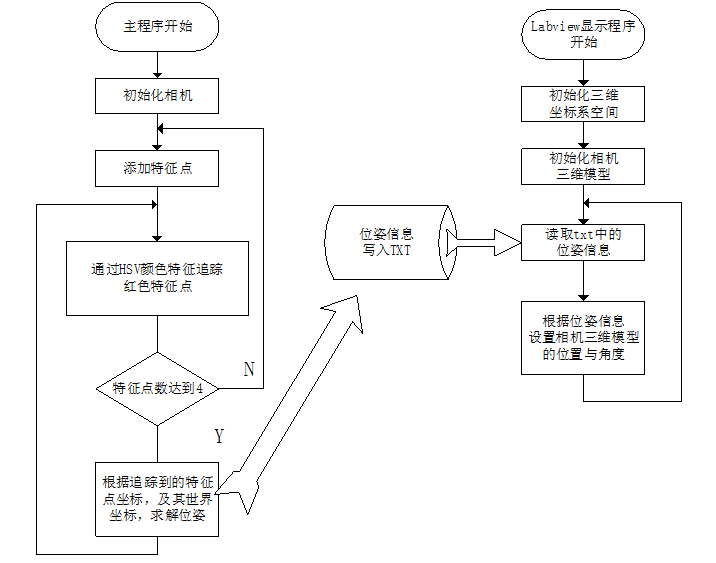
用流程图来表示就是：

过程非常简单，C++程序用来计算位姿，labview程序用于显示。

（对于不懂labview的读者：也可以通过OpenGL来实现显示部分）

特征点跟踪方法

为了偷懒省事，这里的特征点跟踪直接使用了最简单的跟踪颜色的方法。我做的标志图是这样的：

每个特征点都是红色马克笔涂出的红点。

在实际操作中用户首先在显示界面中按照顺序（程序中点的世界坐标输入顺序）点击特征点，得到特征点的初始位置。根据初始位置，在其附近选取ROI，将BGR图像转为HSV图像进行颜色分割，针对其H通道进行二值化，将红色区域置为255，得到二值图像。在二值图像中查找连通域，并计算出连通域的重心G的位置，将G的坐标作为本次跟踪结果返回，并作为下一次跟踪的起点。

效果如下图，图中绿色的圈是以重心G为圆心绘制的。

函数如下：

+ View Code

位姿估计

当用户点击了四个特征点后，程序开始运行位姿估计部分。位姿具体的过程不再叙述，请参考前面的博文：

《相机位姿估计1：根据四个特征点估计相机姿态》

《相机位姿估计1_1：OpenCV:solvePnP二次封装与性能测试》

三维显示

位姿估计完成后，会输出两个txt用于记录相机当前的位姿。

Labview程序就是读取这两个txt的信息，进而显示出三维空间。labview程序的编程过程比较难叙述，思路便是首先建立世界坐标系，然后在世界坐标系中创建一个三维物体作为相机的三维模型。然后根据txt中的信息，设置这个模型所在的位置（也就是三维坐标），再设置该模型的三个自旋角，完成三维绘制。

上述流程可以运行项目文件夹中的：

~\用LabView重建相机位置\世界-手动调整参数设置相机位姿.vi

来手动设置参数，体验绘图的流程。

 

对该部分感兴趣的人可以参考文档：

http://zone.ni.com/reference/zhs-XX/help/371361J-0118/lvhowto/create_3d_scene/

效果演示

这演示以前也有放出来过，就是实时跟踪特征点，再在右边重建相机姿态。

 

程序下载

最后给出例程，例程C++部分基于VS2013开发，使用的是OpenCV2.4.X，三维重建部分使用Labview2012开发。OpenCV配置参考我的博客《OpenCV2+入门系列（一）：OpenCV2.4.9的安装与测试》，Labview则是直接安装好就行。

例程下载后，需要将图像采集部分修改为你的相机驱动，然后修改相机参数、畸变参数就能够使用了。

地址：

C++程序：Github

LabView程序：Github

程序下载地址：Github

作者：VShawn

出处：http://www.cnblogs.com/singlex/

本文版权归作者所有，欢迎转载，但未经博客作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。