算法排序（快速排序/冒泡排序/直接插入排序/堆排序等）汇总，原理，图解及代码案例

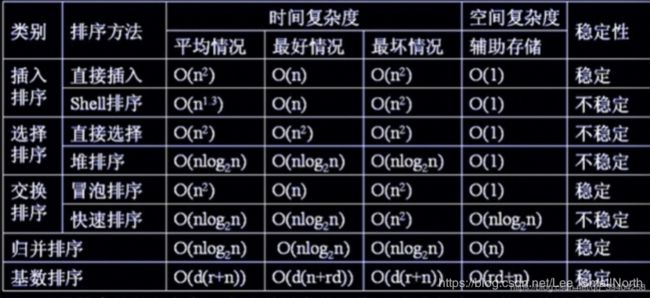
常用排序的时间及空间复杂度

一、快速排序
原理：
快速排序使用分治法策略把一个序列分成两个子序列，再简单来说，就是分成左右两个区，选择一个基数（固定数或者根据索引选择第一个），把大于这个基数的放在右边，小于放在左边，这里有个知识点要注意：
图片来源网络：

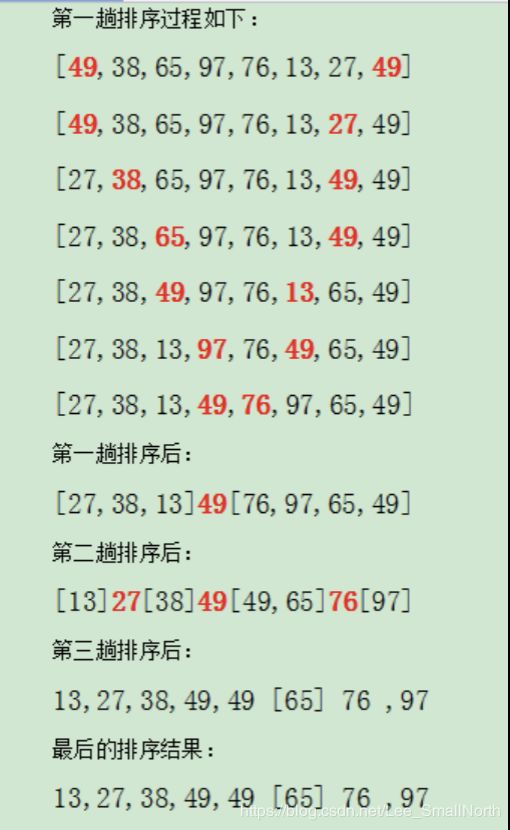
举个
{31,78,29,10,96,65,12,46}
把数组第一个当作基数，从右开始执行一趟排序得到
{12 10 29 31 96 65 78 46}
1.如果当前被选中的值小于基数
从左向右填充
2.如果当前被选中的值等于基数
不移动
3.如果当前被选中的值大于基数
从最右往左填充
一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；

4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；

5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）
代码案例：

package com.portal;

import java.util.Arrays;

/**
 * 快速排序算法
 * @author xiaobei
 *
 */
public class QuickSort {
	/**
	 * 
	 * @param arr 要排序的数组
	 * @param low 区间开始地址 也就是索引
	 * @param high 区间结束地址
	 */
	public static void quickSort(int[] arr,int low,int high	) {
		int l = low; //区间开始地址
		int h = high;//区间结束地址
		
		if (l > h) {//防止索引越界
			return;
		}
		int temp = arr[low]; //数组的第一个值作为基数
		//1.创建l=0;h=5;temp=6
		//2.l=0;h=3;temp=6
		while (l < h) {
			//从右开始找出最小的数
			while (l < h && arr[h] > temp) {
				h--;
			}
			//从左开始找出最大的数
			while (l

 

二、冒泡排序
原理：
每次比较两个相邻的元素，将较大的元素交换至右侧。

基本思想：每次冒泡排序都会将两个相邻的元素进行比较，看是否满足大小要求，如果不满足，就交换这两个相邻元素的次序，一次冒泡至少让一个元素移动到它应该排列的位置，重复N次，就完成了冒泡排序。

图片来源网络：【注意：图中每一竖列是一次比较交换】

代码案例：

public static void main(String[] args) {
		int[] arr = {8,12,4,23,6,7,25,10,2};
		for (int i = 1; i < arr.length; i++) {
			for (int j = 0; j < arr.length - i; j++) {
				if (arr[j] < arr[j + 1]) {
					int temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
			}
		}
		System.out.println("************排序后：****************");
		System.out.print("\t"+Arrays.toString(arr));
	}

 三、直接插入排序

原理：每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表依然有序。

算法描述：

对一个有n个元素的数据序列，排序需要进行n-1趟插入操作：

第1趟插入，将第2个元素插入前面的有序子序列--此时前面只有一个元素，当然是有序的。

第2趟插入，将第3个元素插入前面的有序子序列，前面2个元素是有序的。

第n-1趟插入，将第n个元素插入前面的有序子序列，前面n-1个元素是有序的。

图片来源于网络：

代码案例：

public static void main(String[] args) {
		int[] data = {13,7,4,23,8,7,3,9,10,21};
		System.out.print("\r\n排序前：");
		System.out.print("\t" + Arrays.toString(data));
		for (int i = 1; i < data.length; i++) {
			int temp  = data[i];
			if (data[i] < data[i-1]) {
				int j = i-1;
				while (j >= 0 && data[j] > temp) {
					data[j + 1] = data[j];
					j--;
				}
				data[j + 1] = temp;
			}
		}
		System.out.print("\r\n排序后：");
		System.out.print("\t" + Arrays.toString(data));
	}

四、堆排序

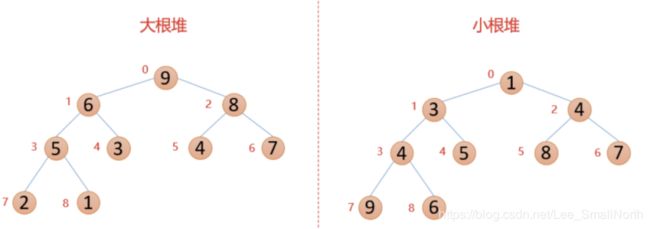
什么是堆

堆通常是一个可以被看做一棵树的数组对象。

堆的时间复杂度O(N*logN),额外空间复杂度O(1),是一个不稳定的排序

堆的数据结构

大根堆：每个结点的值都大于其左孩子和右孩子结点的值

小根堆：每个结点的值都小于其左孩子和右孩子结点的值

如图：

 

上图结构映射成数组

 

完全二叉树有个特性

左边子节点位置=当前父节点的2倍+1

右边子节点位置=当前父节点的2倍+2

父：A编号

左：2A + 1

右：2A + 2

知识点：一般升序采用大顶堆，降序采用小顶堆。

代码案例：逻辑有点难理解，可以多写几遍并且跟着代码看

package com.portal;

import java.util.Arrays;

/**
 * 堆排序
 * @author xiaobei
 *
 */
public class HeapSort {
	
	public static void main(String[] args) {
		int[] arr = {5,1,9,10,4,6,18,21,3,7};
		sort(arr);
		System.out.println(Arrays.toString(arr));
	}
	public static void sort(int[] arr) {
		//1.构建大顶堆
		for (int i = arr.length/2-1; i >= 0; i--) {
			//1.1从第一个非叶子结点从下至上，从右至左调整结构
			addHeap(arr,i,arr.length);
		}
		//2.调整堆结构+交换堆顶元素和末尾元素
		for (int j = arr.length - 1; j > 0; j--) {
			swap(arr,0,j);//交换堆顶元素和末尾元素
			addHeap(arr, 0, j);//重新对堆进行调整
		}
		
	}
	public static void swap(int[] arr, int i, int j) {
		int temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
		
	}
	public static void addHeap(int[] arr, int i, int length) {
		int temp = arr[i];
		for (int j = i*2+1; j < length; j=j*2+1) {//从i结点的左子结点开始，也就是2i+1处开始
			if (j+1 temp) {//如果子结点大于父结点，将子结点值赋给父节点，不用交换
				arr[i] = arr[j];
				i=j;
			}else {
				break;
			}
		}
		arr[i] = temp;//将temp值放到最终的位置
		
	}
	

}