图的最短路径
从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径叫做最短路径
图的最短路径有许多重要的应用。
例如:上图中v0-v8有9个点,可以看做不同的地点,现在要规划出v0到其它某个点地点的最短路线规划
构建最短路径中比较常见的一种算法即为dijstra(迪杰斯特拉)算法
dijstra(迪杰斯特拉)算法
究竟什么是迪杰斯特拉算法?它是如何寻找图中顶点的最短路径呢?
这个算法的本质,是不断刷新起点与其他各个顶点之间的 “距离表”。
让我们来演示一下迪杰斯特拉的详细过程:
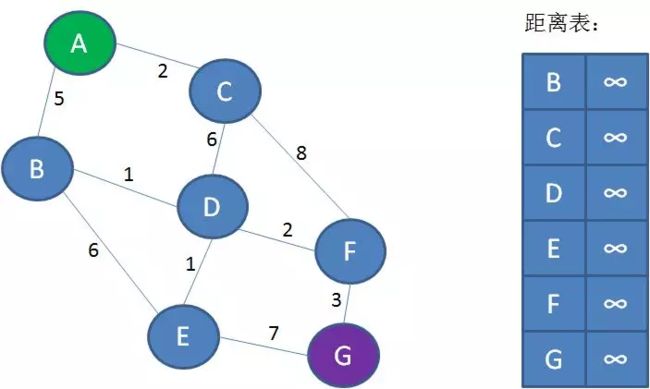
第1步,创建距离表。表中的Key是顶点名称,Value是从起点A到对应顶点的已知最短距离。但是,一开始我们并不知道A到其他顶点的最短距离是多少,Value默认是无限大:
第2步,遍历起点A,找到起点A的邻接顶点B和C。从A到B的距离是5,从A到C的距离是2。把这一信息刷新到距离表当中:
第3步,从距离表中找到从A出发距离最短的点,也就是顶点C。
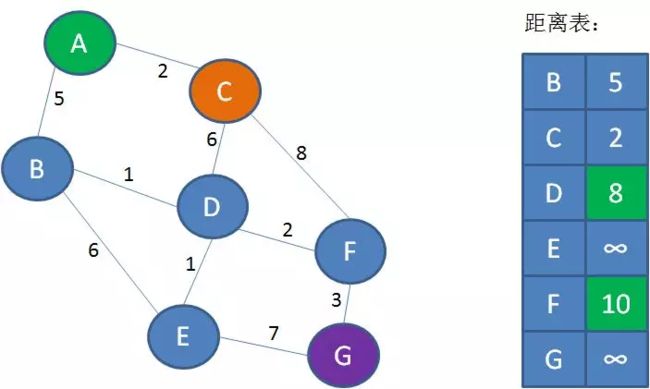
第4步,遍历顶点C,找到顶点C的邻接顶点D和F(A已经遍历过,不需要考虑)。从C到D的距离是6,所以A到D的距离是2+6=8;从C到F的距离是8,所以从A到F的距离是2+8=10。把这一信息刷新到表中:
接下来重复第3步、第4步所做的操作:
第5步,也就是第3步的重复,从距离表中找到从A出发距离最短的点(C已经遍历过,不需要考虑),也就是顶点B。
第6步,也就是第4步的重复,遍历顶点B,找到顶点B的邻接顶点D和E(A已经遍历过,不需要考虑)。从B到D的距离是1,所以A到D的距离是5+1=6,小于距离表中的8;从B到E的距离是6,所以从A到E的距离是5+6=11。把这一信息刷新到表中:
(在第6步,A到D的距离从8刷新到6,可以看出距离表所发挥的作用。距离表通过迭代刷新,用新路径长度取代旧路径长度,最终可以得到从起点到其他顶点的最短距离)
第7步,从距离表中找到从A出发距离最短的点(B和C不用考虑),也就是顶点D。
第8步,遍历顶点D,找到顶点D的邻接顶点E和F。从D到E的距离是1,所以A到E的距离是6+1=7,小于距离表中的11;从D到F的距离是2,所以从A到F的距离是6+2=8,小于距离表中的10。把这一信息刷新到表中:
第9步,从距离表中找到从A出发距离最短的点,也就是顶点E。
第10步,遍历顶点E,找到顶点E的邻接顶点G。从E到G的距离是7,所以A到G的距离是7+7=14。把这一信息刷新到表中:
第11步,从距离表中找到从A出发距离最短的点,也就是顶点F。
第10步,遍历顶点F,找到顶点F的邻接顶点G。从F到G的距离是3,所以A到G的距离是8+3=11,小于距离表中的14。把这一信息刷新到表中:
就这样,除终点以外的全部顶点都已经遍历完毕,距离表中存储的是从起点A到所有顶点的最短距离。显然,从A到G的最短距离是11。(路径:A-B-D-F-G)
代码实现:
/**
* 创建图
*/
public void createGraph(){
int [] a1 = new int[]{0,1,5,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT};
int [] a2 = new int[]{1,0,3,7,5,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT};
int [] a3 = new int[]{5,3,0,MAX_WEIGHT,1,7,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT};
int [] a4 = new int[]{MAX_WEIGHT,7,MAX_WEIGHT,0,2,MAX_WEIGHT,3,MAX_WEIGHT,MAX_WEIGHT};
int [] a5 = new int[]{MAX_WEIGHT,5,1,2,0,3,6,9,MAX_WEIGHT};
int [] a6 = new int[]{MAX_WEIGHT,MAX_WEIGHT,7,MAX_WEIGHT,3,0,MAX_WEIGHT,5,MAX_WEIGHT};
int [] a7 = new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,3,6,MAX_WEIGHT,0,2,7};
int [] a8 = new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,9,5,2,0,4};
int [] a9 = new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,7,4,0};
matrix[0] = a1;
matrix[1] = a2;
matrix[2] = a3;
matrix[3] = a4;
matrix[4] = a5;
matrix[5] = a6;
matrix[6] = a7;
matrix[7] = a8;
matrix[8] = a9;
}
package cn.itcast.grape;
import cn.itcast.treeandgrape.Graph;
public class JavaDijstra {
private final static int MAXVEX = 9;//顶点,以后不需要写死
private final static int MAXWEING = 65535;//(最大)权重
private int shortTablePath[] = new int[MAXVEX];//存储V0到某顶点最短路径的权值和 例:{0,1,5}
/**
* 获取一个图的最短路径
*/
public void shortestPathDijstra(Graph graph) {
int min;//最小值
int k = 0;//记录下标
boolean isgetPath[] = new boolean[MAXVEX];//是否已经拿到了V0到Vm的最短路径
for (int v = 0; v < graph.getVertexSize(); v++) {//遍历顶点数量
shortTablePath[v] = graph.getMatrix()[0][v];//获得V0这一行的权值数组
}
shortTablePath[0] = 0;//V0到V0的距离是0, 拿到数据后,不必往回走
isgetPath[0] = true;
for (int v = 1; v < graph.getVertexSize(); v++) {//横向
min = MAXWEING;//初始化
for (int w = 0; w < graph.getVertexSize(); w++) {//纵向,对找出来的顶点一个一个遍历
if (!isgetPath[w] && shortTablePath[w] < min) {
k = w;
min = shortTablePath[w];
}
}
isgetPath[k] = true;
for (int j = 0; j < graph.getVertexSize(); j++) {
if (!isgetPath[j] && (min + graph.getMatrix()[k][j] < shortTablePath[j])) {
shortTablePath[j] = min + graph.getMatrix()[k][j];
}
}
}
for (int i = 0; i < shortTablePath.length; i++) {
System.out.println("V0到V" + i + "的最短路径为:" + shortTablePath[i] + "\n");
}
}
public static void main(String[] args) {
Graph graph = new Graph(MAXVEX);
graph.createGraph();
JavaDijstra dijstra = new JavaDijstra();
dijstra.shortestPathDijstra(graph);
}
}
图的拓扑排序
相关概念
AOV网:在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,称为AOV网(Activity On Vertex)。
AVO网不存在环路
拓扑序列:设G=(V,E)是一个具有n个顶点的有向图,V中顶点序列V1,V2,......,Vn,满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前,则这样的顶点序列称为一个拓扑序列。
拓扑序列并不唯一
拓扑排序就是构造拓扑序列的过程,当AOV网中不存在环路时,全部顶点都会被输出。
拓扑排序算法
思想:从AOV网中选择一个入度为0的顶点输出,然后删除此顶点,并删除一次顶点为尾的弧,继续重复该步骤,直至输出全部顶点或者AOV网中不存在入度为0的顶点为止。
由于拓扑排序需要删除顶点,所以使用邻接表的方式存储图会较为方便
邻接表结构
邻接表的结构不局限于此,可以根据实际情况添加字段,如在拓扑排序中可以在顶点表中增加入度字段,用于统计每个顶点的入度情况。在带权图中可以在边表中添加weight字段,用于表示每条边的权值。
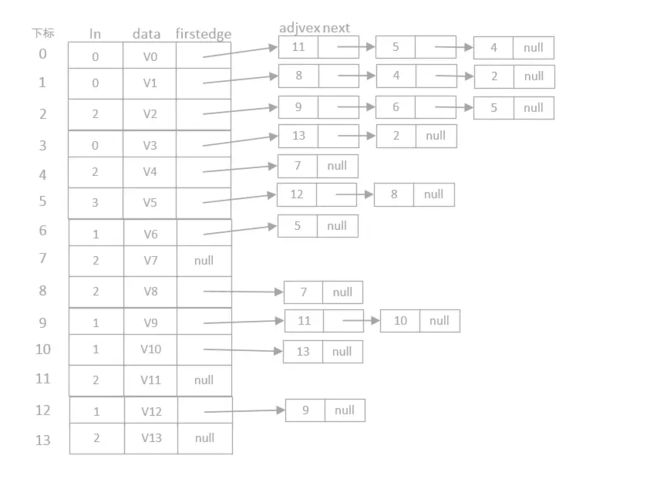
测试图:
对应的邻接表结构:
代码实现:
package cn.itcast.grape; import java.util.Stack; public class DnGraphTopologic { private int numVertexes; private VertexNode[] adjList;//邻接顶点的一维数组 public DnGraphTopologic(int numVertexes) { this.numVertexes = numVertexes; } private void createGraph() { VertexNode node0 = new VertexNode(0, "v0"); VertexNode node1 = new VertexNode(0, "v1"); VertexNode node2 = new VertexNode(2, "v2"); VertexNode node3 = new VertexNode(0, "v3"); VertexNode node4 = new VertexNode(2, "v4"); VertexNode node5 = new VertexNode(3, "v5"); VertexNode node6 = new VertexNode(1, "v6"); VertexNode node7 = new VertexNode(2, "v7"); VertexNode node8 = new VertexNode(2, "v8"); VertexNode node9 = new VertexNode(1, "v9"); VertexNode node10 = new VertexNode(1, "v10"); VertexNode node11 = new VertexNode(2, "v11"); VertexNode node12 = new VertexNode(1, "v12"); VertexNode node13 = new VertexNode(2, "v13"); adjList = new VertexNode[numVertexes]; adjList[0] = node0; adjList[1] = node1; adjList[2] = node2; adjList[3] = node3; adjList[4] = node4; adjList[5] = node5; adjList[6] = node6; adjList[7] = node7; adjList[8] = node8; adjList[9] = node9; adjList[10] = node10; adjList[11] = node11; adjList[12] = node12; adjList[13] = node13; node0.firstEdge = new EdgeNode(11); node0.firstEdge.next = new EdgeNode(5); node0.firstEdge.next.next = new EdgeNode(4); node1.firstEdge = new EdgeNode(8); node1.firstEdge.next = new EdgeNode(4); node1.firstEdge.next.next = new EdgeNode(2); node2.firstEdge = new EdgeNode(9); node2.firstEdge.next = new EdgeNode(6); node2.firstEdge.next.next = new EdgeNode(5); node3.firstEdge = new EdgeNode(13); node3.firstEdge.next = new EdgeNode(2); node4.firstEdge = new EdgeNode(7); node5.firstEdge = new EdgeNode(12); node5.firstEdge.next = new EdgeNode(8); node6.firstEdge = new EdgeNode(5); node8.firstEdge = new EdgeNode(7); node9.firstEdge = new EdgeNode(11); node9.firstEdge.next = new EdgeNode(10); node10.firstEdge = new EdgeNode(13); node12.firstEdge = new EdgeNode(9); } /** * 拓扑排序 */ private void topologicalSort() throws Exception { Stackstack = new Stack<>(); int count = 0;//计数,看拓扑排序是不是正确 int k = 0; for (int i = 0; i < numVertexes; i++) { if (adjList[i].in == 0) { stack.push(i); } } while (!stack.isEmpty()) { int pop = stack.pop();//弹出栈 System.out.println("顶点:" + adjList[pop].data); count++; for (EdgeNode node = adjList[pop].firstEdge; node != null; node = node.next) {//横向遍历 k = node.adjVert;//下标 if (--adjList[k].in == 0) { stack.push(k);//入度为0,入栈 } } } if (count<numVertexes){ throw new Exception("拓扑排序失败"); } } //边表顶点(横) class EdgeNode { private int adjVert;//下标 private EdgeNode next; private int weight;//全重,先看有没有权重 public EdgeNode(int adjVert) { this.adjVert = adjVert; } public int getAdjVert() { return adjVert; } public void setAdjVert(int adjVert) { this.adjVert = adjVert; } public EdgeNode getNext() { return next; } public void setNext(EdgeNode next) { this.next = next; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } } //邻接顶点(纵) class VertexNode { private int in;//入度 private String data; private EdgeNode firstEdge; public VertexNode(int in, String data) { this.in = in; this.data = data; } } public static void main(String[] args) { DnGraphTopologic dnGraphTopologic = new DnGraphTopologic(14); dnGraphTopologic.createGraph(); try { dnGraphTopologic.topologicalSort(); } catch (Exception e) { e.printStackTrace(); } } }