学习进制及数据在计算机中的表示

进制------即进位计数制

★数的编码表示:在计算机中,因为只有0和1两种形式,因此数的正、负也要进行0和1编码. 通常把一个数的最高位定义为符号位,用0表示正 , 用1 表示负,最高位称为数符位,其余位仍表示数值.

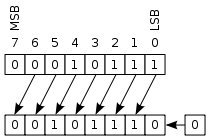
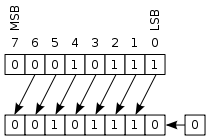
★一个8位的二进制数  -0101100,它在计算机中可表示为10101100,如图所示:

1

0

1

0

1

1

0

0

数符位(1位)  数值位(7位)

★规则:将一个数在计算机中的表示形式称为" 机器数 ",而它代表的数值称为此机器数的"真值". 在上例中,10101100称为"机器数",而 -0101100称为此机器数的"真值";

(要习惯于这种二进制数"真值"的写法,就如同一个十进制 -10 一样去认识.)

★那么通过上述的规则,将数的符号数字化(0/1)后,计算机就可以识别和表示数符了.但问题又出现了:如果数符位和数值位同时参加运算,有时会产生错误的结果;若要让计算机另外考虑符号的问题,将增加计算机实现的难度( 因为计算机非常笨<_> ).那么如何让傻傻的计算机能够将符号位与数值位同等对待,并且计算结果不错呢? 

★为了解决此类问题:在机器数中常采用多种编码方式表示符号数,常用的是原码,反码及补码(in two's complement).这些编码的实质是对负数用机器数表示的不同的编码

★原则: 整数X的补码:对于正数,补码与原码,反码相同 , 对于负数,数符位为1,其

数值位X的绝对值取反后最低位+1,即为反码+1.

对于0,[+0]补=0000 0000,[-0]补=0000 0000.

 

重点掌握:1.多项式(权值)概念

2.进制间相互转换

1.其实很简单:可以类比更常见的十进制来理解其他各个进制.(每一个进制数值都可以写成一个多项式,每个项是每个位置的数码与此位置对应的权值相乘)

在采用进位计数的数字系统中,如果只用 r 个基本符号(例如:0,1)表示数值,则称其为 r 进制数. r 称为该数制的基数(Radix),而数制中每一个固定位置的单位值称为 权.

不同的数制有两个共同的特点:1.是采用进位计数制的方式,每一种数制都有固定的基本符号,称为数码.2.是都使用位置表示法,即处于不同位置的数码所代表的值不同,与它所在位置的权值有关.

2.十进制数转换成r进制数

先将此数分成整数与小数两部分分别转换,然后同去拼接起来即可.

整数部分采用除r取余法:将十进制数不断除以r取余数 ,直到商为0,余数从右至左排列,首次取得的余数在最右边,即低位.

小数部分采用乘r取整法:将小数不断乘以r取整数,直到小数为0或者达到所需要精度(小数可能永远不为0),所得整数则从左至右排列,先取到的整数在左边,即高位.

3.引入8进制与16进制

原因:为了方便,可以借助于8进制与16进制来进行转换或表示.

特殊关系:1位8进制数相当于3位2进制数,1 位十六进制数相当于4位二进制数.因此转换非常方便.

转换规则:以小数点为中心向左右两边分两组,每3(4)位为一组,两头不足补0即可.

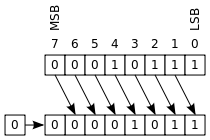
★为什么JAVA中将一个byte(8位)转化成32位的INT,然后再MASK with 0XFF后,再转化成十六进制?

★★★★★   Stackoverflow上一个详细的回答(了解JAVA中的机器数,进制数间的相互转换原理),地址如下:

We want to convert a byte value (or an array of bytes) to a string which represents a hexadecimal value in ASCII.

★Arithmetic Shift(算术移位):( ">>" & "<<" ) In an arithmetic shift,the bits that are shifted out of either end are discarded. In a left arithmetic shift,zeros are shifted in on the right ;In a right arithmetic shift,the sign bit is shifted in on the left, thus preserving the sign of the operand.

★Logical Shift(逻辑移位): (only ">>>") In a logical shift,zeros are shifted in to replace the discarded bits,to both

left shift and right shift. Therefore, the logical and arithmetic left-shifts are exactly the same.

However, as the logical right-shift inserts value 0 bits into the most significant bit,instead of

copying the sign bit, it is ideal for unsigned binary numbers, while the arithmetic right-shift is

ideal for signed two's complements binary numbers.

★Shifts in java: In java,all integer types(所有的整数类型)are signed , so the "<<" & " >>" operators perform arithmetic shifts.

Java adds the operator ">>>" to perform logical right shifts,but since the logical and arithmetic left-shift

operations are identical for signed integer(整数),there is no "<<<" operator in java.

More details of Java shift operators:

~The operator "<<" (left shift),">>"(signed right shift),and ">>>"(unsigned right shift) are called the shift operators(移位操作符).

~The value of n">>>"s is n right-shifted s bit positions with zero-extension.

~In bit and shift operations,the type byte is implicitly converted to int. If the byte value is negative,the highest bit is

one,then ones are used to fill up the extra bytes in the int .So byte b=-5; int i=b | 0x0200 ; will give i==-5 as result.

★Sign Extension(符号扩展): It's the operation of increasing the number of the bits of a binary number while preserving the number's sign(positive or negative) and

the value .This is done by appending digits to the most significant side of the number , following(在...之后) a procedure dependent on the particular

signed number representation (应该翻译成:有符号数表示方法 , 有原码,反码,补码等4种表示方法,而补码(two's complement)是最最常用的表示负数的方法) used.