机器学习算法(一)线性回归的原理以及代码实现
线性回归(Linear regression)
线性回归作为机器学习中的一个基本算法,他的目的、功能、用途都是相当的明了,在这篇文章中会简单的介绍和说明线性回归的原理,然后使用python实现效果,最后会在其他的文章中补充一些进一步的优化
线性回归的目的 很简单,就是用一条直线来拟合这些点。
线性回归的功能 也很直接,通过大量的训练集进行训练,得到合适的权重参数
θ,随之输入测试集或者验证集的数据,对其进行预测。
线性回归的简单用途 可以用来进行房价收入等的预测,
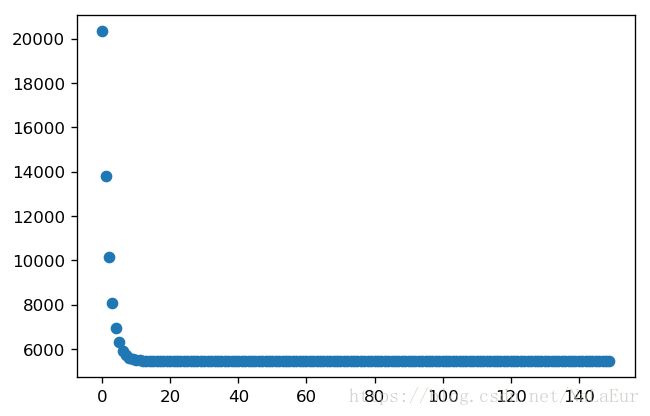
数据来自于GradientDescentExample中的data.csv文件,共100个数据点,如下图所示:

我们的目的就是做出一根直线对数据进行拟合,在开始之前我们先简单的介绍一些相关概念以及推导。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def load_data ():
data = pd.read_csv ('data.csv')
data = np.array (data)
# 手动添加一列
data = np.insert(data, 0, values = 1, axis = 1)
X = data [: ,0:-1]
Y = data [:, -1]
return X, Y
def show_data (X, y):
plt.figure (dpi = 120)
plt.scatter (X[:, -1], y)
plt.show()
if __name__ == '__main__':
X , Y = load_data()
show_data (X, Y)损失函数的推导过程
在线性回归中,我们用x1 ,x2,…, xn 来表示每个数据中的n个feature,用ω来表示每个特征变量x的系数,就像我们平去猜考虑期末考试回家会不会挨骂那样,我们会将许多因素都考虑进去,比如说考试分数,爸爸的心情,有没有拿奖状,以及隔壁家小孩考了多少分等等因素,最后可以得到一个预测公式,也就是拟合函数:
![]() 其中x0=1
其中x0=1
这就是我们的预测函数,当然预测函数和真实值之间是有误差的,我们的目的就是缩小这个误差,那么从上面的公式中可以看到,缩小误差的核心目标那就是缩小参数ω,这个目标也就是线性回归的核心内容,那么下面我们就要先设置出损失函数J(ω)
- 首先我们开始定义变量的符号
1. y 表示为训练集所提供的结果
2. W 表示为预测函数中每个变量权重的向量形式
3. X 表示为训练集中每个变量的向量形式
4. ε 表示为真实值与预测值之间结果的误差
5. m 表示为训练集的数据数目
6. i 表示为这是训练集中的第几个数据
7. j 表示为这是数据中的第j个特征
那么真实值与预测值之间的关系可以用下式进行表示

其中 误差 ε 符合正态分布,就像去食堂打饭一样,喊阿姨少几块肉,喊姐姐多几块肉,永远会在那个区间上下浮动一样,那么ε值的概率公式为
- 由上式可以看出ε与L的关系,随之求最大似然估计
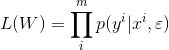
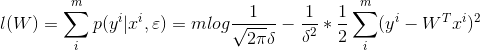
- 那么其损失函数为

- X 是一个 m 行 n 列的矩阵,其中 m 是数据的数目, n 是特征值的数目
- W是一个 n 行 1 列的矩阵 ,其中 n 是特征的数目
- y 是一个 m 行 1列的矩阵
def Cost_function (theta, X, y):
X_matrix = np.matrix (X)
y_matrix = np.matrix (y).T
temp = np.dot(X_matrix, theta) - y_matrix
J = 1 / 2 * (np.dot (temp.T, temp))
return J通过损失函数对权重参数w进行缩小
我们由损失函数可以知道,权重参数w只决定了损失的大小,如果损失函数为0或接近不变的时候,那么这个时候w也就是最合适的时候,与此同时 损失函数的导数也就为0,那么可以得到下面的式子:

在这里需要强调一下,此时偏导所求的是学习方向,即像哪个方向更新数据
def Update_theta (theta, X, y, num = 150, a = 0.0001):
m, n = X.shape
theta0 = theta[0]
theta1 = theta[1]
x = X[:, -1]
for i in range (num):
pred = x * theta1 + theta0
temp_0 = np.sum(pred - y) / (m)
theta0 = theta0 - a * (temp_0)
temp_1 = np.sum((pred - y) * x) / (m)
theta1 = theta1 - a * (temp_1)
theta[0] = theta0
theta[1] = theta1
return theta
----------