理解PBR：从原理到实现（下）

在前面的文章中我讲了虚幻4中所使用的反射率方程，其中复杂的部分是 Cook-Torrance BRDF，我们把它带入整个积分，回顾一下完整的反射率方程。

$$L_o(p,v)=\underset{H}{\int }(k_d\frac{c_{diff}}{\pi }+k_s\frac{D(h)F(l,h)G(l,v,h)}{4(n\cdot l)(n\cdot v)})L_i(p,l)n\cdot ldl$$

这样复杂的积分是无法求解析解的，只能通过数值计算方法求数值解，在图形领域常用的方法就是“蒙特卡洛积分（Monte Carlo integration）”。对于实时渲染来说，我们还需要祭出我们最常用的两大法宝：预计算和凑合，咳咳，说错了，近似，approximation！我们还需要另外一个重要的技术，就是 IBL，Image Based Lighting！把它们组装起来：把上面这个积分进行恰当的近似，并将能够预计算的部分使用蒙特卡洛积分求出数值解，以贴图的方式存储起来。在实时渲染的时候，通过采样贴图取得这些预计算值，进行 Shading 计算！ 再进一步的说，虚幻4使用 Split Sum Approximation 将上述积分分成两部分进行预计算：

• 一部分的计算结果存储到一个 Cube Map 上，管它叫做“Pre-Filtered Environment Map”；
• 另外一部分的计算结果存储为一张 R16G16 格式的2D贴图，管它叫做：“Environment BRDF”。

【重要提示】 下面的内容需要两个背景知识：蒙特卡洛积分 和 Image Based Lighting，如果你对这两不熟悉，可以先看文章后面一半的基础知识部分。

Split Sum Approximation

下面重点讲一下虚幻4在进行预计算的过程中进行了哪些公式推导和近似。我们先来看一下虚幻4文档中的公式推导的第一步：

$$\underset{H}{\int }{L}_i(p,l)f(l,v)cos{\theta }_{l}dl\approx \frac{1}{N}\sum _{k=1}^N\frac{L_i(l_k)f(l_k,v)cos{\theta }_{l_k}}{p(l_k,v)}$$

这个约等于确不是“凑合”，等式右边就是蒙特卡洛积分公式，其中 $p(l_k,v)$ 就是概率分布函数：pdf，要说明的是：对于渲染方程，pdf 是一个归一化函数（normalized function），即在半球域内的积分值为 1 。 （上面公式中的$cos{\theta }_l$就是我们之前公式中的$n\cdot l$）

接下来，出于性能方面的考虑，下一步是一个颇有道理的近似。

$$\frac{1}{N}\sum _{k=1}^N\frac{L_i(l_k)f(l_k,v)cos{\theta }_{l_k}}{p(l_k,v)}\approx (\frac{1}{N}\sum _{k=1}^N{L}_i(l_k))(\frac{1}{N}\sum _{k=1}^N\frac{f(l_k,v)cos{\theta }_{l_k}}{p(l_k,v)})$$

也就是把第一步的蒙特卡洛公式分拆为两个$\sum$来运算，这样就可以分别进行预计算。这是非常重要的一步，Epic 的大牛给它起了个名字，就叫做：Split Sum Approximation。名字起的很好，就是把一个 $\sum$ 拆分成了 $\sum \cdot \sum$ !这两个 $\sum$ 要分别使用蒙特卡洛积分去计算，并且都使用了重要性采样（Importance Sampling）。重要性采样先单独讲一下。

重要性采样（Importance Sampling）

蒙特卡洛积分的一个焦点就是所谓的“采样（Sampling）”。对于渲染方程，我们能计算的入射光的数量是有限的，所以计算结果和理想积分值会有偏差，也就是会产生渲染结果中的 noise 。另外一方面，我们对渲染方程的行为是有一个粗略的概念的，例如对于非常光滑的表面，那么我们应该在出射光方向（观察方向）的镜面反射方向周围分配更多的样本。这种采样的分布控制就是通过 pdf 函数实现的。

在虚幻4中使用了基于 GGX 分布函数的重要性采样来提高蒙特卡洛积分的精确度。GGX 函数的一个重要参数就是粗糙度。我们可以看一下虚幻4中对应的代码：“Epic Games\UE_4.20\Engine\Shaders\Private\MonteCarlo.ush”，其中 ImportanceSampleGGX(E, a2) 的第一个参数 E，它的取值是 Hammersley Sequence；第二个参数 a2 的取值是粗糙度的四次方。

float4 ImportanceSampleGGX( float2 E, float a2 )
{
	float Phi = 2 * PI * E.x;
	float CosTheta = sqrt( (1 - E.y) / ( 1 + (a2 - 1) * E.y ) );
	float SinTheta = sqrt( 1 - CosTheta * CosTheta );

	float3 H;
	H.x = SinTheta * cos( Phi );
	H.y = SinTheta * sin( Phi );
	H.z = CosTheta;
	
	float d = ( CosTheta * a2 - CosTheta ) * CosTheta + 1;
	float D = a2 / ( PI*d*d );
	float PDF = D * CosTheta;

	return float4( H, PDF );
}

Hammersley Sequence

这里还需要说明一下 Hammersley Sequence，这是一个低差异序列（Low-Discrepancy Sequence），你可以粗略的理解为：它生成一系列分布更为均匀的随机数。下面这个图就是 Hammersley 计算的结果示意图。

下面是它在虚幻4中的实现代码，你可以在“Epic Games\UE_4.20\Engine\Shaders\Private\MonteCarlo.ush”文件中找到它：

float2 Hammersley( uint Index, uint NumSamples, uint2 Random )
{
  float E1 = frac( (float)Index / NumSamples + float( Random.x & 0xffff ) / (1<<16) );
  float E2 = float( ReverseBits32(Index) ^ Random.y ) * 2.3283064365386963e-10;
  return float2( E1, E2 );
}

GGX Distribution

前面讲到虚幻4在蒙特卡洛积分中使用的 pdf 函数是一个基于 GGX 的分布函数，这又是什么意思呢？

我们想要达到的采样分布如上图所示，图中黄色的部分，也就是出射光方向的反射方向，采样更多；黄色区域外的部分采样更少。黄色区域的分布收到物体粗糙度的影响，因为反射向量的分布就是收到微平面的法向量分布影响的！而微平面的法向量分布（其实是$h$向量，说法向量为了更直观），我们在上篇文章中提到了，使用的是 Trowbridge-Reitz GGX 模型。因为 $D(h)$ 是 $h$ 向量的分布，所以 pdf 函数要在它的基础上附加一些计算，就形成了 ImportanceSampleGGX() 函数了！这个公式推导在 Disney 的分享¹中有详细过程，这里就不深究了。

计算Split Sum的第一部分

让我们来聚焦Split Sum的第一部分：

$$\frac{1}{N}\sum _{k=1}^N{L}_i(l_k)$$

这个公式是比较直观的，就是对环境贴图进行卷积，它的计算结果仍然是一个 Cube Map，也就是“Pre-Filtered Environment Map”！

这里有一个问题就是，使用 GGX 概率分布函数的话，需要观察方向V和表面法线N，这两个都是运行时才能得到的，咋整啊？在虚幻4的预计算中，假设 N=V=R ，也就是观察角度为 0！ 这是引入误差最大的一个近似。

虚幻4使用下面这个函数：PrefilterEnvMap()，生成“Pre-Filtered Environment Map”。这个函数有两个参数：粗糙度和反射方向：

1. 每一个 Mip Map Level 对应一个“粗糙度”值；
2. 对于每个 Mip Map Level，每一个贴图像素（texel）就对应一个反射方向；

对于每个 Mip Map Level 上的每个 texel 运行此函数进行卷积，即可得到这部分积分的预计算结果。这个函数计算的过程中用到了Hammersley()和ImportanceSampleGGX()，已经在上面的“重要性采样”一节介绍过了啊。

float3 PrefilterEnvMap(float Roughness, float3 R)
{
    float3 N = R;
    float3 V = R;
    float3 PrefilteredColor = 0;
    const uint NumSamples = 1024;
    for (uint i = 0; i < NumSamples; i++ )
    {
        float2 Xi = Hammersley(i, NumSamples);
        float3 H = ImportanceSampleGGX(Xi, Roughness, N);
        float3 L = 2 * dot(V, H) * H - V;
        float NoL = saturate(dot(N, L));
        if (NoL > 0) {
            PrefilteredColor += EnvMap.SampleLevel(EnvMapSampler, L, 0).rgb * NoL;
            TotalWeight += NoL;
        }
    }
    return PrefilteredColor / TotalWeight;
}

计算Split Sum的第二部分

我们来看一下Split Sum第二部分的公式：

$$\frac{1}{N}\sum _{k=1}^N\frac{f(l_k,v)cos{\theta }_{l_k}}{p(l_k,v)}=\underset{H}{\int }f(l,v)cos{\theta }_{l}dl$$

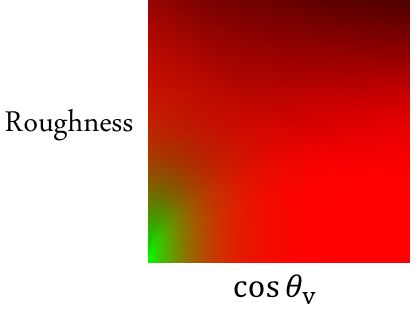
这部分计算的结果就是下面这样一个2D查找表，存储到一个 R16G16 的2D贴图中，叫做“Environment BRDF”。

这个是怎么计算得出的呢？

把 Schlick 菲涅尔近似公式：$F(v,h)=F_0+(1-F_0)(1-v\cdot h{)}^5$ 带入上述积分，发现 $F_0$ 可以从积分中提取出来，Epic 文档中的公式为：

$$\underset{H}{\int }f(l,v)cos{\theta }_{l}dl=F_0\underset{H}{\int }\frac{f(l,v)}{F(v,h)}(1-(1-v\cdot h{)}^5)cos{\theta }_{l}dl+\underset{H}{\int }\frac{f(l,v)}{F(v,h)}(1-v\cdot h{)}^{5}cos{\theta }_{l}dl$$

右侧变为两个积分之后，可以分开求解，输出为两个值：（F_0的缩放, F_0的偏移量），也就是：

$$\underset{H}{\int }f(l,v)cos{\theta }_{l}dl=F_0\cdot EnvBRDF.x+EnvBRDF.y$$

前面的一系列近似之后，这个积分值剩下两个输入变量：粗糙度和 $cos{\theta }_v$，它俩的取值范围都是[0,1]，可以使用下面这个函数计算出一个 2D 查找表，保存到一张贴图中，来提高运行时效率。

float2 IntegrateBRDF(float Roughness, float NoV)
{
    float3 V;
    V.x = sqrt(1.0f - NoV * NoV); // sin
    V.y = 0;
    V.z = NoV; // cos
    float A = 0;
    float B = 0;
    const uint NumSamples = 1024;
    for (uint i = 0; i < NumSamples; i++ )
    {
        float2 Xi = Hammersley(i, NumSamples);
        float3 H = ImportanceSampleGGX(Xi, Roughness, N);
        float3 L = 2 * dot(V, H) * H - V;
        float NoL = saturate(L.z);
        float NoH = saturate(H.z);
        float VoH = saturate(dot(V, H));
        if (NoL > 0) {
            float G = G_Smith(Roughness, NoV, NoL);
            float G_Vis = G * VoH / (NoH * NoV);
            float Fc = pow(1 - VoH, 5);
            A += (1 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    return float2(A, B) / NumSamples;
}

IBL 计算

在运行时，我们就可以通过采样 Pre-Filtered Environment Map 和 Environment BRDF 来进行 IBL 计算了，伪代码如下：

float3 ApproximateSpecularIBL(float3 SpecularColor, float Roughness, float3 N, float3 V)
{
    float NoV = saturate(dot(N, V));
    float3 R = 2 * dot(V, N) * N - V;
    float3 PrefilteredColor = PrefilterEnvMap(Roughness, R);
    float2 EnvBRDF = IntegrateBRDF(Roughness, NoV);
    return PrefilteredColor * (SpecularColor * EnvBRDF.x + EnvBRDF.y);
}

虽然经过了近似，但是就 Epic 的比对来说，结果是很不错的。

---

基础知识

蒙特卡洛积分（Monte Carlo integration）

对于一些复杂的高维定积分，在图形学中通常使用蒙特卡洛方法。蒙特卡洛本是一个地中海城市的名字，是知名的赌城，用这个名字是代表的随机的意思。下面就说一下它的基本思想。

假设我们需要对 $f(x)$ 在 $[a,b]$ 区间内进行积分：

$$F={\int }_a^{b}f(x)dx$$

我们可以使用蒙特卡洛公式来求出它近似的数值解：

$$F^N=\frac{1}{N}\sum _{i=1}^N\frac{f(X_i)}{pdf(X_i)}$$

这个公式的意思就是在指定的范围内随机取 N 个只，并计算出相应的 $f(x)$ 值。这些值的平均值就是对理想积分的一个近似数值解。这里面比较重要的就是 pdf了。pdf 即 probability distribution function，概率分布函数。

Image Based Lighting

渲染方程的直观理解就是：计算空间中任意一点所接收到的所有光线在观察方向上的反射。Image Based Lighting 简称 IBL，可以用来计算场景中一点接收到的场景中其他静态对象产生的光照。把场景中某个点的光照信息，存储到一个 Cube Map 中，就叫做“Light Probe”，虚幻4中叫做“Reflection Capture”，如下图所示。Light Probe 的生成一般是先把这个点周围的场景静态物体渲染到一张环境贴图中（environment map），然后再使用 BRDF 对其进行预计算，形成光照计算所需的数据。在 PBR 中，通常会把不同的“粗糙度”计算结果存储到不同的 Mip Map Level 中。也就是说 Light Probe 的 Cube Map 的 Mip Map 不是传统的贴图的 Mip Map 的概念，而是针对不同“粗糙度”的 BRDF 计算结果。例如，一张有10个 Mip Map Level 的 Cube Map ，每个 Level 对应的就是“粗糙度=0.1*n”。把环境贴图预计算生成 Light Probe 的过程在数学上叫做“卷积（Convolution）”。

理论上，一个 Light Probe 只对应场景中的一个点，而实时渲染中就把一个模型上的所有点都近似的取这个 Light Probe 了。那么，对于空间跨度很大的场景，咱们也不能太“凑合”了！于是，我们可以在场景中的不同位置放置多个 Light Probe，通常是你认为重要的位置，并且可以设置它的体积等参数。在运行时，按照着色的点的位置，对几个 Light Probe 进行插值。这种东西有个名词，叫做“Local Light Probes”。

与 Local Light Probes 对应的就是 “Global Light Probe”。我们可以用一个 Light Probe 对应无限远的光源所产生的环境光，通常就是天空，每个场景可以包含一个 Global Light Probe 。

总结一下：

1. 把场景中的静态环境，或者是天空，存储到一个环境贴图中；
2. 环境贴图中的每个像素可以想象成一个发射间接光的光源；使用 BRDF 对这些小小光源进行预计算，也就是所谓的卷积，从而生成 Light Probe；
3. 在运行时，根据需要着色的点的位置，找到合适的 Local Light Probes(可能是多个)，还有 Global Light Probe；
4. 分别根据粗糙度和反射向量，对这些 Light Probe 进行采样，然后插值；
5. 这个计算结果就是渲染中所需要的环境光反射量。

---

1. Brent Burley, Physically Based Shading at Disney, SIGGRAPH 2012 ↩︎