4.3.1有监督学习(六) - 朴素贝叶斯分类(Naive Bayesian Classifier)
简介
贝叶斯分类方法是与有监督学习中的最直观简单的方法。贝叶斯分类器缘起于贝叶斯定理,在定理的基础上发展为了朴素贝叶斯分类法(Naive Bayesian Classification)。朴素贝叶斯分类方法的好处在于简单直接,它一般用于概率推理与决策,即在信息不全的时候,通过观察随机变量,推断不可观察的随机变量。
一句话解释版本:
贝叶斯分类是利用概率论作为基础推断不可观测变量的类别,其基础原理是贝叶斯定理,后续还发展出了贝叶斯网络。
数据分析与挖掘体系位置
贝叶斯分类器是有监督学习中的一种模型。所以在数据分析与数据挖掘中的位置如下图所示。
贝叶斯定理
朴素贝叶斯、贝式网络、贝叶斯分类器,这些词汇与背后算法的理论基础都是贝叶斯定理。
贝叶斯理论是通过历史的经验来判断新的事物所具有的特征。为什么贝叶斯理论应用很广呢?举个例子说吧,你如果知道一个人感冒了,你很容易推测她咳嗽的概率。但是,如果你知道一个人咳嗽,让你反过来推测她得的病是感冒的概率,则会相对困难。而贝叶斯理论正是在解决这个问题。
首先,我们把一个人咳嗽称为事件A,把一个人感冒称为事件B。
那么,贝叶斯公式就是:
其中,
- P(A|B)被称为条件概率,即在B事件发生的条件下,A事件发生的概率。
- P(AB)称为联合概率,即事件A与事件B共同发生的概率。
- P(A)与P(B)是先验概率,分别是事件A与事件B发生的概率。
上面的公式成立需要满足一个条件,就是A与B要相互独立。也就是说A的发生与B的发生没有关系。在A与B独立的情况下,贝叶斯定理发挥的效果最好,但是这一点在现实中非常难满足,所以也是贝叶斯定理的局限性。后期发展出的贝叶斯网络就是在弥补这个缺陷。
朴素贝叶斯的数学原理
朴素贝叶斯是直接应用贝叶斯定理延展出的分类器。我们以之前说过的“去不去玩”的案例来演示一下其分类过程。
首先,数据源如下:
数据源分为特征矩阵(feature matrix)和响应向量(response vector)。
- 特征矩阵是数据中自变量的每一行。特征就是自变量。
- 响应向量是数据中因变量的每一行。相应就是因变量。因为Y只有一列,所以称为向量。
基本公式与假设
同样是上述公式,在这个情景中贝叶斯定理可以被解释为:
其中:
- P(y|X)是已知“加班”,“双休日”,“女朋友意愿”与“天气”结果的情况下,“去不去玩”结果的概率
- P(X|y)是已知“去不去玩”结果的情况下,“加班”,“双休日”,“女朋友意愿”与“天气”各个结果的概率
上面提到的假设同样存在。所以,贝叶斯定理假设各个自变量之间相互独立。“加班”与“是否双休日”与“天气”与“女朋友意愿”之间都没有任何关系。谁也不能影响谁。当然,这个肯定不满足,所以自然贝叶斯分类器的效果也会受到干扰。
朴素贝叶斯推导
尽管假设不满足,我们仍然可以进行贝叶斯分类。而我们现在的问题变成了:通过“加班”,“双休日”,“女朋友意愿”与“天气”结果,推算“去不去玩”的概率。即求P(y|X),再直白点,就是求P(去玩|加班、是双休日、女朋友ok,晴天)...等的概率。
所以,上面的贝叶斯公式就变成了:
由于“加班”、“是否双休日”、“天气”、“女朋友意愿”这些特征之间相互独立。所以:
所以,最终,公式就变成了:
把这个拓展到数学公式上就是:
上面公式得到的结果,是y取某个决策的概率。
如果Y有TRUE/FALSE两种取值结果,我们会比较P(y=1|X)的概率与P(y=0|X)的概率那个更大。朴素贝叶斯最终预测的结果是概率更大的那一个。
实例计算
假如我们需要预测:在不加班、不是双休日、女友OK、多云的情况下,决策我们最终会不会出去玩。
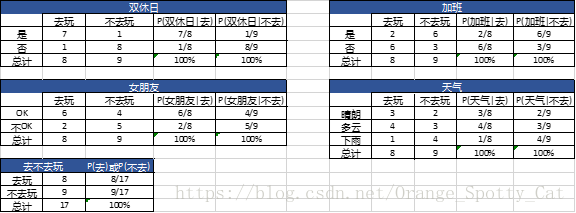
这时,通过已有的17个样本数据,我们能够得到如下概率:
所以,将这些概率值代入公式中,就能得到:
由于P(去玩|X) + P(不去玩|X) = 1,且分母一样。
所以解二元一次方程可以得到:P(去玩|X) = 0.4156,P(不去玩|X) = 0.5844.
不去玩的概率要大于去玩的概率。所以我们的决策结果是:不出去玩。
朴素贝叶斯在R上的实现
rm(list=ls())
# 读取数据,原数据在github中https://github.com/starsfell
setwd('C:/Users/xintong.yan/Desktop')
df <- read.table('sample_data.txt',header = T)
# 上述案例
test <- list('否','否','OK','多云')
library(e1071)
# 建模
naive_bay <- naiveBayes(Result~SXR+JB+NPY+TQ, df, laplace = 0)
# 预测
test_result <- predict(naive_bay, test, type="class")