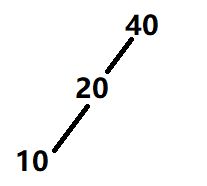树——AVL树
文章目录
- AVL树(BST树的优化和改进)
- AVL树代码
AVL树(BST树的优化和改进)
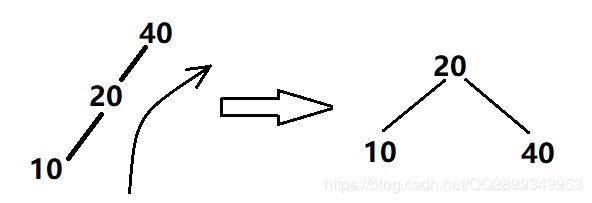
BST树最差的情况下,就退化成一条链表了,增删查的时间复杂度就无法达到O( log 2 n \log_2n log2n) ,AVL树在BST的基础上,加入了节点左右子树高度差的概念,就是任意一个节点的左子树和右子树的高度差不能超过1,就说这颗树是一颗平衡树,否则就要通过既定规则的旋转操作,使排序树达到平衡的状态。
AVL就是满足上面条件所述的一颗二叉平衡树,AVL树中每一个节点的左右子树高度差不能超过1,所以对应会有四种情况不满足AVL树,下面是四种情况以及使他们重新平衡的处理方法(旋转);
为了达到平衡,AVL进行的四种旋转操作:
-
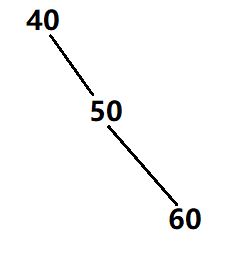
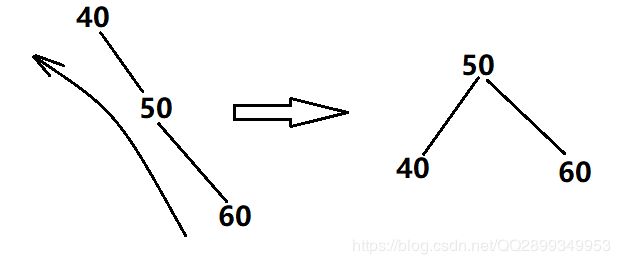
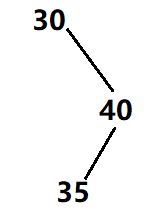
左孩子的右子树太高了:

这个时候,要想维护平衡,单纯的一次旋转已经不能维护平衡了,比如,只进行一次右旋:
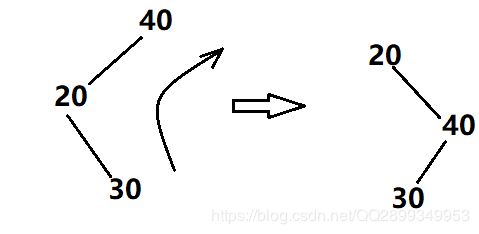
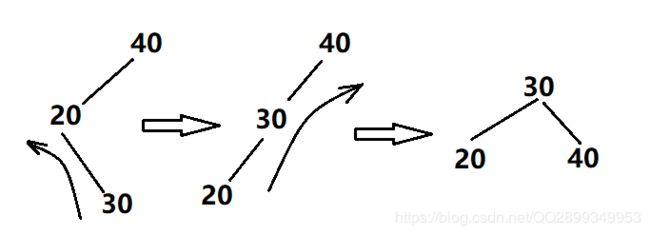
这样还是不平衡,所以这个时候是需要两次旋转的,当左孩子的右子树太高了的时候,需要先左旋后右旋,即左—右旋转,也叫左平衡:
AVL树代码
/**
* @ClassName AVLNode
* @Description AVL树节点
* @Author lzq
* @Date 2019/7/5 23:35
* @Version 1.0
**/
public class AVLNode> {
private T data;
private int height; //用来记录树的高度
private AVLNode left;
private AVLNode right;
public AVLNode(T data, int height) {
this.data = data;
this.height = height;
}
public AVLNode(T data, int height, AVLNode left, AVLNode right) {
this.data = data;
this.height = height;
this.left = left;
this.right = right;
}
public T getData() {
return data;
}
public int getHeight() {
return height;
}
public AVLNode getLeft() {
return left;
}
public AVLNode getRight() {
return right;
}
public void setData(T data) {
this.data = data;
}
public void setHeight(int height) {
this.height = height;
}
public void setLeft(AVLNode left) {
this.left = left;
}
public void setRight(AVLNode right) {
this.right = right;
}
}
import java.util.LinkedList;
/**
* @ClassName AVL
* @Description AVL树
* @Author lzq
* @Date 2019/7/5 23:38
* @Version 1.0
**/
public class AVL> {
private AVLNode root; //根节点指针
/**
* 获取节点node的左右子树的高度差
* @param node
* @return
*/
private int height(AVLNode node) {
return node == null ? 0 : node.getHeight();
}
/**
* 返回当前节点左右子树的高度最高值
* @param left
* @param right
* @return
*/
private int maxHeight(AVLNode left,AVLNode right) {
return height(left) > height(right) ? height(left) : height(right);
}
/**
* AVL的右旋操作;
* 节点的左右子树失衡,是由于左孩子的左子树太高造成的
* 40
* / 右旋 30
* 30 =====> / |
* / 20 40
* 20
* @param node
* @return
*/
private AVLNode rotateRight(AVLNode node) {
AVLNode child = node.getLeft();
node.setLeft(child.getRight());
child.setRight(node);
node.setHeight(maxHeight(node.getLeft(),node.getRight())+1);
child.setHeight(maxHeight(child.getRight(), child.getLeft())+1);
return child;
}
/**
* 左旋
* 右孩子右子树太高
* 20
* \ 左旋 30
* 30 =======> / \
* \ 20 40
* 40
* @param node
* @return
*/
private AVLNode rotateLeft(AVLNode node) {
AVLNode child = node.getRight();
node.setRight(child.getLeft());
child.setLeft(node);
node.setHeight(maxHeight(node.getLeft(),node.getRight())+1);
child.setHeight(maxHeight(child.getRight(), child.getLeft())+1);
return child;
}
/**
* 左—右旋转
* 左孩子的右子树太高
* 50 50
* / 对左子树左旋 / 右旋 40
* 30 ===========> 40 ======> / \
* \ / 30 50
* 40 30
* @param node
* @return
*/
private AVLNode leftBalance(AVLNode node) {
node.setLeft(rotateLeft(node.getLeft())); //先对它左孩子进行左旋
return rotateRight(node); //自己再右旋
}
/**
* 右左旋转
* 右孩子的左子树太高
* 30 30
* \ 对右子树左旋 \ 左旋 40
* 50 ===========> 40 ===> / \
* / \ 30 50
* 40 50
* @param node
* @return
*/
private AVLNode rightBalance(AVLNode node) {
node.setRight(rotateRight(node.getRight()));
return rotateLeft(node);
}
/**
* 插入节点
* @param data
*/
public void insert(T data) {
if(root == null) {
root = new AVLNode(data,1);
return;
}
root = addAVLNode(root,data);
}
private AVLNode addAVLNode(AVLNode root, T data) {
if(root == null) {
return new AVLNode(data,1);
}
if(root.getData().compareTo(data) > 0) {
AVLNode node = addAVLNode(root.getLeft(),data);
root.setLeft(node);
//左子树太高
if(height(root.getLeft()) - height(root.getRight()) > 1) {
//左孩子的左子树太高
if(height(root.getLeft().getLeft()) > height(root.getLeft().getRight())) {
root = rotateRight(root); //一旋转根就变了
}
//左孩子的右子树太高
else {
root = leftBalance(root);
}
}
}
if(root.getData().compareTo(data) < 0) {
AVLNode node = addAVLNode(root.getRight(),data);
root.setRight(node);
//右孩子太高
if(height(root.getRight()) - height(root.getLeft()) > 1) {
//右孩子的右子树太高
if(height(root.getRight().getRight()) > height(root.getRight().getLeft())) {
root = rotateLeft(root);
}
//右孩子的左子树太高
else {
root = rightBalance(root);
}
}
}
//递归回溯过程中更新节点的高度值
root.setHeight(maxHeight(root.getLeft(),root.getRight())+1);
return root;
}
/**
* 层序遍历
*/
public void show() {
if(root == null) {
return;
}
LinkedList> list = new LinkedList<>();
list.addLast(root);
int sign = 1;
int count = 0;
while (list.size() > 0) {
AVLNode node = list.pollFirst();
System.out.print(node.getData()+":"+node.getHeight()+"\t");
if(node.getLeft() != null) {
list.addLast(node.getLeft());
count++;
}
if(node.getRight() != null) {
list.addLast(node.getRight());
count++;
}
sign--;
if(sign == 0) {
sign = count;
count = 0;
System.out.println();
}
}
System.out.println("-----------------------");
}
/**
* 删除指定节点
* @param data
*/
public void remove(T data) {
this.root = delete(root,data);
}
private AVLNode delete(AVLNode root, T data) {
if(root == null) {
return null;
}
if(root.getData().compareTo(data) > 0){
root.setLeft(delete(root.getLeft(), data));
//右子树太高
if(height(root.getRight()) - height(root.getLeft()) > 1) {
//右孩子的右子树太高
if(height(root.getRight().getRight()) >= height(root.getRight().getLeft())) {
root = rotateLeft(root);
}
//右孩子的左子树太高
else {
root = rightBalance(root);
}
}
} else if(root.getData().compareTo(data) < 0){
root.setRight(delete(root.getRight(), data));
//左子树太高
if(height(root.getLeft()) - height(root.getRight()) > 1) {
//左子树的左孩子太高
if (height(root.getLeft().getLeft()) > height(root.getLeft().getRight())) {
root = rotateRight(root);
}
//左子树的右孩子太高
else {
root = leftBalance(root);
}
}
} else {
if(root.getLeft() != null && root.getRight() != null){
//左右子树哪个高删除哪个,减少旋转,提高效率
if(height(root.getLeft()) >= height(root.getRight())) {
//用前驱替换
AVLNode pre = root;
pre = pre.getLeft();
while(pre.getRight() != null){
pre = pre.getRight();
}
root.setData(pre.getData());
root.setLeft(delete(root.getLeft(), pre.getData()));
}else {
//用后继替换
AVLNode pre = root;
pre = pre.getRight();
while(pre.getLeft() != null){
pre = pre.getLeft();
}
root.setData(pre.getData());
root.setRight(delete(root.getRight(), pre.getData()));
}
} else {
if(root.getLeft() != null){
return root.getLeft();
} else if(root.getRight() != null){
return root.getRight();
} else {
return null;
}
}
}
root.setHeight(maxHeight(root.getLeft(),root.getRight())+1);
return root;
}
/**
* 查找指定值的节点
* @param data
* @return
*/
public T findNode(T data) {
return find(root,data);
}
private T find(AVLNode root, T data) {
if(root == null) {
return null;
}
if(root.getData().compareTo(data) == 0) {
return root.getData();
}else if(root.getData().compareTo(data) < 0) {
return find(root.getRight(),data);
}else {
return find(root.getLeft(),data);
}
}
}
测试代码:
public static void main(String[] args) {
AVL avl = new AVL<>();
for (int i = 1; i <= 10; i++) {
avl.insert(i);
}
avl.show();
avl.remove(8);
avl.show();
avl.remove(4);
avl.show();
System.out.println(avl.findNode(7));
System.out.println(avl.findNode(12));
}
运行结果:
4:4
2:2 8:3
1:1 3:1 6:2 9:2
5:1 7:1 10:1
-----------------------
4:4
2:2 7:3
1:1 3:1 6:2 9:2
5:1 10:1
-----------------------
5:4
2:2 7:3
1:1 3:1 6:1 9:2
10:1
-----------------------
7
null