读论文之《基于 FPGA 的并行全比较排序算法》
为什么介绍这种排序算法:最近在独立编写霍夫曼编码的verilog HDL设计程序,其中用到了排序模块,对一组数据进行排序,苦寻几天,最终找到了这个全新的适合硬件实现的排序算法,分享与此,以空间换时间的并行排序算法。十分感谢论文作者,看到这样的方法,我太激动了。
并行全比较排序算法介绍:
排序是一种重要的数据运算,传统的排序方法主要靠软件串行方式实现,包括冒泡法、选择法、计数法等,这些算法大多采用循环比较,运算费时,实时性差。不能满足工程上越来越高的实时性要求。实时性排序在工程计算中的要求越来越迫切。本文基于FPGA的硬件特点,提出了一种全新的并行全比较排序算法,又可被称为“以空间换时间”并行排序算法,可大幅提高数据处理的实时性。
并行全比较排序算法原理:
一组数据,先进行两两之间的比较,每两个数比较都会得到一个比较结果。可以根据两数的大小定义输出排序结果0或1。对这些比较结果进行累加计算,即可得到该数在序列中的排序值。由于所有数的两两之间的比较都在硬件内同时进行,只需一个时钟的时间,即可得到比较结果,再加上比较结果的和加等计算时间,几个时钟周期,就实现了数字序列的排序。
实例介绍:
假设有一数组{20,80,40,40,60,70}, 定为A0=20、A1=80、A2=40、A3=40、A4=60、A5=70,要求对该数组按从大到小的顺序排列。排序按以下过程进行:
输入比较器的选取(认真读懂):
要进行数据之间的两两比较,首先要确定比较器。考虑到数组中有相同数据,并且后续还要进行和加计算。数据相同的排序按照原数据谁在前谁优先原则,要实现这种原则下的排序,在每个数据与其它数据比较时,根据两个数字原来在数组中的顺序,比较器的类型要发生变化。比如Am和其它数比较时,在与数An比较时:
如果m>n,则选用“≥”比较器;
如果m
注意:为什么一会采用不同的比较器类型,是因为数据相同的排序按照原数据谁在前谁优先原则,采用上述比较器规定的类型,恰好解决这个问题。事实上,个人认为用一种类型的比较器也行,数据相同的排序,谁在前在后应该是无所谓的。
进行各数之间的比较
为了后续的计算,先作统一规定,如果数Am和数An相比较,如果Am≥An(或Am>An),则比较结果Z=1;否则,则Z=0。
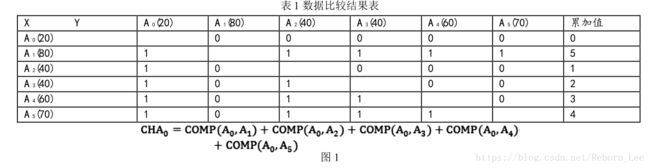
各数之间比较结果如下表:
比较结果累加计算
各数字两两比较后,对与一个数相比较的所有值的结果相加(COMP(X,Y)为比较器),以A0为例,其对应的比较累加和为:![]()
由表可知计算结果,CHA0=0,在序列中从大到小的顺序为0(数列的最大值排序为第5位),也即是在序列中为最小值。同样,A1、A2、A3、A4、A5 的比较值累加和分别为CH A1=5,CH A2=1,CH A3=2;CH A4=3,CH A5=4。那么,各数字在数组中的排序位置已经确定,各值从大到小排列为:A1、A5、A4、A3、A2、A0。
排序结果输出
各数字的排序位置确定后,要把排序结果输出。
算法基于verilog HDL语言描述:
排序算法在FPGA内进行,实现过程主要有以下几步,采用verilog语言来描述:
(1)第一个时钟周期,数据全比较程序,6个数据排序,输入数据为in0~in5:
//in0和其他数据进行比较
if(in0>in1) a0<=1; else a0<=0;
if(in0>in2) a1<=1; else a1<=0;
if(in0>in3) a2<=1; else a2<=0;
⋯⋯
//in1和其他数据进行比较
if(in1>in0) b0<=1; else b0<=0;
if(in1>in2) b1<=1; else b1<=0;
if(in1>in3) b2<=1; else b2<=0;
⋯⋯
//in2和其他数据进行比较
if(in2>in0) c0<=1; else c0<=0;
if(in2>in1) c1<=1; else c1<=0;
if(in2>in3) c2<=1; else c2<=0;
⋯⋯
(2)第二个时钟周期,比较值累加,mid0、mid1、mid2等为比较累
加值
mid0<=a0+a1+a2+a3+a4;
mid1<=b0+b1+b2+b3+b4;
mid2<=c0+c1+c2+c3+c4;
⋯⋯
(3)第三个时钟周期,把输入值赋给其对应的排序空间
chn[mid0]=in0;
chn[mid1]=in1;
chn[mid2]=in2;
⋯⋯
(4)第四个时钟周期,把排序结果输出
out 0<=chn[0]; //最小值
out 1<= chn[1]; //次小值
out 2<= chn[2];
⋯⋯
经过以上几个步骤,算法完成,整个算法共需要4个时钟周期。
并行全比较排序性能分析:
空间复杂性
由于并行全比较排序算法需要全并行处理,因此占用了大量的处理空间,又可称之为“空间换时间”排序算法。经计算统计,如果需
要排序的总数字个数为n,则并行排序算法所需要的比较器为(n-1)的2次方个,每个比较器在FPGA中设计占用逻辑单元为5个左右,那么排序需要的逻辑单元为5×(n-1)的2次方个。
时间复杂性
在FPGA内实现并行全比较算法,只需4个时钟周期就可实现排序计算。时间复杂度为定值。如果FPGA的时钟周期为10ns,那么整
个排序算法时间只有40ns。而传统的排序算法比如冒泡法,时间复杂度为n(n-1)/2,按照时钟周期10ns计算,100个数的冒泡排序时间可49.5μs,远远大于并行排序算法时间,这其中还不包括相关循环计算时间。
结论:
从上述论述可知,全比较排序算法基于FPGA技术,实现数据排序并行处理,排序运算只需要几个时钟的运算时间,并且运算时间不随排序数据量变化,达到了实时性排序的效果。该算法具有通用性,可以应用到各种数据快速排序运算领域。
对10个数进行并行排序,正式给出verilog HDL设计代码:
//对10个数进行并行排序
module sort_paralell(clk, rst, in0, in1, in2, in3, in4, in5, in6, in7,
in8, in9, out0, out1, out2, out3, out4, out5, out6,
out7, out8, out9);
input clk;
input rst;
input [7:0] in0, in1, in2, in3, in4, in5, in6, in7, in8, in9;
reg [7:0] out_temp[9:0];//输出数据放入此数组中
output [7:0] out0, out1, out2, out3, out4, out5, out6, out7, out8, out9;
reg [7:0] out0, out1, out2, out3, out4, out5, out6, out7, out8, out9;
//下面定义的变量用于存储比较结果,如in0 > in1,则a0 <= 1,否则a0 <= 0;
reg a0, a1, a2, a3, a4, a5, a6, a7, a8;
reg b0, b1, b2, b3, b4, b5, b6, b7, b8;
reg c0, c1, c2, c3, c4, c5, c6, c7, c8;
reg d0, d1, d2, d3, d4, d5, d6, d7, d8;
reg e0, e1, e2, e3, e4, e5, e6, e7, e8;
reg f0, f1, f2, f3, f4, f5, f6, f7, f8;
reg g0, g1, g2, g3, g4, g5, g6, g7, g8;
reg h0, h1, h2, h3, h4, h5, h6, h7, h8;
reg i0, i1, i2, i3, i4, i5, i6, i7, i8;
reg j0, j1, j2, j3, j4, j5, j6, j7, j8;
reg add_start; //该变量的作用是判断比较是否结束,比较结束后赋值为1,进入相加模块
reg assignm_start; //该变量作用在于判断相加模块执行是否结束,结束后赋值为1,进入下一个输出模块
//下面定义的变量用于存储上述中间变量累加结果,9个1位2进制数相加最多4位
reg out_start;
reg [3:0] mid0, mid1, mid2, mid3, mid4, mid5, mid6, mid7, mid8, mid9;
//并行比较模块(第一个时钟)
always @ (posedge clk)
begin
if(rst)
begin
{a0, a1, a2, a3, a4, a5, a6, a7, a8} <= 9'b0000_0000_0;
{b0, b1, b2, b3, b4, b5, b6, b7, b8} <= 9'b0000_0000_0;
{c0, c1, c2, c3, c4, c5, c6, c7, c8} <= 9'b0000_0000_0;
{d0, d1, d2, d3, d4, d5, d6, d7, d8} <= 9'b0000_0000_0;
{e0, e1, e2, e3, e4, e5, e6, e7, e8} <= 9'b0000_0000_0;
{f0, f1, f2, f3, f4, f5, f6, f7, f8} <= 9'b0000_0000_0;
{g0, g1, g2, g3, g4, g5, g6, g7, g8} <= 9'b0000_0000_0;
{h0, h1, h2, h3, h4, h5, h6, h7, h8} <= 9'b0000_0000_0;
{i0, i1, i2, i3, i4, i5, i6, i7, i8} <= 9'b0000_0000_0;
{j0, j1, j2, j3, j4, j5, j6, j7, j8} <= 9'b0000_0000_0;
{mid0, mid1, mid2, mid3, mid4, mid5, mid6, mid7, mid8, mid9} <=
40'b0000_0000_0000_0000_0000_0000_0000_0000_0000_0000;
out0 <= 0; out1 <= 0; out2 <= 0; out3 <= 0;out4 <= 0; out5 <= 0;
out6 <= 0; out7 <= 0;out8 <= 0; out9 <= 0;
add_start <= 0;
assignm_start <= 0;
out_start <= 0;
end
else
begin
if(in0 > in1) a0 <= 1'b1; //in0和所有除自己外的其他数据比较,大于则标志置1
else a0 <= 1'b0;
if(in0 > in2) a1 <= 1'b1;
else a1 <= 1'b0;
if(in0 > in3) a2 <= 1'b1;
else a2 <= 1'b0;
if(in0 > in4) a3 <= 1'b1;
else a3 <= 1'b0;
if(in0 > in5) a4 <= 1'b1;
else a4 <= 1'b0;
if(in0 > in6) a5 <= 1'b1;
else a5 <= 1'b0;
if(in0 > in7) a6 <= 1'b1;
else a6 <= 1'b0;
if(in0 > in8) a7 <= 1'b1;
else a7 <= 1'b0;
if(in0 > in9) a8 <= 1'b1;
else a8 <= 1'b0;
if(in1 > in0) b0 <= 1'b1;//in1和所有除自己外的数据比较,大于标志位置1,否则为0
else b0 <= 1'b0;
if(in1 > in2) b1 <= 1'b1;
else b1 <= 1'b0;
if(in1 > in3) b2 <= 1'b1;
else b2 <= 1'b0;
if(in1 > in4) b3 <= 1'b1;
else b3 <= 1'b0;
if(in1 > in5) b4 <= 1'b1;
else b4 <= 1'b0;
if(in1 > in6) b5 <= 1'b1;
else b5 <= 1'b0;
if(in1 > in7) b6 <= 1'b1;
else b6 <= 1'b0;
if(in1 > in8) b7 <= 1'b1;
else b7 <= 1'b0;
if(in1 > in9) b8 <= 1'b1;
else b8 <= 1'b0;
if(in2 > in0) c0 <= 1'b1;
else c0 <= 1'b0;
if(in2 > in1) c1 <= 1'b1;
else c1 <= 1'b0;
if(in2 > in3) c2 <= 1'b1;
else c2 <= 1'b0;
if(in2 > in4) c3 <= 1'b1;
else c3 <= 1'b0;
if(in2 > in5) c4 <= 1'b1;
else c4 <= 1'b0;
if(in2 > in6) c5 <= 1'b1;
else c5 <= 1'b0;
if(in2 > in7) c6 <= 1'b1;
else c6 <= 1'b0;
if(in2 > in8) c7 <= 1'b1;
else c7 <= 1'b0;
if(in2 > in9) c8 <= 1'b1;
else c8 <= 1'b0;
if(in3 > in0) d0 <= 1'b1;
else d0 <= 1'b0;
if(in3 > in1) d1 <= 1'b1;
else d1 <= 1'b0;
if(in3 > in2) d2 <= 1'b1;
else d2 <= 1'b0;
if(in3 > in4) d3 <= 1'b1;
else d3 <= 1'b0;
if(in3 > in5) d4 <= 1'b1;
else d4 <= 1'b0;
if(in3 > in6) d5 <= 1'b1;
else d5 <= 1'b0;
if(in3 > in7) d6 <= 1'b1;
else d6 <= 1'b0;
if(in3 > in8) d7 <= 1'b1;
else d7 <= 1'b0;
if(in3 > in9) d8 <= 1'b1;
else d8 <= 1'b0;
if(in4 > in0) e0 <= 1'b1;
else e0 <= 1'b0;
if(in4 > in1) e1 <= 1'b1;
else e1 <= 1'b0;
if(in4 > in2) e2 <= 1'b1;
else e2 <= 1'b0;
if(in4 > in3) e3 <= 1'b1;
else e3 <= 1'b0;
if(in4 > in5) e4 <= 1'b1;
else e4 <= 1'b0;
if(in4 > in6) e5 <= 1'b1;
else e5 <= 1'b0;
if(in4 > in7) e6 <= 1'b1;
else e6 <= 1'b0;
if(in4 > in8) e7 <= 1'b1;
else e7 <= 1'b0;
if(in4 > in9) e8 <= 1'b1;
else e8 <= 1'b0;
if(in5 > in0) f0 <= 1'b1;
else f0 <= 1'b0;
if(in5 > in1) f1 <= 1'b1;
else f1 <= 1'b0;
if(in5 > in2) f2 <= 1'b1;
else f2 <= 1'b0;
if(in5 > in3) f3 <= 1'b1;
else f3 <= 1'b0;
if(in5 > in4) f4 <= 1'b1;
else f4 <= 1'b0;
if(in5 > in6) f5 <= 1'b1;
else f5 <= 1'b0;
if(in5 > in7) f6 <= 1'b1;
else f6 <= 1'b0;
if(in5 > in8) f7 <= 1'b1;
else f7 <= 1'b0;
if(in5 > in9) f8 <= 1'b1;
else f8 <= 1'b0;
if(in6 > in0) g0 <= 1'b1;
else g0 <= 1'b0;
if(in6 > in1) g1 <= 1'b1;
else g1 <= 1'b0;
if(in6 > in2) g2 <= 1'b1;
else g2 <= 1'b0;
if(in6 > in3) g3 <= 1'b1;
else g3 <= 1'b0;
if(in6 > in4) g4 <= 1'b1;
else g4 <= 1'b0;
if(in6 > in5) g5 <= 1'b1;
else g5 <= 1'b0;
if(in6 > in7) g6 <= 1'b1;
else g6 <= 1'b0;
if(in6 > in8) g7 <= 1'b1;
else g7 <= 1'b0;
if(in6 > in9) g8 <= 1'b1;
else g8 <= 1'b0;
if(in7 > in0) h0 <= 1'b1;
else h0 <= 1'b0;
if(in7 > in1) h1 <= 1'b1;
else h1 <= 1'b0;
if(in7 > in2) h2 <= 1'b1;
else h2 <= 1'b0;
if(in7 > in3) h3 <= 1'b1;
else h3 <= 1'b0;
if(in7 > in4) h4 <= 1'b1;
else h4 <= 1'b0;
if(in7 > in5) h5 <= 1'b1;
else h5 <= 1'b0;
if(in7 > in6) h6 <= 1'b1;
else h6 <= 1'b0;
if(in7 > in8) h7 <= 1'b1;
else h7 <= 1'b0;
if(in7 > in9) h8 <= 1'b1;
else h8 <= 1'b0;
if(in8 > in0) i0 <= 1'b1;
else i0 <= 1'b0;
if(in8 > in1) i1 <= 1'b1;
else i1 <= 1'b0;
if(in8 > in2) i2 <= 1'b1;
else i2 <= 1'b0;
if(in8 > in3) i3 <= 1'b1;
else i3 <= 1'b0;
if(in8 > in4) i4 <= 1'b1;
else i4 <= 1'b0;
if(in8 > in5) i5 <= 1'b1;
else i5 <= 1'b0;
if(in8 > in6) i6 <= 1'b1;
else i6 <= 1'b0;
if(in8 > in7) i7 <= 1'b1;
else i7 <= 1'b0;
if(in8 > in9) i8 <= 1'b1;
else i8 <= 1'b0;
if(in9 > in0) j0 <= 1'b1;
else j0 <= 1'b0;
if(in9 > in1) j1 <= 1'b1;
else j1 <= 1'b0;
if(in9 > in2) j2 <= 1'b1;
else j2 <= 1'b0;
if(in9 > in3) j3 <= 1'b1;
else j3 <= 1'b0;
if(in9 > in4) j4 <= 1'b1;
else j4 <= 1'b0;
if(in9 > in5) j5 <= 1'b1;
else j5 <= 1'b0;
if(in9 > in6) j6 <= 1'b1;
else j6 <= 1'b0;
if(in9 > in7) j7 <= 1'b1;
else j7 <= 1'b0;
if(in9 > in8) j8 <= 1'b1;
else j8 <= 1'b0;
add_start <= 1; //比较结束标志,相加开始标志
end
end
//相加模块,mid(i)的值代表着in(i)所在输出数组中的位置,(第二个时钟)
always @ (posedge clk)
begin
if(add_start == 1)
begin
mid0 <= a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8; //标志位相加,所得结果就是其所在位置
mid1 <= b0 + b1 + b2 + b3 + b4 + b5 + b6 + b7 + b8;
mid2 <= c0 + c1 + c2 + c3 + c4 + c5 + c6 + c7 + c8;
mid3 <= d0 + d1 + d2 + d3 + d4 + d5 + d6 + d7 + d8;
mid4 <= e0 + e1 + e2 + e3 + e4 + e5 + e6 + e7 + e8;
mid5 <= f0 + f1 + f2 + f3 + f4 + f5 + f6 + f7 + f8;
mid6 <= g0 + g1 + g2 + g3 + g4 + g5 + g6 + g7 + g8;
mid7 <= h0 + h1 + h2 + h3 + h4 + h5 + h6 + h7 + h8;
mid8 <= i0 + i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8;
mid9 <= j0 + j1 + j2 + j3 + j4 + j5 + j6 + j7 + j8;
end
assignm_start <= 1;//相加结束,赋值开始标志
end
//输出模块,将排序好的数据放入输出数组中(第三个时钟)
always @ (posedge clk)
begin
if(assignm_start == 1)
begin
out_temp[mid0] <= in0;
out_temp[mid1] <= in1;
out_temp[mid2] <= in2;
out_temp[mid3] <= in3;
out_temp[mid4] <= in4;
out_temp[mid5] <= in5;
out_temp[mid6] <= in6;
out_temp[mid7] <= in7;
out_temp[mid8] <= in8;
out_temp[mid9] <= in9;
out_start <= 1;//赋值结束,输出开始标志位
end
end
always @ (posedge clk)
begin
if(out_start == 1)
begin
out0 <= out_temp[0];
out1 <= out_temp[1];
out2 <= out_temp[2];
out3 <= out_temp[3];
out4 <= out_temp[4];
out5 <= out_temp[5];
out6 <= out_temp[6];
out7 <= out_temp[7];
out8 <= out_temp[8];
out9 <= out_temp[9];
end
end
endmodule测试文件为:
`timescale 1ns/1ps;
module sort_paralell_tb;
reg clk, rst;
reg [7:0] din0, din1, din2, din3, din4, din5, din6, din7, din8, din9;
wire [7:0] dout0, dout1, dout2, dout3, dout4, dout5, dout6, dout7, dout8, dout9;
always
begin
#10 clk = ~clk;
end
initial
begin
clk = 1'b0;
rst = 1'b1;
din0 = 20; din1 = 25; din2 = 52; din3 = 32; din4 = 12;
din5 = 98; din6 = 44; din7 = 8; din8 = 86; din9 = 22;
#10 rst = 1'b0;
end
sort_paralell u1(.clk(clk), .rst(rst), .in0(din0), .in1(din1), .in2(din2),
.in3(din3), .in4(din4), .in5(din5), .in6(din6), .in7(din7),
.in8(din8), .in9(din9), .out0(dout0), .out1(dout1), .out2(dout2),
.out3(dout3), .out4(dout4), .out5(dout5), .out6(dout6), .out7(dout7),
.out8(dout8), .out9(dout9));
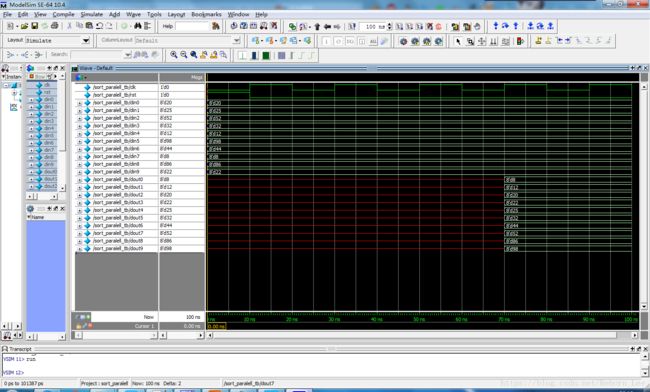
endmodule在Modelsim中仿真所得结果为:
放大图:
完美排序,只需要4个时钟周期。
心得:互联网上的东西杂乱不堪,几乎没有一个博客能够把问题讲的清清楚楚,更很少有有贴出代码的。
把一个问题从头到尾搞的清清楚楚的,并给出自己的总结,这是我们搞研究的人最最开心的事,希望秉持这种态度,继续提升自己。
找到这个论文不容易,首先真心感激作者创新型的想法,尽管论文当中也有一些错误的地方,但本人根据自己的理解,在博客中作出了改正,并写出了verilog HDL设计代码,以及测试代码,在Modelsim中仿真的也很成功。事实上,写这个排序算法的硬件实现并不是目的,目的是接下来的哈弗曼编码的Verilog HDL实现,排序算法是其中的一个模块。