【阅读笔记】《Fully Convolutional Networks for Semantic Segmentation》(FCN)
本文记录了博主阅读论文《Fully Convolutional Networks for Semantic Segmentation》的笔记,代码。更新于2019.04.16。
文章目录
- 摘要
- Introduction
- Related work
- Fully convolutional networks
- Adapting classifiers for dense prediction
- Shift-and-stitch is filter rarefaction
- Upsampling is backwards strided convolution
- Patchwise training is loss sampling
- Segmentation Architecture
- From classifier to dense FCN
- Combining what and where
- Experimental framework
- Results
- Conclusion
摘要
Introduction
Related work
Fully convolutional networks
卷积网络(Convnet)中的每个层都是一个尺寸为 h × w × d h\times w\times d h×w×d的3维array,其中 h h h和 w w w都是空间尺寸, d d d是特征维度或通道数。第一层是图像,尺寸为 h × w h\times w h×w,颜色通道数为 d d d。高维层中的位置对应回与其直接相关的图像的位置,叫做感受野(receptive fields)。
卷积网络是基于平移不变性建立的。其包含的基本元素(卷积、池化、激活函数)都是在局部输入区域上操作的,仅取决于相对空间坐标(relative spatial coordinates)。用 x i j \mathbf{x}_{ij} xij记录在某个特定层上位置 ( i , j ) (i,j) (i,j)处的数据向量,用 y i j \mathbf{y}_{ij} yij表示接下来的层的数据向量,则这些函数通过下式计算 y i j \mathbf{y}_{ij} yij:
y i j = f k s ( { x s i + δ i , s j + δ j } 0 ≤ δ i , δ j ≤ k ) \mathbf{y}_{ij}=f_{ks}(\{x_{si+\delta i,sj+\delta j}\}_{0\leq\delta i, \delta j\leq k}) yij=fks({xsi+δi,sj+δj}0≤δi,δj≤k)
其中 k k k成为和尺寸, s s s称为步长(stride)或subsampling factor, f k s f_{ks} fks决定了层的类型:用于卷积或平均池化的矩阵乘法,用于max pooling的求空间最大值,或用于激活函数的元素级非线性操作,以及用于其他类型层的操作。
这些函数形式在组合后也维持不变,且核尺寸和补偿遵循下面的规则:
f k s ∘ g k ′ s ′ = ( f ∘ g ) k ′ + ( k − 1 ) s ′ , s s ′ f_{ks}\circ g_{k's'}=(f\circ g)_{k'+(k-1)_{s',ss'}} fks∘gk′s′=(f∘g)k′+(k−1)s′,ss′
一个常规的深度网络计算常规非线性函数,而只有这种形式的层的网络计算了一个非线性filter,论文中称其为deep filter或fully convolutional network。一个FCN本质上可以计算任何尺寸的输入,且在正确resample条件下,可以输出与之空间尺寸对应的输出。
一个由FCN定义的实值损失函数(real-valued loss function)定义了一个task。如果损失函数是最后一层空间维度上求和, l ( x ; θ ) = ∑ i j l ′ ( x i j ; θ ) \mathscr l(\mathbf x;\theta)=\sum_{ij}l'(\mathbf x_{ij};\theta) l(x;θ)=∑ijl′(xij;θ),其梯度将是其每个空间成分的梯度之和。因此,整幅图像 l \mathcal l l上的随机梯度下降与 l ′ l' l′上的随机梯度下降相同,而将最后一层的所有感受野视为一个minibatch。
当这些感受野严重重叠时,无论是前向计算还是反向传播,在整张图像上的计算都比一个patch一个patch地计算要高效。
论文随后介绍了如何将分类网络转换成输出coarse output maps的fully convolutional nets。对于像素级估计,还需要将这些coarse outputs转换回像素。Section3.2介绍了一种实现这个功能的OverFeat。
Adapting classifiers for dense prediction
尽管LeNet和AlextNet等传统识别网络(recognition nets)表面上接受固定尺寸的输入并输出nonspatial outputs,它们所使用的全连接层却固定了维度并抛弃了空间坐标。尽管如此,这些全连接层也可以被视作是对整张图片进行的卷积。这样就将它们转换成了可以接收任意尺寸输入并生成输出分类map的全卷积网络。下图描述了这一变换。(相反地,诸如Le等人提出的nonconvolutional nets就缺少了这个能力)
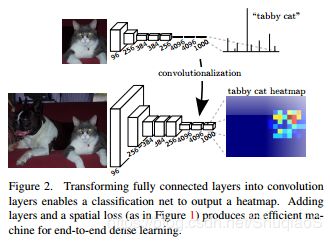
此外,尽管得到的maps对于特定的输入patches是相同的,但这些patch重叠部分的计算量却被高度降低了。比如,AlexNet在一个GPU上需要1.2ms来生成一幅227x227图像的分类score,全卷积版本则可以在22ms内生成500x500图像的10x10网格的输出,也就是大概比原来版本快了5倍。
这一空间输出map的特性使得这种模型非常适合解决诸如语义分割等dense problems。在前向通路速度差不多的情况下,对应的AlexNet需要2.4ms处理一张图片,而一个全卷积10x10输出map只需要37ms。下图显示了稠密反向传播的过程。
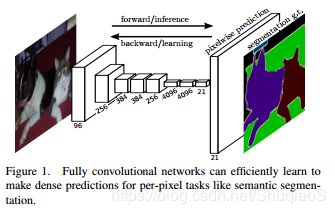
尽管将分类网络重新解释成全卷积网络能够在任意输入尺寸的情况下生成输出maps,但是由于过程中的下采样,输出通常会是输入尺寸的按比例缩小(与步长有关)。因为分类网络为了保证较小的滤波器和合理的计算量,通常会进行下采样。
Shift-and-stitch is filter rarefaction
OverFeat中介绍了通过输入平移和输出交错的方法,在不用插值的情况下,从coarse outputs生成稠密估计。如果输出按系数 f f f进行了下采样,则输入(通过左侧和上面的padding)向右平移 x x x个像素和向下平移 y y y个像素,每次平移的值 ( x , y ) ∈ { 0 , … , f − 1 } × { 0 , … , f − 1 } (x,y)\in\{0,\dots,f-1\}\times\{0,\dots,f-1\} (x,y)∈{0,…,f−1}×{0,…,f−1}。这 f 2 f^2 f2个输入每个都通过convnet,输出再交错在一起,从而保证每个像素点对应的估计都是位于其感受野的中心。
仅改变convnet的filter和layer strides也可以实现和shift-and-stitch相同的输出。假设有一个层(卷积或pooling),其输入步长为 s s s,随后的卷积层filter weights f i j f_{ij} fij(忽略特征维度,此处没有影响),如果将低层的输入步长设为1将其输出上采样 s s s倍的效果,与shift-and-stitch相同。然而,其输出却不同,因为原始filter只看到了其输入的一个部分。为了复现这种方法,将filter扩大为:
f i j ′ = { f i / s . j / s if s divides both i and j 0 otherwise f'_{ij}=\begin{cases} f_{i/s.j/s} & \text{if}\ s\ \text{divides both}\ i\ \text{and}\ j \\ 0 & \text{otherwise} \end{cases} fij′={fi/s.j/s0if s divides both i and jotherwise
其中 i i i和 j j j从0开始。
下面这一部分写了结果无法保存,不想重新写了,直接把原文放上来……真是*******
Upsampling is backwards strided convolution
Patchwise training is loss sampling
Segmentation Architecture

训练和交叉验证集用的是PASCAL VOC 2011分割挑战赛。训练用的损失是逐像素的多项式逻辑损失(per-pixel multinomial logistic loss);交叉验证用的是mean pixel intersection over union,其中均值来自于所有类别,包括背景。训练中忽略的像素被从真值中mask out(有歧义或者困难)。
From classifier to dense FCN
首先从已经证实的分类网络的卷积化开始。这里考虑的是赢得了ILSVRC12的AlexNet结构和在ILSVRC14中表现异常优异的VGG nets和GoogLeNet。这里选择的是VGG 16-layer net(在这项任务中与19-layer net表现相当)。对于GoogleNet,只用了最后的损失层,并通过丢弃最后的平均池化层实现了效果的提升。具体的修改方式是,将这些网络最后的分类层去掉,用卷积层替代所有的全连接层。具体地,用 1 × 1 1\times1 1×1的卷积(通道数21)来估计所有coarse output中在PASCAL上对应的每个类别(包括背景),再用deconvolution layer对coarse outputs进行双线性上采样实现像素级稠密估计。下表比较了每个网络的初级验证效果。这里显示的是固定学习率下收敛后的最优结果(至少175个epoch)。
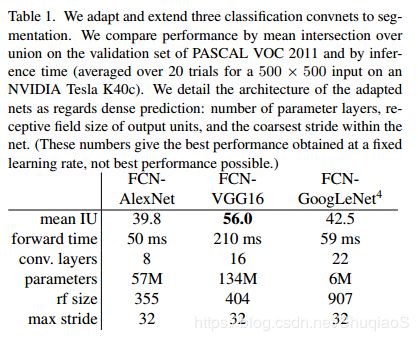
从分类到分割进行finetune在每个网络下都给出了合理的估计,即使是最差的网络结构也大概实现了约75%的state-of-the-art performance。用segmentation-equipped VGG net(FC-VGG16)已经以验证集上的平均IU 56.0实现了state-of-the-art表现(相比较于在测试集上的52.6)。用额外数据训练提升了在验证集上的表现到59.4。后续给出了具体的实验细节。
Combining what and where
(这一部分介绍的网络是本文中效果最好的网络。)
论文中定义了一个用于分割的全卷积网络(Fully convolutional net, FCN)将特征整合起来并优化了空间输出的精度。如下图所示。
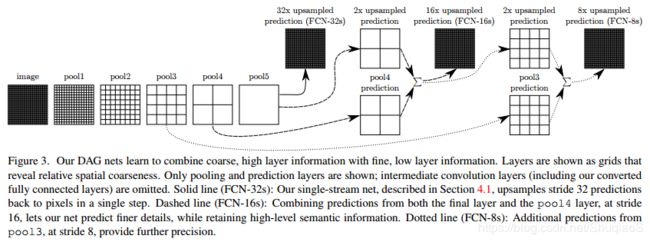
尽管全卷积分类器可以像前文说的直接finetune用于分割,效果也不错,但是其输出还是很粗糙,不令人满意的。如下图所示。32步长限制了最终上采样得到结果的细节吃醋。

论文作者通过加links的方法解决这个问题,也就是将最终的层与低级层相连。通过类比Florack等人的multiscale local jet,论文作者称这个非线性局部特征分层(nonlinear local feature hierarchy)为deep jet。
首先通过估计一个16像素步长的层将输出步长减半,在pool4层后面加一个1x1的卷积层以增加额外的类别估计。将这个输出与conv7(convolutionalized fc7)的结果融合,步长32,增加了2倍上采样层再对结果求和。(如上面Figure 3所示)。这个2倍上采样层初始化用的是双线性插值,但是里面的参数可以像前文说过的那样学习得到。最后,步长16的估计结果就这样得到了,随后上采样至图像尺寸。作者称之为FCN-16s。FCN-16s是端到端学习的,初始化由前面的FCN-32s的参数得到。应用在pool4上的参数是0初始化的,学习率下降比为100。
加上了skip net将验证集上的mean IU提升至62.4,如上面Figure 4所示。继续这个操作,效果提升至62.7。


Experimental framework
优化:
优化方法:带动量的SGD,动量0.9,weight decay 5 − 4 5^{-4} 5−4或 2 − 4 2^{-4} 2−4。
minibatch size:20张图片。
固定学习率:FCN-AlexNet( 1 0 − 3 10^{-3} 10−3)、FCN-VGG16( 1 0 − 4 10^{-4} 10−4)、FCN-GoogLeNet( 1 0 − 5 10^{-5} 10−5)。(学习率的确定通过line search)。对biases学习率翻倍。
初始化用的zero-initialze,因为作者发现随机初始化既没有提升表现,也没有加快速度。
Dropout仅在原来网络中使用的位置使用。
Fine-tuning:
整个网络中的所有层是一起反向传播的。仅通过Fine-tuning分类器的输出如Table 2所示,仅达到了总效果的70%。而考虑到训练时长,从最开始开始训练是不现实的。Fine-tuning在单个GPU上耗时三天以得到coarse FCN-32s,后续的FCN-16s和FCN-8s各耗费一天。
Patch Sampling
![]()

Class Balancing
全卷积训练可以通过权重或损失采样平衡类别。尽管论文中的标签都是midly unbalanced(约3/4是背景),但作者发现类别平衡也不是必要的。
Dense Prediction
scores通过网络内的deconvolution layers被上采样到图像维度。最终层的deconvolutional filters固定为双线性插值,而中间的以双线性插值初始化,随后学习更新。Shift-and-stitch或其他filter稀疏手段没有被使用。
Augmentation
作者尝试通过随机镜像和将图像各个维度jittering至最高32像素(相对于coarse scale of prediction)来扩张输入,但是这个操作没有带来明显提升。
More Training Data
Table 1中用到的PASCAL VOC 2011数据库标注了1112张图片。Hariharan等人收集了更大的8498张PASCAL训练图片(被用于训练之前的state-of-the-art system,比如SDS)。这个数据库将FCN-VGG16的mean IU提升至59.4(提高了3.4)。
Implementation
所有模型的训练和测试都是在Caffe上完成的,用的是单个NVIDIA Tesla K40c。模型和代码公开在这里。
Results
网络在PASCAL VOC,NYUDv2和SIFT Flow上进行了测试。
度量
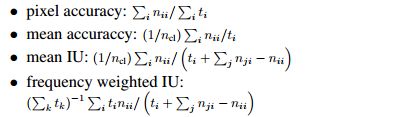
PASCAL VOC

NYUDv2
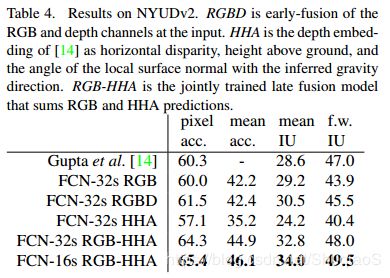
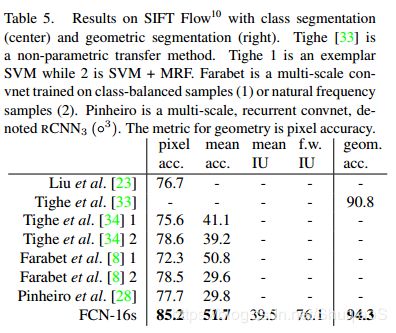
SIFT Flow