GMM与EM算法的Python实现

GMM与EM算法的Python实现

高斯混合模型(GMM)是一种常用的聚类模型，通常我们利用最大期望算法(EM)对高斯混合模型中的参数进行估计。

本教程中，我们自己动手一步步实现高斯混合模型。完整代码在第4节。

预计学习用时：30分钟。

本教程基于Python 3.6。

原创者：u_u | 修改校对：SofaSofa TeamM |

---

1. 高斯混合模型(Gaussian Mixture models, GMM)

高斯混合模型（Gaussian Mixture Model，GMM）是一种软聚类模型。
GMM也可以看作是K-means的推广，因为GMM不仅是考虑到了数据分布的均值，也考虑到了协方差。和K-means一样，我们需要提前确定簇的个数。

GMM的基本假设为数据是由几个不同的高斯分布的随机变量组合而成。如下图，我们就是用三个二维高斯分布生成的数据集。

在高斯混合模型中，我们需要估计每一个高斯分布的均值与方差。从最大似然估计的角度来说，给定某个有$n$个样本的数据集$X$，假如已知GMM中一共有$k$簇，我们就是要找到$k$组均值${\mu }_1,\cdots ,{\mu }_k$，$k$组方差${\sigma }_1,\cdots ,{\sigma }_k$来最大化以下似然函数$\mathcal{L}$
$$\mathcal{L}(({\mu }_1,\cdots ,{\mu }_k),({\sigma }_1,\cdots ,{\sigma }_k);X).$$

这里直接计算似然函数比较困难，于是我们引入隐变量(latent variable)，这里的隐变量就是每个样本属于每一簇的概率。假设$W$是一个$n\times k$的矩阵，其中$W_{i,j}$是第$i$个样本属于第$j$簇的概率。

在已知$W$的情况下，我们就很容易计算似然函数${\mathcal{L}}_W$，

$${\mathcal{L}}_W(({\mu }_1,\cdots ,{\mu }_k),({\sigma }_1,\cdots ,{\sigma }_k);X),$$
将其写成

$${\mathcal{L}}_W=\prod _{i=1}^n\left(\sum _{j=1}^k{W}_{i,j}P(X_i|{\mu }_j,{\sigma }_j)\right)$$

其中$P(X_i|{\mu }_j,{\sigma }_j)$是样本$X_i$在第$j$个高斯分布中的概率密度函数。

以一维高斯分布为例，
$$P(X_i|{\mu }_j,{\sigma }_j)=\frac{1}{\sqrt{2\pi {\sigma }_j^2}}{e}^{-\frac{(X_i-{\mu }_j{)}^2}{2{\sigma }_j^2}}$$

2. 最大期望算法(Expectation–Maximization, EM)

有了隐变量还不够，我们还需要一个算法来找到最佳的$W$，从而得到GMM的模型参数。EM算法就是这样一个算法。

简单说来，EM算法分两个步骤。

• 第一个步骤是E（期望），用来更新隐变量$W$；
• 第二个步骤是M（最大化），用来更新GMM中各高斯分布的参量${\mu }_j$, ${\sigma }_j$。

然后重复进行以上两个步骤，直到达到迭代终止条件。

3. 具体步骤以及Python实现

完整代码在第4节。

首先，我们先引用一些我们需要用到的库和函数。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from scipy.stats import multivariate_normal
plt.style.use('seaborn')

接下来，我们生成2000条二维模拟数据，其中400个样本来自$\mathcal{N}({\mu }_1,{\text{var}}_1)$，600个来自$\mathcal{N}({\mu }_2,{\text{var}}_2)$，1000个样本来自$\mathcal{N}({\mu }_3,{\text{var}}_3)$

# 第一簇的数据
num1, mu1, var1 = 400, [0.5, 0.5], [1, 3]
X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1)
# 第二簇的数据
num2, mu2, var2 = 600, [5.5, 2.5], [2, 2]
X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2)
# 第三簇的数据
num3, mu3, var3 = 1000, [1, 7], [6, 2]
X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3)
# 合并在一起
X = np.vstack((X1, X2, X3))

数据如下图所示：

plt.figure(figsize=(10, 8))
plt.axis([-10, 15, -5, 15])
plt.scatter(X1[:, 0], X1[:, 1], s=5)
plt.scatter(X2[:, 0], X2[:, 1], s=5)
plt.scatter(X3[:, 0], X3[:, 1], s=5)
plt.show()

3.1 变量初始化

首先要对GMM模型参数以及隐变量进行初始化。通常可以用一些固定的值或者随机值。

n_clusters是GMM模型中聚类的个数，和K-Means一样我们需要提前确定。这里通过观察可以看出是3。（拓展阅读：如何确定GMM中聚类的个数？）

n_points是样本点的个数。

Mu是每个高斯分布的均值。

Var是每个高斯分布的方差，为了过程简便，我们这里假设协方差矩阵都是对角阵。

W是上面提到的隐变量，也就是每个样本属于每一簇的概率，在初始时，我们可以认为每个样本属于某一簇的概率都是$1/3$。

Pi是每一簇的比重，可以根据W求得，在初始时，Pi = [1/3, 1/3, 1/3]

n_clusters = 3
n_points = len(X)
Mu = [[0, -1], [6, 0], [0, 9]]
Var = [[1, 1], [1, 1], [1, 1]]
Pi = [1 / n_clusters] * 3
W = np.ones((n_points, n_clusters)) / n_clusters 
Pi = W.sum(axis=0) / W.sum()

3.2 E步骤

E步骤中，我们的主要目的是更新W。第$i$个变量属于第$m$簇的概率为：

$$W_{i,m}=\frac{{\pi }_{j}P(X_i|{\mu }_m,{\text{var}}_m)}{{\sum }_{j=1}^3{\pi }_{j}P(X_i|{\mu }_j,{\text{var}}_j)}$$

根据$W$，我们就可以更新每一簇的占比${\pi }_m$，

$${\pi }_m=\frac{{\sum }_{i=1}^n{W}_{i,m}}{{\sum }_{j=1}^k{\sum }_{i=1}^n{W}_{i,j}}$$

def update_W(X, Mu, Var, Pi):
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    W = pdfs / pdfs.sum(axis=1).reshape(-1, 1)
    return W


def update_Pi(W):
    Pi = W.sum(axis=0) / W.sum()
    return Pi

以下是计算对数似然函数的logLH以及用来可视化数据的plot_clusters。

def logLH(X, Pi, Mu, Var):
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    return np.mean(np.log(pdfs.sum(axis=1)))


def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None):
    colors = ['b', 'g', 'r']
    n_clusters = len(Mu)
    plt.figure(figsize=(10, 8))
    plt.axis([-10, 15, -5, 15])
    plt.scatter(X[:, 0], X[:, 1], s=5)
    ax = plt.gca()
    for i in range(n_clusters):
        plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'ls': ':'}
        ellipse = Ellipse(Mu[i], 3 * Var[i][0], 3 * Var[i][1], **plot_args)
        ax.add_patch(ellipse)
    if (Mu_true is not None) & (Var_true is not None):
        for i in range(n_clusters):
            plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'alpha': 0.5}
            ellipse = Ellipse(Mu_true[i], 3 * Var_true[i][0], 3 * Var_true[i][1], **plot_args)
            ax.add_patch(ellipse)         
    plt.show()

3.2 M步骤

M步骤中，我们需要根据上面一步得到的W来更新均值Mu和方差Var。
Mu和Var是以W的权重的样本X的均值和方差。

因为这里的数据是二维的，第$m$簇的第$k$个分量的均值，

$$\mu \_m,k=\frac{\sum \_{i=1}^{n}W\_i,mX\_i,k}{\sum \_{i=1}^{n}W\_i,m}$$

第$m$簇的第$k$个分量的方差，

$${\text{var}}_{m,k}=\frac{{\sum }_{i=1}^n{W}_{i,m}(X_{i,k}-{\mu }_{m,k}{)}^2}{{\sum }_{i=1}^n{W}_{i,m}}$$
以上迭代公式写成如下函数update_Mu和update_Var。

def update_Mu(X, W):
    n_clusters = W.shape[1]
    Mu = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Mu[i] = np.average(X, axis=0, weights=W[:, i])
    return Mu

def update_Var(X, Mu, W):
    n_clusters = W.shape[1]
    Var = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Var[i] = np.average((X - Mu[i]) ** 2, axis=0, weights=W[:, i])
    return Var

3.3 迭代求解

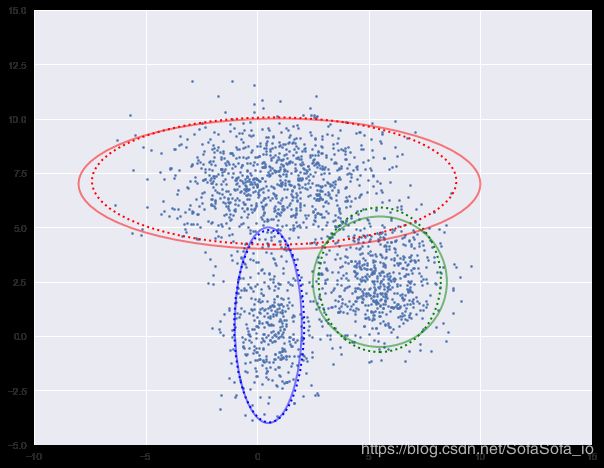
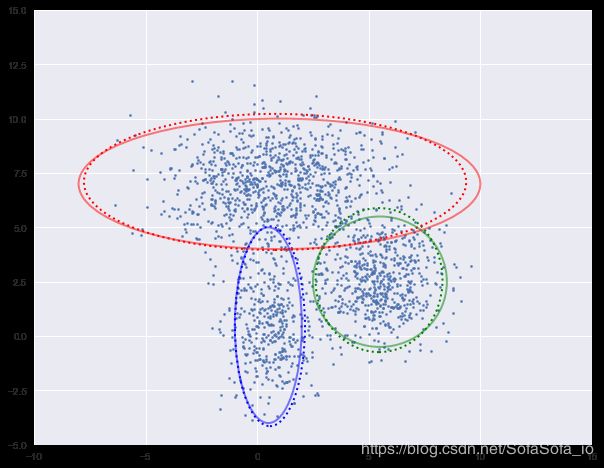
下面我们进行迭代求解。

图中实现是真实的高斯分布，虚线是我们估计出的高斯分布。可以看出，经过5次迭代之后，两者几乎完全重合。

loglh = []
for i in range(5):
    plot_clusters(X, Mu, Var, [mu1, mu2, mu3], [var1, var2, var3])
    loglh.append(logLH(X, Pi, Mu, Var))
    W = update_W(X, Mu, Var, Pi)
    Pi = update_Pi(W)
    Mu = update_Mu(X, W)
    print('log-likehood:%.3f'%loglh[-1])
    Var = update_Var(X, Mu, W)

log-likehood:-8.054

log-likehood:-4.731

log-likehood:-4.729

log-likehood:-4.728

log-likehood:-4.728

4. 完整代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from scipy.stats import multivariate_normal
plt.style.use('seaborn')

# 生成数据
def generate_X(true_Mu, true_Var):
    # 第一簇的数据
    num1, mu1, var1 = 400, true_Mu[0], true_Var[0]
    X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1)
    # 第二簇的数据
    num2, mu2, var2 = 600, true_Mu[1], true_Var[1]
    X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2)
    # 第三簇的数据
    num3, mu3, var3 = 1000, true_Mu[2], true_Var[2]
    X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3)
    # 合并在一起
    X = np.vstack((X1, X2, X3))
    # 显示数据
    plt.figure(figsize=(10, 8))
    plt.axis([-10, 15, -5, 15])
    plt.scatter(X1[:, 0], X1[:, 1], s=5)
    plt.scatter(X2[:, 0], X2[:, 1], s=5)
    plt.scatter(X3[:, 0], X3[:, 1], s=5)
    plt.show()
    return X


# 更新W
def update_W(X, Mu, Var, Pi):
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    W = pdfs / pdfs.sum(axis=1).reshape(-1, 1)
    return W


# 更新pi
def update_Pi(W):
    Pi = W.sum(axis=0) / W.sum()
    return Pi


# 计算log似然函数
def logLH(X, Pi, Mu, Var):
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    return np.mean(np.log(pdfs.sum(axis=1)))


# 画出聚类图像
def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None):
    colors = ['b', 'g', 'r']
    n_clusters = len(Mu)
    plt.figure(figsize=(10, 8))
    plt.axis([-10, 15, -5, 15])
    plt.scatter(X[:, 0], X[:, 1], s=5)
    ax = plt.gca()
    for i in range(n_clusters):
        plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'ls': ':'}
        ellipse = Ellipse(Mu[i], 3 * Var[i][0], 3 * Var[i][1], **plot_args)
        ax.add_patch(ellipse)
    if (Mu_true is not None) & (Var_true is not None):
        for i in range(n_clusters):
            plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'alpha': 0.5}
            ellipse = Ellipse(Mu_true[i], 3 * Var_true[i][0], 3 * Var_true[i][1], **plot_args)
            ax.add_patch(ellipse)         
    plt.show()
    

# 更新Mu
def update_Mu(X, W):
    n_clusters = W.shape[1]
    Mu = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Mu[i] = np.average(X, axis=0, weights=W[:, i])
    return Mu


# 更新Var
def update_Var(X, Mu, W):
    n_clusters = W.shape[1]
    Var = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Var[i] = np.average((X - Mu[i]) ** 2, axis=0, weights=W[:, i])
    return Var


if __name__ == '__main__':
    # 生成数据
    true_Mu = [[0.5, 0.5], [5.5, 2.5], [1, 7]]
    true_Var = [[1, 3], [2, 2], [6, 2]]
    X = generate_X(true_Mu, true_Var)
    # 初始化
    n_clusters = 3
    n_points = len(X)
    Mu = [[0, -1], [6, 0], [0, 9]]
    Var = [[1, 1], [1, 1], [1, 1]]
    Pi = [1 / n_clusters] * 3
    W = np.ones((n_points, n_clusters)) / n_clusters 
    Pi = W.sum(axis=0) / W.sum()
    # 迭代
    loglh = []
    for i in range(5):
        plot_clusters(X, Mu, Var, true_Mu, true_Var)
        loglh.append(logLH(X, Pi, Mu, Var))
        W = update_W(X, Mu, Var, Pi)
        Pi = update_Pi(W)
        Mu = update_Mu(X, W)
        print('log-likehood:%.3f'%loglh[-1])
        Var = update_Var(X, Mu, W)

出处：SofaSofa机器学习社区

---

机器学习、数据科学面经、面试题