概率图系列之隐马尔可夫模型（HMM）

概率图模型

概率图模型是一类用图来表达变量相关关系的概率模型。常见的是用一个节点表示一个或一组随机变量，节点之间的边表示变量之间的概率相关关系，如下图：

概率图根据边的性质，可以划分为两种：

• 有向图无环图——有向图模型或贝叶斯网
• 无向图——无向图图或马尔可夫网

隐马尔可夫模型（HMM）

性质：结构最简单的动态贝叶斯网——有向无环图
描述：由一个隐藏的马尔可夫链生成不可观测的状态随机序列，再由各个状态生成一个可观测而产生观测随机序列的过程。

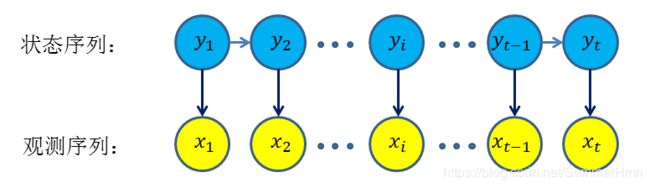
上图的箭头表示依赖关系，HMM做了两个基本假设：

• 齐次马尔可夫假设：隐藏的马尔可夫链在任一时刻$t$的状态只依赖于上一个时刻$t-1$的状态
  $$p(y_t|y_1,x_1,y_2,x_2...,y_{t-1},x_{t-1})=p(y_t|y_{t-1})$$
• 观测独立性假设：任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测即状态无关
  $$p(x_t|y_1,x_1,y_2,x_2...,y_{t-1},x_{t-1},y_t)=p(x_t|y_t)$$
  

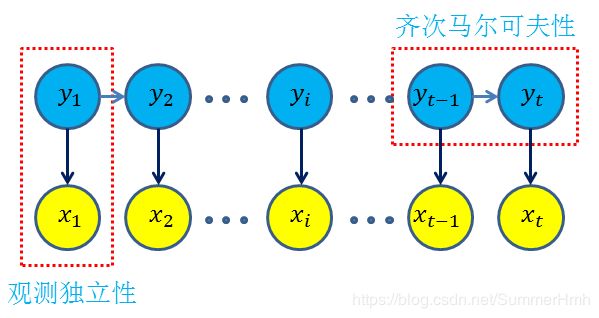
基于如上的两个假设，可以获取所有变量的联合概率分布为：
$$p(x_1,y_1,x_2,y_2,...,x_t,y_t)=p(y_1)p(x_1|y_1)\prod _{i=2}^{t}p(y_i|y_{i-1})p(x_i|y_i)$$
其中$y\in \{s_1,s_2,...,s_N\}$，表示有N种状态，$x\in \{o_1,o_2,...,o_M\}$，表示有M种观测值。
除了结构信息，根据联合概率分布可得，如果要确定一个HMM，需要以下三组参数：

• 初始状态概率：模型在初始时刻各状态出现的概率，即$p(y)$，通常记为$\pi =({\pi }_1,{\pi }_2,...,{\pi }_N)$，$N$为状态的种类，其中
  $${\pi }_i=p(y=s_i),1⩽i⩽N$$
• 状态转移概率：模型在各个状态间转换的概率，通常记为$\mathbf{A}=[a_{ij}{]}_{N\times M}$
  $$a_{ij}=p(y_{t+1}=s_j|y_t=s_i)$$
• 输出观测概率：模型根据当前状态获得各个观测值得概率，通常记为$\mathbf{B}=[b_{ij}{]}_{N\times M}$，状态$s_i$下观测值为$o_j$的概率
  $$b_{ij}=p(x_t=o_j|y_t=s_i)$$

这样，一个HMM模型可以表示为$\lambda =[\mathbf{A},\mathbf{B},\pi ]$

观测序列的生成

已知HMM的模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，可根据模型生成观测序列

• 步骤
  输入：HMM模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，观测序列长度$T$
  输出：观测序列$\mathbf{x}=(x_1,x_2,...,x_T)$
  （1）设置$t=1$，并根据初始状态概率$\pi$产生状态$y_1$
  （2）按照状态$y_t$的观测输出概率$\mathbf{B}$输出观测序列$x_t$
  （3）根据状态转移概率$\mathbf{A}$和$y_t$产生状态$y_{t+1}$
  （4）$t=t+1$，跳转到第（2）步，如果$t=T$，结束输出

• 代码
  初始状态，和观测状态都是属于多项分布，因此通过多项分布进行模拟

import numpy as np
np.random.seed(1234) # 设置随机种子，使得可以复现
#numpy.random.multinomial(n, pvals, size=None) n : int：实验次数 pvals：浮点数序列，长度p,P个不同结果的概率,值和为1 size : 输出形状,每次为一个迭代
#测试np.random.multinomial效果
np.random.multinomial(5, [0.3,0.7], size=1)
np.random.multinomial(5, [0.3,0.7], size=2)
#生成序列代码

class HMM():
    def __init__(self,A,B,pi,N=0,M=0):
        self.A=A
        self.B=B
        self.pi=pi
        if N==0 :
            self.N=len(self.A)
        else:
            self.N=N
        if M==0:
            self.M=len(self.B[0])
        else:
            self.M=M
    
    # 模拟序列
    def simulate(self,T):
        def genetate_from(probs):
            return np.where(np.random.multinomial(1,probs)==1)[0][0]
        obs=np.zeros(T,dtype=int)
        states=np.zeros(T,dtype=int)
        states[0]=genetate_from(self.pi)
        obs[0]=genetate_from(self.B[states[0],:])
        for t in range(1,T):
            states[t]=genetate_from(self.A[states[t-1],:])
            obs[t]=genetate_from(self.B[states[t],:])
        return states,obs

#模型参数
A=np.array([[0,1,0,0],[0.4,0,0.6,0],[0,0.4,0,0.6],[0,0,0.5,0.5]])
B=np.array([[0.5,0.5],[0.3,0.7],[0.6,0.4],[0.8,0.2]])
pi=np.array([0.25]*4)
states_bag=["box1","box2","box3","box4"]
obs_bag=["red","white"]

#进行模拟输出
hmm=HMM(A,B,pi)
states,obs=hmm.simulate(10)

print("状态序列：",end="  ")
for i in states:
    print("{:6s}".format(states_bag[i]),end=" ")
print()
print("观测序列：",end="  ")
for i in obs:
    print("{:6s}".format(obs_bag[i]),end=" ")

结果：

HMM的三个基本问题及解法

HMM主要有三个应用点

• 概率问题：已知观测序列$\mathbf{x}$和模型$\lambda$，计算在模型$\lambda$下，观测序列$\mathbf{x}$出现的概率$p(\mathbf{x}|\lambda )$
• 学习问题：已知观测序列$\mathbf{x}$，估计模型的参数$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，使得该模型下观测序列概率$p(\mathbf{x}|\lambda )$最大，可用MLE
• 预测问题：已知观测序列$\mathbf{x}$和模型$\lambda$，求最有可能的对应状态序列

概率问题

直接计算

列举长度为$T$所有可能的状态序列$\mathbf{y}$，一共有$N^T$种，然后求各个状态对应观测序列的联合概率$p(\mathbf{x},\mathbf{y}|\lambda )$，再对所有可能的状态序列求和，得到$p(\mathbf{x}|\lambda )$
$$p(\mathbf{x},\mathbf{y}|\lambda )=p(\mathbf{x}|\mathbf{y},\lambda )p(\mathbf{y}|\lambda )$$
上式计算量很大，是$O(T{N}^T)$，一般不直接计算。

前向算法

前向概率：给定HMM的模型$\lambda$，定义到时刻$t$部分观测序列为$o_1,o_2,...,o_t$，且状态为$s_i$的概率为前向概率，记作
$${\alpha }_t(i)=p(o_1,o_2,...,o_t,y_t=s_i|\lambda )$$

• 算法步骤
  输入：HMM模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，观测序列$\mathbf{x}=(x_1,x_2,...,x_T)$
  输出：观测序列概率$p(\mathbf{x}|\lambda )$
  （1）初始化，根据初始概率，计算状态为$s_i$，观测结果为$o_1$的概率
  $${\alpha }_1(i)={\pi }_i{b}_i(o_1)$$
  （2）递推，对$t=1,2,...,T-1$
  $${\alpha }_t(i)=\left[\sum _{j=1}^N{\alpha }_t(j)a_{ji}\right]b_i(o_{t+1}),i=1,2,...,N$$
  （3）终止
  $$p(\mathbf{x}|\lambda )=\sum _{i=1}^N{\alpha }_T(i)$$

• 代码实现

    #前向算法
    def probsForward(self,x):
        T=len(x)
        alpha=np.zeros([T,self.N],dtype=float)
        for t in range(T):
            obt=int(x[t])
            if t==0 :
                alpha[t]=self.pi*self.B[:,obt]
            else:
                alpha[t]=np.multiply(np.sum(alpha[t-1]*self.A.T,axis=1),self.B[:,obt])
            #print(alpha[t])
        return np.sum(alpha[T-1]),alpha

时间复杂度 $O(N^{2}T)$，从时间方向，进行如下计算

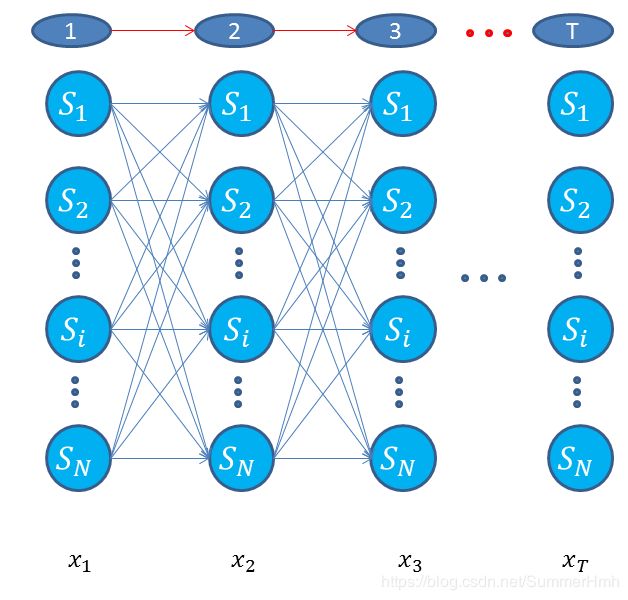
从时间切片，进行如下计算当前序列值为$o_j$的概率

后向算法

后向概率：给定HMM的模型$\lambda$，定义在$t$时刻状态为$s_i$的条件下，从$t+1$到T的部分观测序列$o_{t+1},o_{t+2},...,o_T,$$的概率为后验概率，记作
$${\beta }_t(i)=p(o_{t+1},o_{t+2},...,o_T|y_t=s_i,\lambda )$$

• 算法步骤
  输入：HMM模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，观测序列$\mathbf{x}=(x_1,x_2,...,x_T)$
  输出：观测序列概率$p(\mathbf{x}|\lambda )$
  （1）终值
  $${\beta }_T(i)=1,i=1,2,..,N$$
  （2）对于$t=T-1,T-2,...,1$
  $${\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)$$
  （3）结束
  $$p(\mathbf{x}|\lambda )=\sum _{i=1}^N{\pi }_i{b}_i(o_1){\beta }_1(i)$$

• 代码实现

    #后向算法
    def probsBack(self,x):
        T=len(x)
        beta=np.zeros([T,self.N],dtype=float)
        for t in range(T-1,-1,-1):
            if t==T-1:
                beta[t]=[1]*self.N
            else:
                beta[t]=np.sum(self.A*self.B[:,int(x[t+1])]*beta[t+1],axis=1)
        return np.sum(self.pi*self.B[:,int(x[0])]*beta[0]),beta

后向算法本质上跟前向算法一致，不过递推方向相反

概率和期望

• 给定模型$\lambda$和观测$\mathbf{x}$，在$t$时刻处于状态$s_i$的概率
  $${\gamma }_t(i)=p(i_t=s_i|\lambda ,\mathbf{x})=\frac{p(i_t=s_i,\mathbf{x}|\lambda )}{p(\mathbf{x}|\lambda )}$$$$\because {\alpha }_t(i){\beta }_t(i)=p(i_t=s_t,\mathbf{x}|\lambda )$$$$\therefore {\gamma }_t(i)=\frac{{\alpha }_t(i){\beta }_t(i)}{p(\mathbf{x}|\lambda )}=\frac{{\alpha }_t(i){\beta }_t(i)}{{\sum }_{j=1}^N{\alpha }_t(j){\beta }_t(j)}$$

• 给定模型$\lambda$和观测$\mathbf{x}$，在$t$时刻处于状态$s_i$，$t+1$时刻处于状态$s_j$的概率
  $${\xi }_t(i,j)=p(i_t=s_i,i_{t+1}=s_j|\lambda ,\mathbf{x})=\frac{p(i_t=s_i,i_{t+1}=s_j,\mathbf{x}|\lambda )}{p(\mathbf{x}|\lambda )}$$
  $$\because p(i_t=s_i,i_{t+1}=s_j,\mathbf{x}|\lambda )={\alpha }_t(s_i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)$$
  $$\therefore {\xi }_t(i,j)=\frac{{\alpha }_t(s_i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}{{\sum }_{j=1}^N{\sum }_{i=1}^N{\alpha }_t(s_i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}$$

• 在观测$\mathbf{x}$下状态$s_i$出现的期望值
  $$\sum _{t=1}^T{\gamma }_t(i)$$

• 在观测$\mathbf{x}$下由状态$s_i$转移的期望值
  $$\sum _{t=1}^{T-1}{\gamma }_t(i)$$

• 在观测$\mathbf{x}$下由状态$s_i$转移到状态$s_j$的期望值
  $$\sum _{t=1}^{T-1}{\xi }_t(i,j)$$

学习问题

根据观测序列学习HMM的模型的过程

监督学习

• 条件：已知观测序列和对应的状态序列
• 方法：频率统计
• 不足：需要人工标注数据

Baum-Welch 算法

• 模型
  $$p(\mathbf{x}|\lambda )=\sum _{y}p(\mathbf{x}|\mathbf{y},\lambda )p(\mathbf{y}|\lambda )$$
• 方法：EM算法和拉格朗日乘子法
• 参数估计公式
  $$a_{ij}=\frac{{\sum }_{t=1}^{T-1}{\xi }_t(i,j)}{{\sum }_{t=1}^{T-1}{\gamma }_t(i)}$$$$b_j(k)=\frac{{\sum }_{t=1o_t=v_k}^T{\gamma }_t(j)}{{\sum }_{t=1}^T{\gamma }_t(j)}$$$${\pi }_i={\gamma }_1(i)$$
  -步骤
  输入：观测数据$\mathbf{x}$
  输出：HMM的模型参数
  （1）初始化模型参数
  （2）递推，根据参数估计公式
  （3）终止，得到模型参数
• 代码实现

    def computeGammaAndXi(self,x):
        _,alpha=self.probsForward(x)
        _,beta=self.probsBack(x)
        T=len(x)
        gamma=np.zeros([T,self.N],dtype=float)
        xi=np.zeros([T-1,self.N,self.N],dtype=float)
        
        for t in range(T):
            gamma[t]=np.multiply(alpha[t],beta[t])/np.sum(np.multiply(alpha[t],beta[t]))
            if t < T-1:
                tmp=np.sum(np.dot(alpha[t],self.A)*self.B[:,int(x[t])]*beta[t+1])              
#                 for i in range(self.N):
#                         xi[t][i,:]=alpha[t][i]*self.A[i,:]*self.B[:,int(x[t+1])]*beta[t+1]/tmp     
                xi[t]=alpha[t]*self.A*self.B[:,int(x[t+1])]*beta[t+1]/tmp 
        return gamma,xi
                           
    #baum-Welch算法
    def baumWelch(self,x,e=0.0005):
        T=len(x)
       
        # 初始化模型参数 不能这样初始化——随机初始化，同时满足约束条件——待添加，目前默认上一次计算的结果值
#         self.A=np.ones([self.N,self.N],dtype=float)*1/self.N
#         self.B=np.ones([self.N,self.M],dtype=float)*1/self.M
#         self.pi=np.ones(self.N,dtype=float)*1/self.N
                
        while True:
            # E步
            gamma,xi=self.computeGammaAndXi(x)
            #M步
            newPi=gamma[0]
            newA=np.sum(xi,axis=0)/np.sum(gamma[:-1,:],axis=0)
            newB=np.copy(self.B)
            b_denominator=np.sum(gamma,axis=0)
            for k in range(self.M):
                temp_matrix=np.zeros((T,1))
                for t in range(T):
                    if int(x[t])==k:
                        temp_matrix[t][0]=1
                #print(gamma*temp_matrix)
                newB[:,k]=np.sum(gamma*temp_matrix,axis=0)/b_denominator
            
            # 更新参数
            self.A=newA
            self.B=newB
            self.pi=newPi     
            
            #终止阀值
            if np.max(abs(self.pi-newPi))

预测问题

根据观测序列和模型，求最可能的状态序列

近似算法

最大化$t$时刻状态为$s_i$的概率
$${\gamma }_t(i)=\frac{{\alpha }_t(i){\beta }_t(i)}{p(\mathbf{x}|\lambda )}=\frac{{\alpha }_t(i){\beta }_t(i)}{{\sum }_{j=1}^N{\alpha }_t(j){\beta }_t(j)}$$
得到的状态序列为最可能的状态序列
这种方法计算简单，但是不能保证预测的状态序列整体是最有可能的状态序列，存在实际不发生的转移情况。

维特比算法（Viterbi）

用动态规划求概率最大路径。如果最优路径在时刻$t$时刻状态为$s_i$，那么这一路径从节点$i_t$到终点$i_T$的部分路径，必须是最优路径。

• 算法
  在时刻$t$上状态为$s_i$的所有单个路径中概率最大值为：
  $${\delta }_t(i)=\max p(y_t=s_i,y_{t-1},....,y_1,o_t,...,o_1|\lambda )$$
  则
  $${\delta }_{t+1}(i)=\underset{1⩽j⩽N}{\max }\left[{\delta }_t(j)a_{ji}\right]b_i(o_{t+1})$$
  记录每条路线经过的节点，最后的一个时刻，最大概率的路径为最优路径。

• 算法思路
  （1）计算$t$时刻，状态为$s_i$的最大概率
  （2）根据$t$时刻的$s_i$最大概率，计算$t+1$时刻，状态为$s_j$的最大概率

• 代码实现

    # viterbi算法
    def viterbi(self,x):
        T=len(x)
        v=[{}]
        path={}
        for i in range(self.N):
            print(self.pi[i])
            v[0][i]=self.pi[i]*self.B[i][int(x[0])]
            path[i]=[i]
        
        for t in range(1,T):
            v.append({})
            newpath={}
            for i in range(self.N):
                prob,state=max([(v[t-1][j]*self.A[j][i]*self.B[i][int(x[t])],j) for j in range(self.N)])
                v[t][i]=prob
                newpath[i]=path[state]+[i]
            path=newpath
        prob,state=max([(v[T-1][i],i) for i in range(self.N)])
        print(path)
        return prob,path[state]

结语

之前对于HMM感觉一知半解，很多东西没有深入，看到HMM用于词性标注，深感自己知识的不通透，故此，整理一遍。

参考：李航《统计学习方法》
周志华 《机器学习》