关于卷积操作(Convolution)的理解(参数量和运算量计算),以及网络轻量化(MobileNet Inspired Depthwise Separable Conv深度可分离卷积)
深度学习,尤其是深度卷积网络的迅猛发展,使得其在存储和算力奢侈的GPU(多GPU)上的部属趋于成熟。然而,将基于深度CNN的方法有效移植到存储和算力有限的移动设备端(手机、Pad、嵌入式设备等)面临诸多挑战。
核心挑战就是如何降低CNN对memory(存储)和FLOPS(算力)的要求,但又保持CNN的性能(相比于其在GPU端的原貌)没有显著衰减。为解决这一核心挑战,我们就需要研究网络轻量化,具体说就是通过设计新的网络结构(archeticture)以及网络中不淑的卷积操作(Conv Ops),以实现 1. 减少网络参数量;2. 降低网络运算过程中的FLOPs。
关于轻量化网络的设计,八仙过海。这里希望和大家分享我对Google开发的MobileNet(V1-V3)系列网络的宏观感受。个人水平有限,也没有深入实现过MobileNet的各个版本,因此此处仅站在广义CNN设计的角度汇报一下。
MobileNet的杀手锏,是深度可分离卷积(Depthwise Separable Convolution)
For breviety,此博客把Depthwise Separable Conv简称为DSC。
要理解DSC,我们先回溯普通卷积。
------------------------------------------------------------------------Here We Go--------------------------------------------------------------------------------
I. 普通卷积是如何操作的?普通卷积所产生的参数量和FLOPs如何计算?
为粗糙的画功向大家致歉。。。赶论文比较急,没时间作图了。、
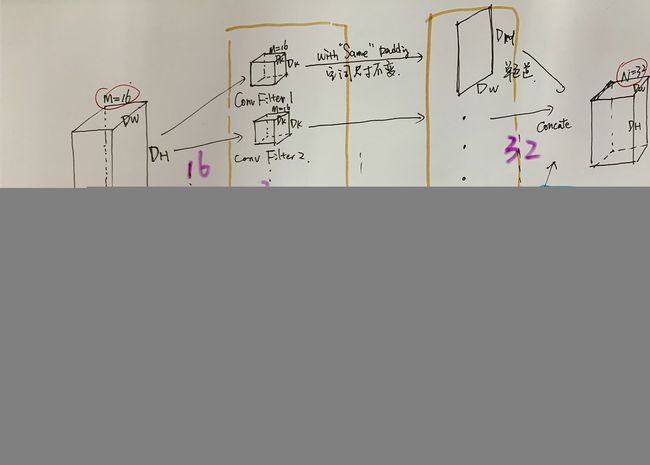
Convolution的本质是feature localization,即,在input feature map上将某些local、局部的feature通过滑窗计算cross-correlation相似度的方式(注:cross-correlation和卷积实质上是把filter旋转180度的关系),进行定位。该定位响应图,就是某个feature的卷积输出通道图。
普通卷积,概述就是一个filter一次性完整地卷input feature map的所有通道,所以filter本身是由channel dimension的。而每一个filter在卷完之后的输出是单通道的,所以该卷积层最后的输出有多少通道,就需要在该卷积层设置多少个不同的filter(但没一个fitler同样尺寸和channel)。
1. 一个Conv操作所涉及的参数量是:
(Dk * Dk * M) * N-------每个卷积核参数 * N个核
Dk是卷积核尺寸(3、5、7等),M是输入特征通道数,N是输出特征通道数。
可见,一个CNN网络architecture在设计时,如果有效控各个conv layer的制特征图channel数,以及卷积和空间大小,则有可能控制该CNN的整体参数量。卷积核尺寸越小、channel越浅,参数越少。
2. 一个Conv操作所涉及的计算量(所需算力)是:
(Dk * Dk * M * N)* Dw * DH
括号中是一个Conv的参数量。Conv在执行的时候是elementwise multiplciaiton then summation。所以一个Conv filter进行一次操作(即对input滑窗一遍)的计算量就是:
每个滑窗位置产生的计算量 * 滑窗位置的个数
由于是elementwise multiplicaiton + summation,所以每个滑窗位置产生的计算量 = 每个卷积核的参数量
所以一个卷积层操作的计算量等于其所有卷积核的参数量 * 输入图尺寸(假设SAME padding)。
如果选用SAME pading保持卷积输入输出空间尺寸不变,那么滑窗位置的个数就等于输入空间尺寸(可以理解为,输出图上每个pixel的数值是conv filter在对应位置上进行cross-correlation计算所得的scalar数值)。
由此可见,卷积的计算量不仅与卷积核本身的尺寸、网络中特征图channel数相关,还与网络中特征图的空间尺寸相关。
所以,若输入图片大小固定,那么CNN中conv层设计使得网络中特征图尺寸越小(早、多pooling进行降采)+ 保持特征图通道数较小,则整个CNN的memeory和FLOPs较小。
但是,这明显是约束该网络的空间精细度(spatail fidelity)和语义深度(semantic depth)。好大的treade-off!
II. Spatialwise Separable Conv和DSC都可以对普通Conv实现轻量化。
Spatialwise Separable Conv就是将一个 空间大小3 * 3的filter拆解成先卷一个3 * 1 再卷一个1 * 3.
3 * 3 = 9, 3 * 1 + 1 * 3 = 6, 9 > 6
III. DSC
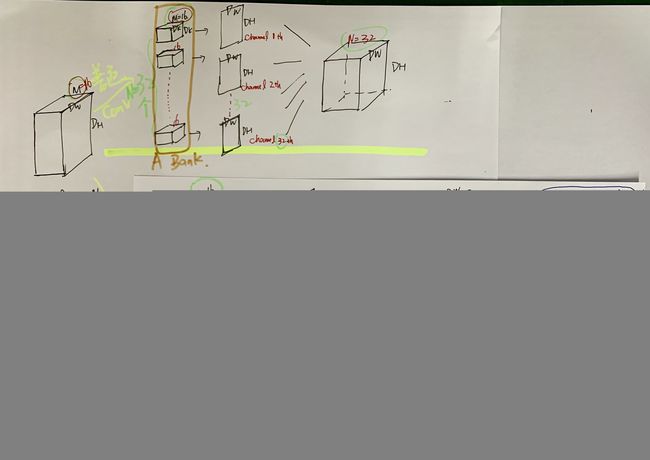
DSC是将一个普通卷积拆解为先depthwise convolution(逐个通道单独做输入输出均为1 channel的卷积),再做pointwise convolution(通道数目调控)。
1. Depthwise conv的意义是将输入feature map拆解为各个单个通道,并在各个通道上做输入输出均为1通道的卷积,所以一个DSC的depthwsie conv阶段涉及到的参数为:
(Dk * Dk) * M
括号中是每个单个通道上的filter的参数,M是M个通道。
2. pointwise conv是用1 * 1 conv filter将M输入通道扩张到N输出通道(Channel Manipulation)。
(1 * 1 * M) * N
括号中是用1 * 1 大小filter一齐卷M个channel的depthwise conv输出,N是有N个这样的1 * 1 * M个filters。
3. 一个DSC卷积层和一个普通Conv层总参数比较:Dk=3, M = 16, N = 32
DSC:Dk * Dk * M + 1 * 1 * M * N = 656
普通Conv:Dk * Dk * M * N = 4608