PCA降维方法及在AT&T人脸数据集的应用实例

本篇博文对AT&T剑桥大学实验室[1]的人脸数据集应用了主成分分析策略, 做了一些可视化处理.

算法原理

---

假设在 Rn R n 空间中有 m m 个点, 我们希望对这些点进行有损压缩, 使数据的维度从 Rn R n 变为 Rl R l , 其中严格的有 l<n l < n .
这时候主成分分析法(PCA)便可以实现我们的要求.
对于每个点 xi∈Rn x i ∈ R n , 使得其被投影为 ci∈Rl c i ∈ R l , 用函数来表示下列编码过程即是:
f(x)=DTx=c f ( x ) = D T x = c
同时, 我们也希望找到一个解码函数, 使得
g(f(x))=g(c)=Dc=DDTx≈x′ g ( f ( x ) ) = g ( c ) = D c = D D T x ≈ x ′
其中 D D 是一个列向量彼此正交的 Rn∗l R n ∗ l 矩阵.
需要指出的是, PCA有两种推导过程, 但它们的结论是一样的.

A. 最大方差理论

---

既然我们需要有损失的把 xn x n 投影成 xl x l , 我们自然地会希望 xl x l 尽可能地保留原样本的特性, 使得投影后的各样本保留最大的区分度, 把样本间的方差最大化.

这里我们先假设原始样本已经做了均值化处理, 即样本的所有特征的均值皆是0. 容易看出, 投影策略对每个样本的统一特征都做了相同的变换, 投影后的所有特征的均值仍为0.

于是投影后样本点的方差便可写为: ∑iDTxixTiD ∑ i D T x i x i T D , 我们要求的矩阵D即是:
D∗=max argD Tr(DTXXTD) subject to DTD=I D ∗ = m a x   a r g D   T r ( D T X X T D )   s u b j e c t   t o   D T D = I
其中X为所有样本点堆叠起来形成的矩阵.

在这里, 我们略去数学证明过程, 我们只需要知道使方差最大的矩阵D即是 XXT X X T 前 l l 个最大的特征值对应的特征向量所组成的矩阵.

B. 最小误差理论

---

同样地, 既然我们需要有损失的进行投影, 我们会希望投影造成的损失尽可能的小. 我们用Frobenius范数来衡量损失的话, 要求的矩阵D即是:
D∗=min argD ∑i,j(xij−DDTxij)2−−−−−−−−−−−−−−−√ subject to DTD=I D ∗ = m i n   a r g D   ∑ i , j ( x j i − D D T x j i ) 2   s u b j e c t   t o   D T D = I

如果我们动手进行数学运算或是证明就能发现, 这里使损失最小的矩阵D仍然是 XXT X X T 前 l l 个最大的特征值对应的特征向量所组成的矩阵.

算法步骤

---

到这里, 我们就可以给出PCA算法的具体步骤了.

1, 对所有样本进行均值化, xi=xi−1m∑mi=1xi x i = x i − 1 m ∑ i = 1 m x i
2. 计算样本的协方差矩阵, XXT X X T
3. 对协方差矩阵进行SVD分解,
4. 取前 l l 个最大特征值的特征向量得到输出(目标矩阵) D D

代码实现

---

在Sklearn等库中提供了PCA的直接实现, 但在这里为了加深印象, 下面的代码采用了逐步实现的办法.

这里选择了剑桥大学提供的AT&T人脸数据集, 因为该数据集大小合适, 有40个人的人脸图像, 每个人有10张不同光照和姿态的照片, 用来做PCA降维刚刚好.
从官网 下载到该数据集后, 我们便可以开工了.

首先需要读取数据. 这里有注意Py中的路径名最好用/来分隔, 用Windows中的\来分隔可能会引起歧义.

我们用OpenCV中的imread()方法先读取图片, 这时候的图片是包含了RGB信息的, 但为了方便起见我们只需要每个像素点的灰度值, 因此我们用cvtColor方法进行转换.

注意到, 这时候我们的图片表示是height*width的一个二维矩阵, 但从上面的分析可以知道我们需要我的样本点是一个一维向量, 因此我们接着用numpy库的reshape函数把二维的图形矩阵变成一列.

FACE_PATH = "F:/Laboratory/PCA_Face/att_faces"  # \\ can be ambiguous
PERSON_NUM = 40
PERSON_FACE_NUM = 10
K = 10  # Number of principle components

def read_data():
    for i in range(1, PERSON_NUM + 1):
        person_path = FACE_PATH + '/s' + str(i)

        for j in range(1, PERSON_FACE_NUM + 1):
            img = cv2.imread(person_path + '/' + str(j) + '.pgm')
            if j == 1:
                raw_img.append(img)
            img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
            height, width = img_gray.shape
            img_col = img_gray.reshape(height * width)
            data_set.append(img_col)
            data_set_label.append(i)
    return height, width

读取数据的工作完成之后, 我们已经拥有了样本集. 这里我们不妨把每个人的照片都打印一张出来认识一下提供数据的优秀志愿者们.

# Print some samples
raw_img=np.hstack(raw_img)
cv2.namedWindow("Image")
cv2.imshow('Image',raw_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

输出如下为:

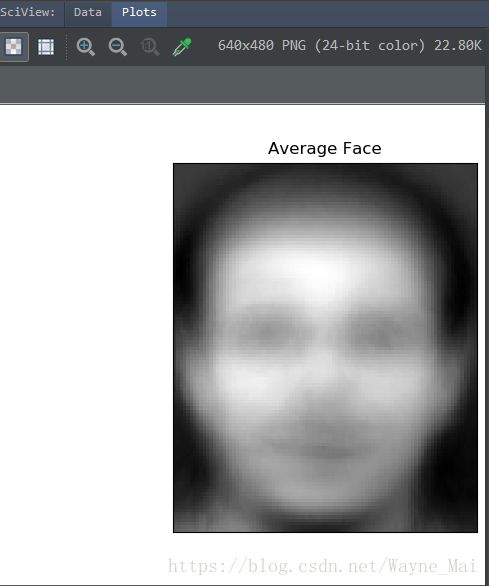
接下来正式进入到前面所述的PCA算法步骤中. 首先把每个样本点都减去均值. 这一均值还有更通俗的称呼”平均脸”. 因此, 我们不妨把平均脸也打印出来看看.

# A preview of average_face
average_face = np.mean(X, axis=0)
fig = plt.figure()
plt.imshow(average_face.reshape((height, width)), cmap=plt.cm.gray)
plt.title("Average Face", size=12)
plt.xticks(())
plt.yticks(())
plt.show()

这里改用matplotlib进行绘图, 得到平均脸的输出如下:

接下来正式进入算法的主要步骤: 减去平均脸, 求出前k个最大的特征值和它们对应的特征向量.

值得一提的是, 求特征向量时需要用到SVD分解. 一开始笔者试图用numpy库的svd分解一个10,000+*10,000+的矩阵, 很快发现即使CPU占用100%跑了五分钟, 仍然跑不出结果. 无奈之下用了sklearn中的TruncatedSVD方法, 它通过Halko (2009)提出的随机化方法来牺牲准确度来降低运算量, 计算出调用时指定的前K个最大特征值和对应的特征向量.

equalization_X = X - average_face
covariance_X = np.cov(equalization_X.transpose())
svd = TruncatedSVD(n_components=K, random_state=44)
svd.fit(covariance_X)

最后, 为了更直观的理解, 我们把主成分还原成图像来可视化. (因为每个主成分都是和样本一样在 Rn R n 空间的)

plt.figure()
for i in range(1, K + 1):
    plt.subplot(2, 5, i)
    plt.imshow(svd.components_[i - 1].reshape(height, width).reshape((height, width)), cmap=plt.cm.gray)
    plt.xticks(())
    plt.yticks(())
plt.show()

最后得到的主成分脸如下:

完整代码

---

import cv2
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import TruncatedSVD

FACE_PATH = "F:/Laboratory/PCA_Face/att_faces"  # \\ can be ambiguous
PERSON_NUM = 40
PERSON_FACE_NUM = 10
K = 10  # Number of principle components

raw_img = []
data_set = []
data_set_label = []


def read_data():
    for i in range(1, PERSON_NUM + 1):
        person_path = FACE_PATH + '/s' + str(i)

        for j in range(1, PERSON_FACE_NUM + 1):
            img = cv2.imread(person_path + '/' + str(j) + '.pgm')
            if j == 1:
                raw_img.append(img)
            img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
            height, width = img_gray.shape
            img_col = img_gray.reshape(height * width)
            data_set.append(img_col)
            data_set_label.append(i)
    return height, width


# Import Data
height, width = read_data()
X = np.array(data_set)
Y = np.array(data_set_label)
n_sample, n_feature = X.shape

# Print some samples
raw_img = np.hstack(raw_img)
cv2.namedWindow("Image")
cv2.imshow('Image', raw_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

# A preview of average_face
average_face = np.mean(X, axis=0)
fig = plt.figure()
plt.imshow(average_face.reshape((height, width)), cmap=plt.cm.gray)
plt.title("Average Face", size=12)
plt.xticks(())
plt.yticks(())
plt.show()

# Calculate
equalization_X = X - average_face
covariance_X = np.cov(equalization_X.transpose())
svd = TruncatedSVD(n_components=K, random_state=44)
svd.fit(covariance_X)

# Print PCA faces
plt.figure()
for i in range(1, K + 1):
    plt.subplot(2, 5, i)
    plt.imshow(svd.components_[i - 1].reshape(height, width).reshape((height, width)), cmap=plt.cm.gray)
    plt.xticks(())
    plt.yticks(())
plt.show()

参考文献

---

• 周志华, 机器学习, 清华大学出版社, 2016年1月第一版, pp.229-231
• Ian Goodfellow等, Deep Learning, 人民邮电出版社, 2017年8月第一版, pp.32-33
• F. Samaria and A. Harter , “Parameterisation of a stochastic model for human face identification”, 2nd IEEE Workshop on Applications of Computer Vision,December 1994, Sarasota (Florida).
• Scikit-learn实例之Pca+Svm人脸识别