强化学习-利用Q-Learning算法玩走方格游戏(C++)
本文通过Q-Learning算法玩走方格游戏的例子和代码,尝试说明Q-Learning的思想与基本实现方法。
随着人工智能的发展,强化学习相关的算法受到越来越多的关注。强化学习是一种无监督学习,通过智能体(Agent)自行根据现实世界及自身的状态(state),决定策略(action),与现实世界交互,改变自身及现实世界的状态(state),并从状态中获取本次执行的策略的奖励(reward),来优化在不同环境及自身状态下的决策。
Q-Learning是强化学习算法家族中应用最广泛的一种算法,也体现着强化学习的基本思想。前些年大火的Alpha-Go程序的思想就是基于Q-Learning算法,加入了众多搜索与优化算法。
走方格游戏的规则是:有一个5*5的方格地图(大小可调),智能体从左上角出发,目标是右下角的出口;地图上有若干地雷,遇到地雷则智能体死亡;智能体可以通过向上下左右四个方向行走到达出口获得游戏胜利。
程序思路:
1、数据结构Q-table:Q-table是一张表,存储着智能体的每一个状态下,执行不同行为时的预期奖励。走方格游戏中,对于固定的一张地图,智能体的状态可以由向量(x,y)表示其位置,现实世界是不变的,所以不算作状态;下面程序中,数组Qtable[x][y][i]就代表智能体在(x,y)位置下执行动作i时的预期奖励,i有上下左右四个值
备注:之前的代码思路是:枚举每一张可能的地图,再枚举每张地图下智能体在每个位置,将向量(地图,x,y)作为状态,但是这样的后果是:存不下!所以处于学习的角度,将地图固定,不算做状态。事实上,用C++计算一5*5的地图的策略只需要0.4秒。
2、算法:优化决策的过程
由马尔科夫决策过程对Qtable进行优化。该过程的核心方程是
Qtable[x][y][i] = Qtable[x][y][i] + rate * ( reward[x1][y1] + max( Qtable[x1][y1][i] ))
即:执行一个策略之后智能体从(x,y)移动到(x1,y1)点,那么在状态(x,y)下执行动作 i 的奖励就是:下一个行为本身的收益 + 走到下一个方格之后,最好的预期收益。具体举例来说,从(x,y)移动到(x1,y1)点,如果(x1,y1)点是地雷,那么收益为负,如果是好吃的,那么收益为正(游戏中没有好吃的,just 举例),这就是“向右走”这一行为本身带来的收益;而走到(x1,y1)之后,可能离终点近了一步,那么收益为正,否则如果走进了死胡同或者走向了起点,那么收益为负,这就是“向右走这一行为的预期收益”。
上式中,rate为一个比例系数,决定了预期收益的权重;本程序中取0.8
3、技巧:贪心系数Greedy = 0.5
Q-learning本质上是贪心算法。但是如果每次都取预期奖励最高的行为去做,那么在训练过程中可能无法探索其他可能的行为,甚至会进入“局部最优”,无法完成游戏。所以,由贪心系数,使得智能体有Greedy的概率采取最优行为,也有一定概率探索新的路径。
4、打分表:表示智能体走到某个位置获得的分数。在走方格游戏中,走到地雷分数为-1,平地为0,终点为5。注意:走到平地必须为0,否则智能体可能会向左走一步得分,再向右走得分,陷入这样的死循环。而且分值不要太大,训练过程中会对得分进行累加,后面可能数值很大
程序采用C++实现
什么?我为什么不用python
python在多循环的整形运算程序上的速度至少也是C++的30倍,运行0.4秒调试一次,和运行10秒调试一次,差距还是蛮大的!
有几个程序中应该注意的问题:
1、所有变量用double,Qtable本身就是double,否则浮点乘整形调试很麻烦
2、一步一步输出Qtable看优化过程对不对
代码如下:
#include
#include
#include
#include
#include
#include
using namespace std;
//宏定义,定义上下左右四个动作的代号
#define up 0
#define down 1
#define left 2
#define right 3
//马尔可夫决策过程公式中的比例系数
double rate = 0.8;
//走到每个位置的分数
//实际上就是存储的地图,0代表可以走,-1代表地雷,5代表终点
int score[5][5] = {0,0,0,-1,0,
0,-1,0,0,0,
-1,0,-1,0,-1,
-1,0,0,0,-1,
0,-1,0,0,5};
//Q-table
double Qtable[5][5][4] = {0};
//记录是否走过这一点,测试结果时使用
int vis[5][5] = {0};
//智能体的位置,
int x = 0;
int y = 0;
//是否到达终点,0不到达,1到达
int dead = 0;
//贪心系数,20表示执行贪心决策的概率为20%
int greedy = 20;
//全局初始化函数
bool game_set(){
//初始化Q-table,智能体不能走出边界,所以再边界上再往外走,就会得到负奖励
for (int i = 0; i <= 4; i++){
Qtable[0][i][up] = -100;
Qtable[4][i][down] = -100;
Qtable[i][0][left] = -100;
Qtable[i][4][right] = -100;
}
//初始化随机数种子
srand(time(0));
return true;
}
//每次训练之前的变量初始化
bool game_init(){
//位置初始化为0,0
x = 0;
y = 0;
dead = 0;
return true;
}
//没用的变量
int cnt = 0;
//获取最大的预期奖励,对应马尔可夫决策过程
//Qtable[x][y][i] = Qtable[x][y][i] + rate * ( reward[x1][y1] + max( Qtable[x1][y1][i] ))
//中的 max( Qtable[x1][y1][i])
double get_expected_max_score(){
double s = -10000;
for (int i = 0; i <= 3; i++)
s = max(s, Qtable[x][y][i]);
return s;
}
//执行一步操作,返回执行动作后的 奖励 ,对应马尔可夫决策过程
//Qtable[x][y][i] = Qtable[x][y][i] + rate * ( reward[x1][y1] + max( Qtable[x1][y1][i] ))
//中的 Qtable[x][y][i] + rate * ( reward[x1][y1] + max( Qtable[x1][y1][i] ))
double game_go(int dir){
//记录现在所在位置
int xx = x, yy = y;
//如果走出了边界,则奖励为0,且x,y的值不变
if (x == 0 && dir == up) {return 0;}
if (x == 4 && dir == down) {return 0;}
if (y == 0 && dir == left) {return 0;}
if (y == 4 && dir == right) {return 0;}
//走到下一步
if (dir == up) x--;
if (dir == down) x++;
if (dir == right) y++;
if (dir == left) y--;
//如果到了终点,返回到达终点的奖励
if (x == 4 && y == 4){
dead = 1;
return score[x][y];
}
//得到执行动作后的预期奖励,见函数说明
double tmp = get_expected_max_score();
//对应马尔可夫决策过程
//Qtable[x][y][i] = Qtable[x][y][i] + rate * ( reward[x1][y1] + max( Qtable[x1][y1][i] ))
//中的 reward[x1][y1] + max( Qtable[x1][y1][i] )
return score[x][y] + 1.0 * rate * tmp;
}
//训练结果测试
void game_final_test(){
//本局游戏初始化
game_init();
//当没有走到终点时
while (!(x == 4 && y == 4)){
int op = 0;
//选取Qtable中奖励最大的行为执行
double maxx = -1000000;
for (int i = 0; i < 4; i++)
maxx = max(maxx + 0.0, Qtable[x][y][i]);
for (int i = 0; i < 4; i++)
if (maxx == Qtable[x][y][i])
op = i;
game_go(op);
//如果走到了一个点,记录这个点的vis = 1, 方便输出观察
vis[x][y] = 1;
}
//输出,带有 @ 符号的代表智能体选择的路径
for (int i = 0 ; i <= 4; i++){
for (int j = 0; j <= 4; j++){
cout< 0){
//游戏初始化
game_init();
episode--;
int j = 0;
//每轮游戏走50步,走到终点或者走够50步时结束
while(j < 50){
j++;
//operation,代表下一步要执行的行为
int op;
//记录现在的位置
int xx = x, yy = y;
//一定概率下,随机选择行为
if (rand() % 101 > greedy){
op = rand() % 4;
}
//一定概率下,走最优解
else{
int maxx = -1000000;
for (int i = 0; i < 4; i++)
maxx = max(maxx + 0.0, Qtable[x][y][i]);
for (int i = 0; i < 4; i++)
if (maxx == Qtable[x][y][i])
op = i;
}
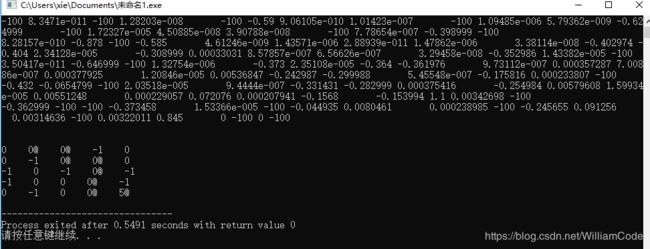
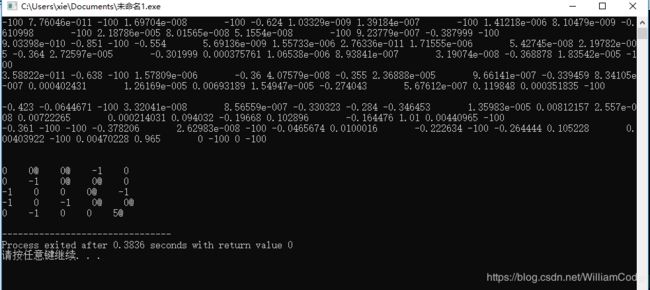
//if (op == 0) cout<<"up"< 地图可以随意改动,附几张地图的测试结果
效果还是不错的,最终的训练结果Qtable中,需要只要是正值的点,都是可以走的。因为加入了随机数,所以训练结果可能不同,但是在很大概率下,智能体能够选择最短路径;因为终点的大奖励是一步一步传播到其他的点,越远的点,获得来自终点的奖励就越少。
这就是Q-Learning算法
很明显,Q-Learning算法很消耗内存,对于状态少的状态,可以存储,但是对于围棋那样,棋盘状态千变万化,状态极多的活动,Q-Learning是无法计算的。更致命的是,现实世界总是连续的,而Qtable是离散的,这也使其很难处理复杂问题
但转念一想,Qtable的作用就是将一个描述状态的向量映射到另一个行为向量,这不正是深度神经网路擅长的吗?
所以,深度强化学习 出生了!
最近在学,过几天更新吧!