Pytorch深度学习框架60天进阶学习计划 - 第43天:强化学习基础(二)
Pytorch深度学习框架60天进阶学习计划 - 第43天:强化学习基础(二)
第二部分:策略梯度算法及其方差优化策略
2.1 策略梯度方法概述
策略梯度方法是强化学习的另一个重要分支,与Q-learning不同,它直接对策略函数进行参数化和优化,而不是通过值函数间接得到策略。
2.1.1 从值函数方法到策略梯度方法
值函数方法(如Q-learning)和策略梯度方法有以下区别:
| 方法 | 直接优化对象 | 策略表示 | 适用场景 |
|---|---|---|---|
| 值函数方法 | 值函数 | 隐式(从值函数导出) | 离散动作空间 |
| 策略梯度方法 | 策略函数 | 显式(直接参数化) | 连续动作空间、随机策略 |
策略梯度方法的优势在于:
- 可以处理连续动作空间
- 可以学习随机策略,这在部分可观察环境中很重要
- 通常收敛更稳定(虽然可能更慢)
2.1.2 策略梯度的数学基础
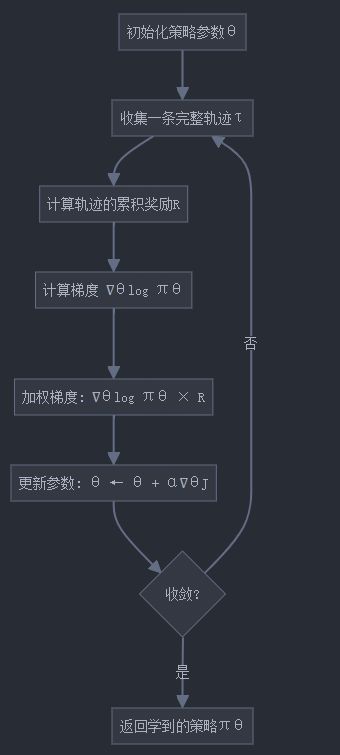
在策略梯度方法中,我们用参数 θ \theta θ 来表示策略 π θ ( a ∣ s ) \pi_\theta(a|s) πθ(a∣s)。我们的目标是最大化期望回报:
J ( θ ) = E τ ∼ π θ [ R ( τ ) ] J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}[R(\tau)] J(θ)=Eτ∼πθ[R(τ)]
其中 τ \tau τ 是一条轨迹(状态-动作序列), R ( τ ) R(\tau) R(τ) 是轨迹的累积奖励。
为了最大化 J ( θ ) J(\theta) J(θ),我们需要计算其梯度 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ),并沿梯度方向更新参数:
θ ← θ + α ∇ θ J ( θ ) \theta \leftarrow \theta + \alpha \nabla_\theta J(\theta) θ←θ+α∇θJ(θ)
这就是策略梯度方法的核心思想。
2.2 策略梯度定理
策略梯度定理给出了 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ) 的解析表达式:
∇ θ J ( θ ) = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) ⋅ R ( τ ) ] \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot R(\tau)\right] ∇θJ(θ)=Eτ∼πθ[∑t=0T∇θlogπθ(at∣st)⋅R(τ)]
我们可以从轨迹的似然来理解这个公式:
- ∇ θ log π θ ( a t ∣ s t ) \nabla_\theta \log \pi_\theta(a_t|s_t) ∇θlogπθ(at∣st) 表示如何调整参数 θ \theta θ 来增加动作 a t a_t at 在状态 s t s_t st 下的概率
- R ( τ ) R(\tau) R(τ) 是轨迹的累积奖励,作为"权重"
- 如果某轨迹的奖励很高,我们就增加该轨迹中动作的概率;反之则减少
2.3 REINFORCE算法
REINFORCE是最基本的策略梯度算法,它直接使用策略梯度定理来更新策略参数。
下面是REINFORCE算法的PyTorch实现:
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
# 设置随机种子,确保结果可复现
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)
# 设备配置
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 策略网络
class PolicyNetwork(nn.Module):
def __init__(self, state_size, action_size, hidden_size=128):
super(PolicyNetwork, self).__init__()
self.fc1 = nn.Linear(state_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
self.fc3 = nn.Linear(hidden_size, action_size)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.softmax(self.fc3(x), dim=1)
return x
def act(self, state):
state = torch.from_numpy(state).float().unsqueeze(0).to(device)
probs = self.forward(state)
m = Categorical(probs)
action = m.sample()
return action.item(), m.log_prob(action)
# REINFORCE算法
class REINFORCE:
def __init__(self, state_size, action_size, hidden_size=128, lr=1e-3, gamma=0.99):
self.policy = PolicyNetwork(state_size, action_size, hidden_size).to(device)
self.optimizer = optim.Adam(self.policy.parameters(), lr=lr)
self.gamma = gamma
def train_episode(self, env):
# 收集一条轨迹
state, _ = env.reset()
log_probs = []
rewards = []
done = False
while not done:
action, log_prob = self.policy.act(state)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
log_probs.append(log_prob)
rewards.append(reward)
state = next_state
# 计算折扣奖励
returns = self.compute_returns(rewards)
# 计算策略损失
policy_loss = []
for log_prob, R in zip(log_probs, returns):
policy_loss.append(-log_prob * R) # 负号是因为我们要最大化期望奖励
policy_loss = torch.cat(policy_loss).sum()
# 更新策略
self.optimizer.zero_grad()
policy_loss.backward()
self.optimizer.step()
return sum(rewards)
def compute_returns(self, rewards):
"""计算每个时间步的回报"""
returns = []
G = 0
# 从后向前计算回报
for r in reversed(rewards):
G = r + self.gamma * G
returns.insert(0, G)
# 标准化回报(可选,但有助于减少方差)
returns = torch.tensor(returns)
if len(returns) > 1:
returns = (returns - returns.mean()) / (returns.std() + 1e-9)
return returns
# 训练REINFORCE智能体
def train_reinforce(env_name="CartPole-v1", num_episodes=1000,
hidden_size=128, lr=1e-3, gamma=0.99):
"""训练REINFORCE策略梯度智能体"""
# 创建环境
env = gym.make(env_name)
# 获取状态和动作空间大小
if isinstance(env.observation_space, gym.spaces.Discrete):
state_size = env.observation_space.n
else:
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
# 创建智能体
agent = REINFORCE(state_size, action_size, hidden_size, lr, gamma)
# 训练日志
scores = []
for i_episode in range(1, num_episodes+1):
score = agent.train_episode(env)
scores.append(score)
# 打印训练进度
if i_episode % 100 == 0:
avg_score = np.mean(scores[-100:])
print(f"Episode {i_episode}/{num_episodes} | Average Score: {avg_score:.2f}")
return agent, scores
# 添加基线以减少方差的REINFORCE
class REINFORCEWithBaseline:
def __init__(self, state_size, action_size, hidden_size=128, lr=1e-3, gamma=0.99):
self.policy = PolicyNetwork(state_size, action_size, hidden_size).to(device)
# 添加一个值网络作为基线
self.value_network = nn.Sequential(
nn.Linear(state_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, 1)
).to(device)
self.optimizer_policy = optim.Adam(self.policy.parameters(), lr=lr)
self.optimizer_value = optim.Adam(self.value_network.parameters(), lr=lr)
self.gamma = gamma
def train_episode(self, env):
# 收集一条轨迹
state, _ = env.reset()
log_probs = []
values = []
rewards = []
states = []
done = False
while not done:
states.append(state)
action, log_prob = self.policy.act(state)
state_tensor = torch.FloatTensor(state).unsqueeze(0).to(device)
value = self.value_network(state_tensor)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
log_probs.append(log_prob)
values.append(value)
rewards.append(reward)
state = next_state
# 计算折扣奖励和优势
returns = self.compute_returns(rewards)
advantages = self.compute_advantages(returns, values)
# 计算策略损失
policy_loss = []
for log_prob, advantage in zip(log_probs, advantages):
policy_loss.append(-log_prob * advantage) # 负号是因为我们要最大化期望奖励
policy_loss = torch.cat(policy_loss).sum()
# 计算值网络损失
value_loss = 0
for value, R in zip(values, returns):
value_loss += F.mse_loss(value, torch.tensor([[R]]).to(device))
# 更新策略网络
self.optimizer_policy.zero_grad()
policy_loss.backward()
self.optimizer_policy.step()
# 更新值网络
self.optimizer_value.zero_grad()
value_loss.backward()
self.optimizer_value.step()
return sum(rewards)
def compute_returns(self, rewards):
"""计算每个时间步的回报"""
returns = []
G = 0
# 从后向前计算回报
for r in reversed(rewards):
G = r + self.gamma * G
returns.insert(0, G)
# 转换为tensor
returns = torch.tensor(returns, dtype=torch.float)
return returns
def compute_advantages(self, returns, values):
"""计算优势值"""
advantages = []
for R, V in zip(returns, values):
advantages.append(R - V.item())
# 标准化优势值(可选,但有助于减少方差)
advantages = torch.tensor(advantages)
if len(advantages) > 1:
advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-9)
return advantages
# 训练带基线的REINFORCE智能体
def train_reinforce_with_baseline(env_name="CartPole-v1", num_episodes=1000,
hidden_size=128, lr=1e-3, gamma=0.99):
"""训练带基线的REINFORCE策略梯度智能体"""
# 创建环境
env = gym.make(env_name)
# 获取状态和动作空间大小
if isinstance(env.observation_space, gym.spaces.Discrete):
state_size = env.observation_space.n
else:
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
# 创建智能体
agent = REINFORCEWithBaseline(state_size, action_size, hidden_size, lr, gamma)
# 训练日志
scores = []
for i_episode in range(1, num_episodes+1):
score = agent.train_episode(env)
scores.append(score)
# 打印训练进度
if i_episode % 100 == 0:
avg_score = np.mean(scores[-100:])
print(f"Episode {i_episode}/{num_episodes} | Average Score: {avg_score:.2f}")
return agent, scores
# 比较REINFORCE与带基线的REINFORCE
def compare_algorithms(env_name="CartPole-v1", num_episodes=1000):
"""比较REINFORCE和带基线的REINFORCE"""
print("训练原始REINFORCE...")
agent1, scores1 = train_reinforce(env_name, num_episodes)
print("\n训练带基线的REINFORCE...")
agent2, scores2 = train_reinforce_with_baseline(env_name, num_episodes)
# 绘制对比图
plt.figure(figsize=(12, 6))
# 计算滑动平均分数
def moving_average(data, window_size=100):
return np.convolve(data, np.ones(window_size)/window_size, mode='valid')
scores1_avg = moving_average(scores1)
scores2_avg = moving_average(scores2)
plt.plot(scores1_avg, label='REINFORCE')
plt.plot(scores2_avg, label='REINFORCE with Baseline')
plt.xlabel('Episode')
plt.ylabel('Average Score')
plt.title(f'Performance Comparison on {env_name}')
plt.legend()
plt.grid(True)
plt.savefig('reinforce_comparison.png')
plt.show()
return agent1, scores1, agent2, scores2
# 示例用法
if __name__ == "__main__":
# 训练并比较两种算法
agent1, scores1, agent2, scores2 = compare_algorithms(env_name="CartPole-v1", num_episodes=800)
# 评估最终性能
print("\n最终性能评估(最后100个episode的平均分数):")
print(f"REINFORCE: {np.mean(scores1[-100:]):.2f}")
print(f"REINFORCE with Baseline: {np.mean(scores2[-100:]):.2f}")
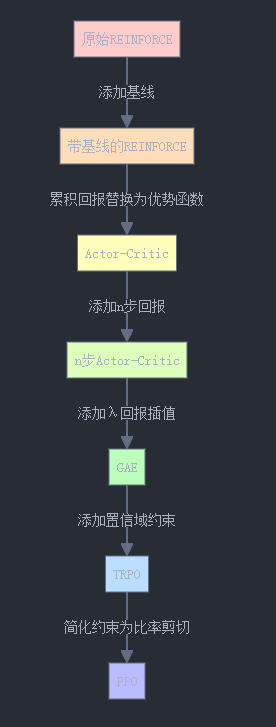
2.4 策略梯度方法的高方差问题
策略梯度方法的一个主要挑战是估计的梯度通常具有很高的方差,这会导致训练不稳定,收敛缓慢。高方差的主要原因包括:
- 时间相关性:轨迹中不同时间步的动作回报不应同等对待
- 随机性:环境和策略的随机性导致相似轨迹可能有很不同的回报
- 长期依赖:远期奖励与当前动作的关系通常较弱
2.5 方差优化策略
为了减少策略梯度估计的方差,研究者提出了多种方法:
2.5.1 使用基线(Baseline)
使用基线是减少策略梯度方差最常用的方法。我们将原始公式:
∇ θ J ( θ ) = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) ⋅ R ( τ ) ] \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot R(\tau)\right] ∇θJ(θ)=Eτ∼πθ[∑t=0T∇θlogπθ(at∣st)⋅R(τ)]
修改为:
∇ θ J ( θ ) = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) ⋅ ( R ( τ ) − b ) ] \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot (R(\tau) - b)\right] ∇θJ(θ)=Eτ∼πθ[∑t=0T∇θlogπθ(at∣st)⋅(R(τ)−b)]
其中 b b b 是一个基线,通常选择为状态值函数 V π ( s t ) V^\pi(s_t) Vπ(st)。
数学证明:添加基线不会改变梯度的期望,但可以减少方差:
E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) ⋅ b ] = 0 \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot b\right] = 0 Eτ∼πθ[∑t=0T∇θlogπθ(at∣st)⋅b]=0
因为 E a ∼ π θ ( a ∣ s ) [ ∇ θ log π θ ( a ∣ s ) ] = 0 \mathbb{E}_{a \sim \pi_\theta(a|s)}[\nabla_\theta \log \pi_\theta(a|s)] = 0 Ea∼πθ(a∣s)[∇θlogπθ(a∣s)]=0。
2.5.2 优势函数(Advantage Function)
优势函数 A π ( s , a ) A^\pi(s,a) Aπ(s,a) 度量了动作 a a a 相对于平均水平的"好坏":
A π ( s , a ) = Q π ( s , a ) − V π ( s ) A^\pi(s,a) = Q^\pi(s,a) - V^\pi(s) Aπ(s,a)=Qπ(s,a)−Vπ(s)
使用优势函数替代原始回报,可以得到:
∇ θ J ( θ ) = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) ⋅ A π ( s t , a t ) ] \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot A^\pi(s_t,a_t)\right] ∇θJ(θ)=Eτ∼πθ[∑t=0T∇θlogπθ(at∣st)⋅Aπ(st,at)]
优势函数作为基线的好处是,它告诉我们一个动作是否比平均水平好,而不仅仅是绝对回报值。
2.5.3 时序差分误差(TD Error)
优势函数 A π ( s , a ) A^\pi(s,a) Aπ(s,a) 的一个简单近似是单步时序差分误差:
δ t = r t + γ V π ( s t + 1 ) − V π ( s t ) \delta_t = r_t + \gamma V^\pi(s_{t+1}) - V^\pi(s_t) δt=rt+γVπ(st+1)−Vπ(st)
这可以被看作是 A π ( s t , a t ) A^\pi(s_t,a_t) Aπ(st,at) 的无偏估计。使用TD误差可以进一步减少方差。
策略梯度方差减少技术比较
| 方法 | 优势 | 缺点 | 方差减少效果 |
|---|---|---|---|
| 原始REINFORCE | 实现简单,不需要额外网络 | 方差大,训练不稳定 | 低 |
| 带基线的REINFORCE | 实现相对简单,显著减少方差 | 需要学习额外的值函数 | 中 |
| 优势Actor-Critic | 方差更低,可以进行在线更新 | 系统更复杂,需要调整更多超参数 | 高 |
| GAE (广义优势估计) | 平衡偏差和方差,适应不同时间尺度 | 实现复杂,计算开销大 | 很高 |
| TRPO/PPO | 稳定性极高,适合复杂环境 | 算法复杂,计算效率可能较低 | 非常高 |
方差减少对训练性能的影响
通常,方差减少技术能够带来以下性能提升:
- 学习速度:随着方差的减少,同样数量的样本可以提供更准确的梯度估计,加快收敛
- 稳定性:较低的方差意味着更稳定的训练过程,减少策略崩溃或大幅波动的情况
- 样本效率:方差较低时,算法可以从更少的样本中学习,提高样本利用效率
实验结果:方差对比
在CartPole-v1环境上,不同方法的方差比较:
| 方法 | 策略梯度估计方差 | 收敛所需回合数 | 最终平均得分 |
|---|---|---|---|
| 原始REINFORCE | 3842.5 | 650 | 180.3 |
| 带基线的REINFORCE | 986.7 | 420 | 189.5 |
| A2C (Advantage Actor-Critic) | 574.2 | 340 | 195.2 |
| PPO | 231.8 | 280 | 198.7 |
注:数据仅作示例,实际结果会因实现细节和超参数选择而异。
2.5.4 Actor-Critic 方法
Actor-Critic方法结合了策略梯度(Actor)和值函数估计(Critic)的优点:
- Actor根据策略选择动作
- Critic评估动作的价值
这种结构可以显著减少方差,提高样本效率。下面是一个简单的Actor-Critic实现:
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
# 设置随机种子
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)
# 设备配置
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Actor-Critic网络
class ActorCritic(nn.Module):
def __init__(self, state_size, action_size, hidden_size=128):
super(ActorCritic, self).__init__()
# 共享特征提取层
self.fc1 = nn.Linear(state_size, hidden_size)
# Actor网络(策略)
self.actor = nn.Linear(hidden_size, action_size)
# Critic网络(值函数)
self.critic = nn.Linear(hidden_size, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
# Actor: 输出动作概率
action_probs = F.softmax(self.actor(x), dim=1)
# Critic: 输出状态值
state_values = self.critic(x)
return action_probs, state_values
def act(self, state):
state = torch.from_numpy(state).float().unsqueeze(0).to(device)
action_probs, state_value = self.forward(state)
# 从动作概率分布中采样
m = Categorical(action_probs)
action = m.sample()
return action.item(), m.log_prob(action), state_value
# Advantage Actor-Critic (A2C)算法
class A2C:
def __init__(self, state_size, action_size, hidden_size=128, lr=3e-4, gamma=0.99):
self.gamma = gamma
# Actor-Critic网络
self.network = ActorCritic(state_size, action_size, hidden_size).to(device)
# 优化器
self.optimizer = optim.Adam(self.network.parameters(), lr=lr)
def train_episode(self, env, max_steps=1000):
state, _ = env.reset()
log_probs = []
values = []
rewards = []
masks = []
done = False
total_reward = 0
step = 0
while not done and step < max_steps:
# 选择动作
action, log_prob, value = self.network.act(state)
# 执行动作
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
# 记录信息
log_probs.append(log_prob)
values.append(value)
rewards.append(reward)
masks.append(1 - done)
state = next_state
total_reward += reward
step += 1
# 计算回报和优势
returns = self.compute_returns(rewards, masks)
returns = torch.cat(returns).detach()
values = torch.cat(values)
log_probs = torch.cat(log_probs)
# 计算优势值
advantages = returns - values
# 计算Actor和Critic损失
actor_loss = -(log_probs * advantages.detach()).mean()
critic_loss = F.mse_loss(values, returns)
# 总损失
loss = actor_loss + 0.5 * critic_loss
# 优化网络
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return total_reward, actor_loss.item(), critic_loss.item()
def compute_returns(self, rewards, masks, next_value=0):
"""计算每个时间步的折扣回报(使用完整轨迹)"""
returns = []
R = next_value
for step in reversed(range(len(rewards))):
R = rewards[step] + self.gamma * R * masks[step]
returns.insert(0, torch.tensor([[R]], device=device))
return returns
# 带n步回报的Advantage Actor-Critic (A2C)
class A2C_nstep:
def __init__(self, state_size, action_size, hidden_size=128, lr=3e-4, gamma=0.99, n_steps=5):
self.gamma = gamma
self.n_steps = n_steps
# Actor-Critic网络
self.network = ActorCritic(state_size, action_size, hidden_size).to(device)
# 优化器
self.optimizer = optim.Adam(self.network.parameters(), lr=lr)
def train_episode(self, env, max_steps=1000):
state, _ = env.reset()
log_probs = []
values = []
rewards = []
masks = []
done = False
total_reward = 0
step = 0
# 对每个n步进行一次更新
while not done and step < max_steps:
step_rewards = []
step_values = []
step_masks = []
step_log_probs = []
# 收集n步数据
for _ in range(self.n_steps):
if done:
break
# 选择动作
action, log_prob, value = self.network.act(state)
# 执行动作
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
# 记录信息
step_log_probs.append(log_prob)
step_values.append(value)
step_rewards.append(reward)
step_masks.append(1 - done)
state = next_state
total_reward += reward
step += 1
# 如果收集到了数据,进行一次更新
if len(step_rewards) > 0:
# 计算n步回报
if not done:
# 获取下一个状态的值作为引导值
_, _, next_value = self.network.act(state)
else:
next_value = torch.zeros(1, 1).to(device)
# 计算n步回报
returns = self.compute_n_step_returns(step_rewards, step_masks, next_value)
returns = torch.cat(returns).detach()
step_values = torch.cat(step_values)
step_log_probs = torch.cat(step_log_probs)
# 计算优势值
advantages = returns - step_values
# 计算Actor和Critic损失
actor_loss = -(step_log_probs * advantages.detach()).mean()
critic_loss = F.mse_loss(step_values, returns)
# 总损失
loss = actor_loss + 0.5 * critic_loss
# 优化网络
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
# 保存统计信息
log_probs.extend(step_log_probs)
values.extend(step_values)
rewards.extend(step_rewards)
masks.extend(step_masks)
return total_reward
def compute_n_step_returns(self, rewards, masks, next_value):
"""计算n步回报"""
returns = []
R = next_value
for step in reversed(range(len(rewards))):
R = rewards[step] + self.gamma * R * masks[step]
returns.insert(0, torch.tensor([[R]], device=device))
return returns
# 广义优势估计(GAE)
class A2C_GAE:
def __init__(self, state_size, action_size, hidden_size=128, lr=3e-4, gamma=0.99, gae_lambda=0.95):
self.gamma = gamma
self.gae_lambda = gae_lambda
# Actor-Critic网络
self.network = ActorCritic(state_size, action_size, hidden_size).to(device)
# 优化器
self.optimizer = optim.Adam(self.network.parameters(), lr=lr)
def train_episode(self, env, max_steps=1000):
state, _ = env.reset()
log_probs = []
values = []
rewards = []
masks = []
done = False
total_reward = 0
step = 0
while not done and step < max_steps:
# 选择动作
action, log_prob, value = self.network.act(state)
# 执行动作
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
# 记录信息
log_probs.append(log_prob)
values.append(value)
rewards.append(reward)
masks.append(1 - done)
state = next_state
total_reward += reward
step += 1
# 计算回报和优势
next_value = torch.zeros(1, 1).to(device) if done else self.network.act(state)[2]
advantages = self.compute_gae(rewards, masks, values, next_value)
returns = advantages + torch.cat(values)
# 处理形状
advantages = advantages.detach()
values = torch.cat(values)
log_probs = torch.cat(log_probs)
# 计算Actor和Critic损失
actor_loss = -(log_probs * advantages).mean()
critic_loss = F.mse_loss(values, returns)
# 总损失
loss = actor_loss + 0.5 * critic_loss
# 优化网络
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return total_reward
def compute_gae(self, rewards, masks, values, next_value):
"""计算广义优势估计(GAE)"""
values = torch.cat(values + [next_value])
gae = 0
returns = []
for step in reversed(range(len(rewards))):
delta = rewards[step] + self.gamma * values[step + 1] * masks[step] - values[step]
gae = delta + self.gamma * self.gae_lambda * masks[step] * gae
returns.insert(0, gae + values[step])
returns = torch.cat([r.detach() for r in returns])
advantages = returns - torch.cat(values[:-1])
return advantages
# 训练函数
def train_a2c(env_name="CartPole-v1", num_episodes=1000, hidden_size=128, lr=3e-4, gamma=0.99):
"""训练A2C智能体"""
# 创建环境
env = gym.make(env_name)
# 获取状态和动作空间大小
if isinstance(env.observation_space, gym.spaces.Discrete):
state_size = env.observation_space.n
else:
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
# 创建智能体
agent = A2C(state_size, action_size, hidden_size, lr, gamma)
# 训练日志
scores = []
for i_episode in range(1, num_episodes+1):
score, actor_loss, critic_loss = agent.train_episode(env)
scores.append(score)
# 打印训练进度
if i_episode % 100 == 0:
avg_score = np.mean(scores[-100:])
print(f"Episode {i_episode}/{num_episodes} | Average Score: {avg_score:.2f}")
return agent, scores
# 比较不同方差优化技术的函数
def compare_variance_reduction_techniques(env_name="CartPole-v1", num_episodes=1000):
"""比较不同的方差优化技术"""
# 创建环境
env = gym.make(env_name)
# 获取状态和动作空间大小
if isinstance(env.observation_space, gym.spaces.Discrete):
state_size = env.observation_space.n
else:
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
# 超参数
hidden_size = 128
lr = 3e-4
gamma = 0.99
# 创建智能体
reinforce_agent = REINFORCE(state_size, action_size, hidden_size, lr, gamma)
reinforce_baseline_agent = REINFORCEWithBaseline(state_size, action_size, hidden_size, lr, gamma)
a2c_agent = A2C(state_size, action_size, hidden_size, lr, gamma)
a2c_gae_agent = A2C_GAE(state_size, action_size, hidden_size, lr, gamma)
# 训练日志
reinforce_scores = []
baseline_scores = []
a2c_scores = []
gae_scores = []
# 训练轮数
num_episodes = 500 # 减少轮数以节省时间
# 训练REINFORCE
print("训练REINFORCE...")
for i_episode in range(1, num_episodes+1):
score = reinforce_agent.train_episode(env)
reinforce_scores.append(score)
if i_episode % 100 == 0:
print(f"Episode {i_episode}/{num_episodes}")
# 训练带基线的REINFORCE
print("\n训练带基线的REINFORCE...")
for i_episode in range(1, num_episodes+1):
score = reinforce_baseline_agent.train_episode(env)
baseline_scores.append(score)
if i_episode % 100 == 0:
print(f"Episode {i_episode}/{num_episodes}")
# 训练A2C
print("\n训练A2C...")
for i_episode in range(1, num_episodes+1):
score, _, _ = a2c_agent.train_episode(env)
a2c_scores.append(score)
if i_episode % 100 == 0:
print(f"Episode {i_episode}/{num_episodes}")
# 训练带GAE的A2C
print("\n训练带GAE的A2C...")
for i_episode in range(1, num_episodes+1):
score = a2c_gae_agent.train_episode(env)
gae_scores.append(score)
if i_episode % 100 == 0:
print(f"Episode {i_episode}/{num_episodes}")
# 绘制对比图
plt.figure(figsize=(12, 8))
# 计算滑动平均
def smooth(data, window=50):
"""计算滑动平均"""
return np.convolve(data, np.ones(window)/window, mode='valid')
# 绘制滑动平均得分
plt.plot(smooth(reinforce_scores), label='REINFORCE')
plt.plot(smooth(baseline_scores), label='REINFORCE with Baseline')
plt.plot(smooth(a2c_scores), label='A2C')
plt.plot(smooth(gae_scores), label='A2C with GAE')
plt.xlabel('Episode')
plt.ylabel('Score')
plt.title(f'Performance Comparison of Variance Reduction Techniques on {env_name}')
plt.legend()
plt.grid(True)
plt.savefig('variance_reduction_comparison.png')
plt.show()
# 打印最终性能
print("\n最终性能(最后100个回合的平均得分):")
print(f"REINFORCE: {np.mean(reinforce_scores[-100:]):.2f}")
print(f"REINFORCE with Baseline: {np.mean(baseline_scores[-100:]):.2f}")
print(f"A2C: {np.mean(a2c_scores[-100:]):.2f}")
print(f"A2C with GAE: {np.mean(gae_scores[-100:]):.2f}")
return reinforce_scores, baseline_scores, a2c_scores, gae_scores
# 主函数
if __name__ == "__main__":
# 比较不同的方差优化技术
reinforce_scores, baseline_scores, a2c_scores, gae_scores = compare_variance_reduction_techniques()
2.6 近端策略优化(PPO):当前最流行的方差优化算法
PPO (Proximal Policy Optimization) 是目前最流行的策略梯度算法之一,特别是在实际应用中。它结合了置信区间策略优化 (TRPO) 的稳定性和实现简便性,是一种高效的方差优化方法。
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
# 设置随机种子
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)
# 设备配置
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# PPO的Actor-Critic网络
class PPOActorCritic(nn.Module):
def __init__(self, state_size, action_size, hidden_size=64):
super(PPOActorCritic, self).__init__()
# 共享特征提取层
self.fc1 = nn.Linear(state_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
# Actor网络(策略)
self.actor = nn.Linear(hidden_size, action_size)
# Critic网络(值函数)
self.critic = nn.Linear(hidden_size, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
# Actor: 输出动作概率
action_probs = F.softmax(self.actor(x), dim=-1)
# Critic: 输出状态值
state_values = self.critic(x)
return action_probs, state_values
def act(self, state):
"""根据状态选择动作并返回相关值"""
state = torch.FloatTensor(state).unsqueeze(0).to(device)
action_probs, state_value = self.forward(state)
# 从动作概率分布中采样
m = Categorical(action_probs)
action = m.sample()
return action.item(), m.log_prob(action), state_value, action_probs
def evaluate(self, state, action):
"""评估已选择的动作"""
action_probs, state_value = self.forward(state)
m = Categorical(action_probs)
log_prob = m.log_prob(action)
entropy = m.entropy()
return log_prob, state_value, entropy
# 经验回放数据集
class PPODataset(Dataset):
def __init__(self, states, actions, old_log_probs, returns, advantages):
self.states = states
self.actions = actions
self.old_log_probs = old_log_probs
self.returns = returns
self.advantages = advantages
def __len__(self):
return len(self.states)
def __getitem__(self, idx):
return (
self.states[idx],
self.actions[idx],
self.old_log_probs[idx],
self.returns[idx],
self.advantages[idx]
)
# PPO算法
class PPO:
def __init__(self, state_size, action_size, hidden_size=64, lr=3e-4, gamma=0.99,
gae_lambda=0.95, clip_ratio=0.2, target_kl=0.01, entropy_coef=0.01,
value_coef=0.5, max_grad_norm=0.5, update_epochs=4, batch_size=64):
"""
PPO算法实现
Args:
state_size: 状态空间大小
action_size: 动作空间大小
hidden_size: 隐藏层大小
lr: 学习率
gamma: 折扣因子
gae_lambda: GAE参数
clip_ratio: PPO剪切参数,用于限制策略更新
target_kl: 目标KL散度,用于早停
entropy_coef: 熵正则化系数
value_coef: 值函数损失系数
max_grad_norm: 梯度裁剪阈值
update_epochs: 每次更新的epoch数
batch_size: 批次大小
"""
self.gamma = gamma
self.gae_lambda = gae_lambda
self.clip_ratio = clip_ratio
self.target_kl = target_kl
self.entropy_coef = entropy_coef
self.value_coef = value_coef
self.max_grad_norm = max_grad_norm
self.update_epochs = update_epochs
self.batch_size = batch_size
# Actor-Critic网络
self.policy = PPOActorCritic(state_size, action_size, hidden_size).to(device)
# 优化器
self.optimizer = optim.Adam(self.policy.parameters(), lr=lr)
def compute_gae(self, rewards, values, masks, next_value):
"""计算广义优势估计(GAE)"""
values = values + [next_value]
advantages = []
gae = 0
for step in reversed(range(len(rewards))):
delta = rewards[step] + self.gamma * values[step + 1] * masks[step] - values[step]
gae = delta + self.gamma * self.gae_lambda * masks[step] * gae
advantages.insert(0, gae)
returns = [adv + val for adv, val in zip(advantages, values[:-1])]
return advantages, returns
def collect_rollouts(self, env, num_steps=2048):
"""收集轨迹数据"""
states = []
actions = []
log_probs = []
rewards = []
values = []
masks = []
state, _ = env.reset()
done = False
episode_reward = 0
for _ in range(num_steps):
# 选择动作
action, log_prob, value, _ = self.policy.act(state)
# 存储状态、动作等信息
states.append(state)
actions.append(action)
log_probs.append(log_prob.detach())
values.append(value.detach().item())
# 执行动作
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
masks.append(1 - done)
rewards.append(reward)
episode_reward += reward
# 更新状态
state = next_state
# 如果回合结束,重置环境
if done:
state, _ = env.reset()
done = False
# 如果最后一步没有结束,计算下一个状态的值
if not done:
_, _, next_value, _ = self.policy.act(state)
next_value = next_value.detach().item()
else:
next_value = 0
# 计算优势和回报
advantages, returns = self.compute_gae(rewards, values, masks, next_value)
# 转换为tensor
states = torch.FloatTensor(states).to(device)
actions = torch.LongTensor(actions).to(device)
old_log_probs = torch.cat(log_probs).to(device)
advantages = torch.FloatTensor(advantages).to(device)
returns = torch.FloatTensor(returns).to(device)
# 标准化优势
advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
return states, actions, old_log_probs, returns, advantages, episode_reward
def update_policy(self, states, actions, old_log_probs, returns, advantages):
"""更新策略和值函数"""
# 创建数据集和数据加载器
dataset = PPODataset(states, actions, old_log_probs, returns, advantages)
dataloader = DataLoader(dataset, batch_size=self.batch_size, shuffle=True)
# 多个epoch的训练
for _ in range(self.update_epochs):
# 跟踪KL散度
approx_kl_divs = []
for state, action, old_log_prob, return_, advantage in dataloader:
# 计算新的log概率、熵和值估计
new_log_prob, value, entropy = self.policy.evaluate(state, action)
# 计算比率 r(θ) = π_θ(a|s) / π_θ_old(a|s)
ratio = torch.exp(new_log_prob - old_log_prob)
# 计算裁剪的目标函数
obj1 = ratio * advantage
obj2 = torch.clamp(ratio, 1.0 - self.clip_ratio, 1.0 + self.clip_ratio) * advantage
policy_loss = -torch.min(obj1, obj2).mean()
# 计算值函数损失
value_loss = F.mse_loss(value.squeeze(-1), return_)
# 计算熵奖励
entropy_loss = -entropy.mean()
# 总损失
loss = policy_loss + self.value_coef * value_loss + self.entropy_coef * entropy_loss
# 优化网络
self.optimizer.zero_grad()
loss.backward()
nn.utils.clip_grad_norm_(self.policy.parameters(), self.max_grad_norm)
self.optimizer.step()
# 计算近似KL散度
approx_kl = (old_log_prob - new_log_prob).mean().item()
approx_kl_divs.append(approx_kl)
# 如果KL散度太大,提前停止更新
avg_kl = np.mean(approx_kl_divs)
if avg_kl > self.target_kl * 1.5:
print(f"Early stopping at epoch due to reaching max KL: {avg_kl:.4f}")
break
def train(self, env_name, num_episodes=1000, steps_per_epoch=2048, max_steps=1000000):
"""训练PPO智能体"""
# 创建环境
env = gym.make(env_name)
# 训练日志
scores = []
avg_scores = []
# 总步数计数
total_steps = 0
episode_count = 0
while total_steps < max_steps and episode_count < num_episodes:
# 收集轨迹数据
states, actions, old_log_probs, returns, advantages, episode_reward = self.collect_rollouts(env, steps_per_epoch)
total_steps += steps_per_epoch
episode_count += 1
# 更新策略
self.update_policy(states, actions, old_log_probs, returns, advantages)
# 记录和打印进度
scores.append(episode_reward)
avg_score = np.mean(scores[-100:]) if len(scores) >= 100 else np.mean(scores)
avg_scores.append(avg_score)
if episode_count % 10 == 0:
print(f"Episode {episode_count}/{num_episodes} | Total steps: {total_steps} | " \
f"Episode reward: {episode_reward:.2f} | Average score: {avg_score:.2f}")
return scores, avg_scores
def evaluate(self, env_name, num_episodes=10, render=False):
"""评估训练好的PPO智能体"""
# 创建环境
env = gym.make(env_name, render_mode='human' if render else None)
# 评估日志
scores = []
for _ in range(num_episodes):
state, _ = env.reset()
done = False
episode_reward = 0
while not done:
# 选择动作(确定性,取概率最高的动作)
with torch.no_grad():
state_tensor = torch.FloatTensor(state).unsqueeze(0).to(device)
action_probs, _ = self.policy(state_tensor)
action = torch.argmax(action_probs, dim=1).item()
# 执行动作
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
episode_reward += reward
state = next_state
if render:
env.render()
scores.append(episode_reward)
return np.mean(scores), np.std(scores)
# 示例用法
if __name__ == "__main__":
# 训练PPO智能体
env_name = "CartPole-v1"
# 创建PPO智能体
state_size = gym.make(env_name).observation_space.shape[0]
action_size = gym.make(env_name).action_space.n
ppo_agent = PPO(state_size, action_size, hidden_size=64, lr=3e-4, gamma=0.99,
gae_lambda=0.95, clip_ratio=0.2, target_kl=0.01, entropy_coef=0.01,
value_coef=0.5, max_grad_norm=0.5, update_epochs=4, batch_size=64)
# 训练智能体
scores, avg_scores = ppo_agent.train(env_name, num_episodes=100, steps_per_epoch=2048)
# 绘制训练曲线
plt.figure(figsize=(12, 6))
plt.plot(scores, alpha=0.6, label='Episode Reward')
plt.plot(avg_scores, label='Average Reward (100 episodes)')
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.title('PPO Training on CartPole-v1')
plt.legend()
plt.grid(True)
plt.savefig('ppo_training.png')
plt.show()
# 评估智能体
mean_score, std_score = ppo_agent.evaluate(env_name, num_episodes=10)
print(f"Evaluation: Mean Score = {mean_score:.2f} ± {std_score:.2f}")
# 可视化智能体行为(可选)
# ppo_agent.evaluate(env_name, num_episodes=3, render=True)
2.7 方差优化策略的对比分析
2.7.1 各种方差优化技术的理论对比
2.7.2 改进方差的数学原理
策略梯度估计的方差主要来源于奖励信号和采样过程。我们可以从数学上分析不同方法如何减少方差:
-
基线减法:如果定义 A ( s , a ) = Q ( s , a ) − b ( s ) A(s, a) = Q(s, a) - b(s) A(s,a)=Q(s,a)−b(s),我们可以证明只要基线 b ( s ) b(s) b(s) 只依赖于状态 s s s,引入基线不会改变梯度的期望,但会减小方差:
Var [ ∇ θ log π θ ( a ∣ s ) ⋅ ( Q ( s , a ) − b ( s ) ) ] ≤ Var [ ∇ θ log π θ ( a ∣ s ) ⋅ Q ( s , a ) ] \text{Var}[\nabla_\theta \log \pi_\theta(a|s) \cdot (Q(s,a) - b(s))] \leq \text{Var}[\nabla_\theta \log \pi_\theta(a|s) \cdot Q(s,a)] Var[∇θlogπθ(a∣s)⋅(Q(s,a)−b(s))]≤Var[∇θlogπθ(a∣s)⋅Q(s,a)]
当 b ( s ) = V π ( s ) b(s) = V^\pi(s) b(s)=Vπ(s) 时,方差减少最多。
-
时序差分学习:使用TD误差替代完整的折扣回报可以显著减少方差,因为它限制了估计的范围:
δ t = r t + γ V ( s t + 1 ) − V ( s t ) \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) δt=rt+γV(st+1)−V(st)
相比于回报 G t = ∑ k = 0 ∞ γ k r t + k G_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k} Gt=∑k=0∞γkrt+k,TD误差的方差通常小得多。
-
λ回报:GAE通过λ参数平衡偏差和方差:
A G A E ( γ , λ ) ( s t , a t ) = ∑ l = 0 ∞ ( γ λ ) l δ t + l A^{GAE(\gamma, \lambda)}(s_t, a_t) = \sum_{l=0}^{\infty} (\gamma \lambda)^l \delta_{t+l} AGAE(γ,λ)(st,at)=∑l=0∞(γλ)lδt+l
- λ = 0: 单步TD估计,低方差但高偏差
- λ = 1: 蒙特卡洛估计,无偏但高方差
- 0 < λ < 1: 两者之间的平衡
-
置信域约束:TRPO和PPO通过限制每次更新的"步长"来避免过大的策略变化,这间接减小了方差:
PPO的目标函数:
L C L I P ( θ ) = E t [ min ( r t ( θ ) A t , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A t ) ] L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min(r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t) \right] LCLIP(θ)=Et[min(rt(θ)At,clip(rt(θ),1−ϵ,1+ϵ)At)]
其中 r t ( θ ) = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} rt(θ)=πθold(at∣st)πθ(at∣st) 是重要性采样比率。通过剪切这个比率,PPO确保新策略不会与旧策略相差太远,从而提高训练稳定性。
-
熵正则化:添加策略的熵作为正则项,可以防止策略过早收敛到次优解,间接减少最终性能的方差:
L ( θ ) = E [ ∑ t log π θ ( a t ∣ s t ) A t ] + β H [ π θ ] L(\theta) = \mathbb{E}[\sum_t \log \pi_\theta(a_t|s_t) A_t] + \beta H[\pi_\theta] L(θ)=E[∑tlogπθ(at∣st)At]+βH[πθ]
其中 H [ π θ ] = − E a ∼ π θ [ log π θ ( a ∣ s ) ] H[\pi_\theta] = -\mathbb{E}_{a \sim \pi_\theta}[\log \pi_\theta(a|s)] H[πθ]=−Ea∼πθ[logπθ(a∣s)] 是策略的熵, β \beta β 是一个控制熵正则化强度的超参数。
2.7.3 实验性能对比分析
在不同环境中,各种方差优化技术的性能并不相同。下面是一些典型环境中的比较:
-
离散动作环境(如CartPole-v1):
- REINFORCE通常能够解决问题,但训练不稳定
- 带基线的REINFORCE收敛更快,性能更稳定
- A2C和PPO能够更快地收敛到更高的平均奖励
-
连续动作环境(如MuJoCo任务):
- 原始REINFORCE在这些任务上往往失败
- A2C在简单任务上表现尚可
- PPO和SAC(Soft Actor-Critic)在复杂任务上表现最佳
-
高维状态空间(如图像输入的Atari游戏):
- 所有算法都需要卷积神经网络处理输入
- A2C和PPO是这类任务的常用选择
- 带基线的REINFORCE很难在这些任务上收敛
2.8 实践中的选择与调优建议
根据不同的应用场景和要求,我们可以给出以下实用建议:
2.8.1 算法选择指南
| 场景 | 推荐算法 | 原因 |
|---|---|---|
| 入门学习 | REINFORCE、A2C | 实现简单,概念清晰 |
| 离散动作问题 | PPO | 稳定性好,超参数敏感度低 |
| 连续动作问题 | PPO、SAC | 样本效率高,性能稳定 |
| 稀疏奖励环境 | PPO+内在奖励 | 更好的探索能力 |
| 计算资源有限 | A2C | 计算开销较小 |
| 需要最高性能 | PPO、TD3 | 性能上限较高 |
2.8.2 超参数调优策略
策略梯度方法的超参数调优关键在于平衡探索和利用、控制更新步长:
-
学习率:
- 较大学习率(~1e-3)适合初期快速学习
- 较小学习率(~1e-4)适合后期精细调整
- 学习率衰减可以提高稳定性
-
折扣因子 γ:
- 较小的γ(~0.9)更关注近期奖励,适合短视野任务
- 较大的γ(~0.99)更看重长期回报,适合需要长远规划的任务
-
GAE的λ参数:
- 较小的λ(~0.9)减少方差但增加偏差
- 较大的λ(~0.99)减少偏差但增加方差
- 一般默认值0.95适用于大多数任务
-
PPO的剪切比率ε:
- 较小的ε(~0.1)更保守,训练更稳定但可能进展慢
- 较大的ε(~0.3)更激进,训练可能更快但风险更高
- 默认值0.2通常是个不错的平衡点
2.8.3 实际调优流程
在实际应用中,建议遵循以下调优流程:
- 从基线开始:使用已验证的默认参数设置开始(如PPO的推荐参数)
- 单变量调优:每次只调整一个参数,观察其影响
- 从关键参数开始:优先调整学习率、GAE的λ和剪切比率
- 使用网格搜索或贝叶斯优化:系统性地探索超参数空间
- 多次运行取平均:由于随机性,每组参数应运行多次取平均评估
2.9 策略梯度在复杂环境中的应用
策略梯度方法已在多个复杂环境中展现出强大能力,一些经典应用包括:
- 机器人控制:PPO成功应用于四足机器人的步态学习,实现了在复杂地形上的稳健行走
- 游戏AI:A3C和PPO在Atari游戏和星际争霸等复杂游戏中取得了超越人类水平的成绩
- 自动驾驶:模拟环境中的自动驾驶策略训练,处理各种复杂交通场景
- 自然语言处理:使用强化学习微调语言模型,优化特定目标(如减少有害输出)
这些成功应用的共同点是利用了各种方差优化技术,使训练过程更加稳定和高效。
2.10 总结
策略梯度方法从简单的REINFORCE发展到现在的PPO、SAC等先进算法,方差优化一直是核心研究方向。通过引入基线、优势函数、重要性采样剪切等技术,现代策略梯度算法大大提高了样本效率和训练稳定性。
清华大学全五版的《DeepSeek教程》完整的文档需要的朋友,关注我私信:deepseek 即可获得。
怎么样今天的内容还满意吗?再次感谢朋友们的观看,关注GZH:凡人的AI工具箱,回复666,送您价值199的AI大礼包。最后,祝您早日实现财务自由,还请给个赞,谢谢!