机器学习算法——PCA算法介绍以及Java实现
PCA算法
一、算法概述
主成分分析(PCA)是多元统计分析中用来分析数据的一种方法,PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
PCA方法最著名的应用应该是在人脸识别中特征提取及数据维,我们知道输入200*200大小的人脸图像,单单提取它的灰度值作为原始特征,则这个原始特征将达到40000维,这给后面分类器的处理将带来极大的难度。在这种情况下,我们必须对数据进行降维。
降维当然意味着信息的丢失,不过鉴于实际数据本身常常存在的相关性,我们可以想办法在降维的同时将信息的损失尽量降低。
例如某淘宝店铺的数据记录为(日期, 浏览量, 访客数, 下单数, 成交数, 成交金额),从经验我们可以知道,“浏览量”和“访客数”往往具有较强的相关关系,而“下单数”和“成交数”也具有较强的相关关系。这里我们非正式的使用“相关关系”这个词,可以直观理解为“当某一天这个店铺的浏览量较高(或较低)时,我们应该很大程度上认为这天的访客数也较高(或较低)”。后面的章节中我们会给出相关性的严格数学定义。
这种情况表明,如果我们删除浏览量或访客数其中一个指标,我们应该期待并不会丢失太多信息。因此我们可以删除一个,以降低机器学习算法的复杂度。所以,我们可以采用PCA进行降纬。
二、算法原理
1、数据准备
假设有M个样本,每个样本有N个特征,例如第i个(i=1,2,…,M)样本为:
![]()
则M个样本构成了M行N列的数值矩阵A。
2、数据归一化处理
通常做法是将每一维的数据都减去该维的均值,使每一维的均值都为0。
3、计算协方差矩阵
协方差是一种用来度量两个随机变量关系的统计量,其定义为:
![]()
M*N样本的协方差矩阵为:
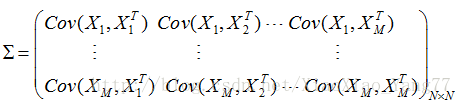
4、求出协方差矩阵的特征值及对应的特征向量
若AX=λX,则称λ是A的特征值,X是对应的特征向量。实际上可以这样理解:矩阵A作用在它的特征向量X上,仅仅使得X的长度发生了变化,缩放比例就是相应的特征值λ。
特别地,当A是对称矩阵时,A的奇异值等于A的特征值,存在正交矩阵Q(Q-1=QT),使得:
对A进行奇异值分解就能求出所有特征值和Q矩阵。
A∗Q=Q∗DA∗Q=Q∗D,D是由特征值组成的对角矩阵
由特征值和特征向量的定义知,Q的列向量就是A的特征向量。
5、将特征向量按对应的特征值大小从上往下按行排列成矩阵,取前k行组成矩阵P,P为k行n列矩阵
6、Y=AP’ 即为降维到k维后的数据,Y为M行k列矩阵
三、代码实现
PCA.class
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.Iterator;
import java.util.List;
import java.util.Map;
import java.util.Map.Entry;
import java.util.TreeMap;
import Jama.Matrix;
/*
* 算法步骤:
* 1)将原始数据按列组成n行m列矩阵X
* 2)特征中心化。即每一维的数据都减去该维的均值,使每一维的均值都为0
* 3)求出协方差矩阵
* 4)求出协方差矩阵的特征值及对应的特征向量
* 5)将特征向量按对应的特征值大小从上往下按行排列成矩阵,取前k行组成矩阵p
* 6)Y=PX 即为降维到k维后的数据
*/
public class PCA {
private static final double threshold = 0.95;// 特征值阈值
/**
*
* 使每个样本的均值为0
*
* @param primary
* 原始二维数组矩阵
* @return averageArray 中心化后的矩阵
*/
public double[][] changeAverageToZero(double[][] primary) {
int n = primary.length;
int m = primary[0].length;
double[] sum = new double[m];
double[] average = new double[m];
double[][] averageArray = new double[n][m];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum[i] += primary[j][i];
}
average[i] = sum[i] / n;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
averageArray[j][i] = primary[j][i] - average[i];
}
}
return averageArray;
}
/**
*
* 计算协方差矩阵
*
* @param matrix
* 中心化后的矩阵
* @return result 协方差矩阵
*/
public double[][] getVarianceMatrix(double[][] matrix) {
int n = matrix.length;// 行数
int m = matrix[0].length;// 列数
double[][] result = new double[m][m];// 协方差矩阵
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
double temp = 0;
for (int k = 0; k < n; k++) {
temp += matrix[k][i] * matrix[k][j];
}
result[i][j] = temp / (n - 1);
}
}
return result;
}
/**
* 求特征值矩阵
*
* @param matrix
* 协方差矩阵
* @return result 向量的特征值二维数组矩阵
*/
public double[][] getEigenvalueMatrix(double[][] matrix) {
Matrix A = new Matrix(matrix);
// 由特征值组成的对角矩阵,eig()获取特征值
// A.eig().getD().print(10, 6);
double[][] result = A.eig().getD().getArray();
return result;
}
/**
* 标准化矩阵(特征向量矩阵)
*
* @param matrix
* 特征值矩阵
* @return result 标准化后的二维数组矩阵
*/
public double[][] getEigenVectorMatrix(double[][] matrix) {
Matrix A = new Matrix(matrix);
// A.eig().getV().print(6, 2);
double[][] result = A.eig().getV().getArray();
return result;
}
/**
* 寻找主成分
*
* @param prinmaryArray
* 原始二维数组数组
* @param eigenvalue
* 特征值二维数组
* @param eigenVectors
* 特征向量二维数组
* @return principalMatrix 主成分矩阵
*/
public Matrix getPrincipalComponent(double[][] primaryArray,
double[][] eigenvalue, double[][] eigenVectors) {
Matrix A = new Matrix(eigenVectors);// 定义一个特征向量矩阵
double[][] tEigenVectors = A.transpose().getArray();// 特征向量转置
Mapdouble[]> principalMap = new HashMapdouble[]>();// key=主成分特征值,value=该特征值对应的特征向量
TreeMapdouble[]> eigenMap = new TreeMapdouble[]>(
Collections.reverseOrder());// key=特征值,value=对应的特征向量;初始化为翻转排序,使map按key值降序排列
double total = 0;// 存储特征值总和
int index = 0, n = eigenvalue.length;
double[] eigenvalueArray = new double[n];// 把特征值矩阵对角线上的元素放到数组eigenvalueArray里
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j)
eigenvalueArray[index] = eigenvalue[i][j];
}
index++;
}
for (int i = 0; i < tEigenVectors.length; i++) {
double[] value = new double[tEigenVectors[0].length];
value = tEigenVectors[i];
eigenMap.put(eigenvalueArray[i], value);
}
// 求特征总和
for (int i = 0; i < n; i++) {
total += eigenvalueArray[i];
}
// 选出前几个主成分
double temp = 0;
int principalComponentNum = 0;// 主成分数
List plist = new ArrayList();// 主成分特征值
for (double key : eigenMap.keySet()) {
if (temp / total <= threshold) {
temp += key;
plist.add(key);
principalComponentNum++;
}
}
System.out.println("\n" + "当前阈值: " + threshold);
System.out.println("取得的主成分数: " + principalComponentNum + "\n");
// 往主成分map里输入数据
for (int i = 0; i < plist.size(); i++) {
if (eigenMap.containsKey(plist.get(i))) {
principalMap.put(i, eigenMap.get(plist.get(i)));
}
}
// 把map里的值存到二维数组里
double[][] principalArray = new double[principalMap.size()][];
Iteratordouble[]>> it = principalMap.entrySet()
.iterator();
for (int i = 0; it.hasNext(); i++) {
principalArray[i] = it.next().getValue();
}
Matrix principalMatrix = new Matrix(principalArray);
return principalMatrix;
}
/**
* 矩阵相乘
*
* @param primary
* 原始二维数组
*
* @param matrix
* 主成分矩阵
*
* @return result 结果矩阵
*/
public Matrix getResult(double[][] primary, Matrix matrix) {
Matrix primaryMatrix = new Matrix(primary);
Matrix result = primaryMatrix.times(matrix.transpose());
return result;
}
} 主函数调用PCA:
import Jama.Matrix;
import java.io.FileWriter;
import java.io.IOException;
public class PCAMain {
public static void main(String[] args) throws IOException {
// TODO Auto-generated catch block
SelectData selectData = new SelectData();
PCA pca = new PCA();
//获得样本集
double[][] primaryArray = selectData.getdatas();
System.out.println("--------------------------------------------");
double[][] averageArray = pca.changeAverageToZero(primaryArray);
System.out.println("--------------------------------------------");
System.out.println("均值0化后的数据: ");
System.out.println(averageArray.length + "行,"
+ averageArray[0].length + "列");
System.out.println("---------------------------------------------");
System.out.println("协方差矩阵: ");
double[][] varMatrix = pca.getVarianceMatrix(averageArray);
System.out.println("--------------------------------------------");
System.out.println("特征值矩阵: ");
double[][] eigenvalueMatrix = pca.getEigenvalueMatrix(varMatrix);
System.out.println("--------------------------------------------");
System.out.println("特征向量矩阵: ");
double[][] eigenVectorMatrix = pca.getEigenVectorMatrix(varMatrix);
System.out.println("--------------------------------------------");
Matrix principalMatrix = pca.getPrincipalComponent(primaryArray, eigenvalueMatrix, eigenVectorMatrix);
System.out.println("主成分矩阵: ");
// principalMatrix.print(6, 3);
System.out.println("--------------------------------------------");
System.out.println("降维后的矩阵: ");
Matrix resultMatrix = pca.getResult(primaryArray, principalMatrix);
// resultMatrix.print(6, 3);
int c = resultMatrix.getColumnDimension(); //列数
int r = resultMatrix.getRowDimension();//行数
System.out.println(resultMatrix.getRowDimension() + "," + resultMatrix.getColumnDimension());
}
}