Depth-Aware Stereo Video Retargeting

深度感知的立体视频重定向

原文：Bing Li 等. CVPR 2018

摘要

  与传统视频重定向相比，立体视频重定向面临着新的挑战，因为立体视频包含突出物体的深度信息，并且还随物体的运动而改变。本文提出了一个深度感知的立体视频重定向方法，是通过添加深度保真约束实现的。本方法通过重建 3D 场景获得显著物体的深度信息。我们把它考虑为一个约束优化问题，它的总损失函数包括显著物体的形状，时序性和深度畸变。因此，本方法可以同时保证上述三方面的保真度。实验证明深度感知的重定向方法达到了更高的重定向质量，提供了更好的用户体验。

1 引言

  3D 视频内容和显示技术日趋成熟，它们能为用户提供真实世界的视觉体验。顺应趋势发展，许多公司正在制造不同尺寸的 3D 显示设备以适应不同的应用场景包括剧场，电视和电脑。此外，虚拟/增强现实设备 (例如 Google Cardboard 和 Oculus Rift) 也用立体视频创造有沉浸感的环境。一个重要的任务是让相同的立体内容自动地适配到不同尺寸不同宽高比的显示设备上，叫做 resizing 技术。

  与 2D 视频重定向相比，立体视频重定向面临着新的挑战，因为立体视频包含突出物体的深度信息，并且还随物体的运动而改变。当物体沿着深度方向运动时尤其明显，见图 1，造成很糟糕的 3D 观看体验。通常来讲，影响人 3D 观看体验的有两个关键因素，一个是每一个正确的静态帧的深度信息，另一个是正确的多帧间的深度变化。前者决定了 3D 物体到屏幕的距离，而后者指示了运动方向和速度。为了获得令人满意的 3D 观看体验，我们设计的立体视频重定向方法需要在传统 2D 保留形状和时间相干性的基础上，同时考虑上述两个因素。

  需要说明的是，大多数现有的视频重定向方法不包含深度保真约束。例如，resize 立体视频时广泛采用的均匀缩放的方法，分别对立体视频的左右 2D 视频进行上或下采样，显著物体的深度可能发生畸变。图 1 对比了均匀缩放和我们提出的深度感知重定向策略。均匀缩放只缩小了女孩的尺寸，但是没有正确地捕捉到她在深度方向上的运动，感知到的深度变化相对较小。显然，立体视频重定向问题不能用传统 2D 视频重定向方法解决，因为它们不会综合分析左右图，没有保留住显著物体的深度信息，见图 2。

  在本文中，我们提出了一种深度感知的立体视频重定向方法，这种方法保留了原始立体视频中的深度信息，实现了高质量的重定向。我们的方法在总损失函数中引入了深度信息及其偏差，又采用了 grid warping 策略来改进优化框架。据我们所知，这是首个考虑深度保留约束的立体视频重定向研究，我们提出的约束简单且应用灵活。一旦检测到了显著物体，算法将会尽可能如实地保留它们的深度信息。这提高了用户观看 3D 重定向视频的体验。实验结果也表明了本方面的优越性能。

图 1：深度感知重定向方法的优势。$(a)$-$(c)$ 的左侧是 $t_1$ 和 $t_2$ 时刻的 3D 场景，右侧是场景中前景物体的时间变化轨迹。$(b)$ 均匀缩放仅仅缩小了女孩的尺寸但没有正确捕捉到她在深度方向上的运动，感知到的深度变化相对较小。相比之下，$(c)$ 深度感知的重定向方法既保留了女孩的形状又保留了深度信息，感知到的深度变化接近原图 $(a)$。

图 2：$t_1$ 和 $t_2$ 时刻的前景物体 (女孩) 。$(a)$ 和 $(b)$ 的上图是左视点，下图是右视点。$(c)$ 中屏幕上的红色和绿色点分别表示女孩在左右 2D 帧中的 $x$ 坐标。基于 $x$ 坐标的差异，我们可以确定女孩的深度，她从 $t_1$ 到 $t_2$ 朝相机方向移动了。然而女孩在左视点 (或右视点) 上水平移动，所以传统的视频重定向算法不能恢复立体视频中的深度变化信息。

2 相关工作

2D 视频重定向 内容感知的重定向方法可以被分为离散的和连续的两类。2D 视频重定向方面有许多离散的方法被提出，基于裁剪的方法从每个 2D 帧中裁剪出一个矩形区域，线裁剪 方法反复地移除或添加裁剪线。连续的方法把视频帧划分成像素或区域，根据重要程度图来 warp。离散的方法容易引入肉眼可见的结构性物体的畸变。连续的方法得益于它们连续性 warping 的机理，往往能更好地保留物体的形状。根据时间约束中利用的信息，2D 视频重定向方法可以分为局部方法和全局方法。局部方法缩放时考虑与它相邻的若干帧。全局方法采用整个视频的时间信息，因此得到比局部方法更好的时间上的形状一致性。

立体图像重定向 Basha 等和 Shen 等把线裁剪方法扩展到立体图片重定向上来，通过在立体图片对儿上迭代地移除一对裁剪线。几个连续的方法通过添加额外的深度保留约束，把基于 warp 的 2D 图像重定向方法扩展到立体图像对儿上。这些方法试图通过保持一组稀疏的对应来保留全图的深度。这个想法和深度编辑方法很相似。还有方法提出重映射深度。Li 等人在 grid warping 上添加了有效的深度保留约束，取得更好的深度保留性能。

立体视频重定向 相对于立体图像重定向，关于立体视频的研究少很多。因为形状和深度两方面在时间相干性上的额外要求使得问题更加复杂。Kopf 等把立体视频看成两个独立的 2D 视频，用 2D 视频重定向方法来缩放立体视频。对于立体视频 (尤其当显著物体或者它们的移动占据了一帧的大部分时) ，Lin 等人提出将裁剪和基于网格的 2D 视频重定向相结合。然而，由于上述方法没有明确地考虑 3D 物体是深度信息和时间动力学，它们往往导致严重的深度瑕疵。

3 深度感知的立体视频重定向

3.1 问题公式化

  立体视频重定向是将立体视频适配到目标显示尺寸，试图使用户的 3D 观看体验最佳。对于左右视点混合形成的 3D 场景，场景中的 3D 物体有两个关键属性——形状和深度。由于相机运动和物体运动，这两个属性随时间变化。在现有的文献中，内容感知的 2D 视频重定向方法确保形状信息在空间和时间上的保真。就是说，每一帧中 3D 物体的形状都被保留，多帧上的形状也前后一致。然而，随时间变化的深度属性往往被忽略了。现有方法分别保留左右视点的可视内容，与之不同，我们的解决方案尽可能地以原始形式保留形状和深度信息以及它们的时间动力学。

  3D 场景中的 3D 物体有不同的深度。当人的双眼注视在一个物体上时，如图 3 中的点 P，视线交叉在这个物体上，两眼的视界也形成了。在这个物体前面或后面的物体都变得模糊。因为在观看立体视频时，人眼视觉系统 (HVS) 一次只注视一个物体，其他物体都模糊了，所以它们的深度可以在一定程度上改变，只要基本不影响观看体验。此外，非显著物体和背景的时域深度变化是受物体和相机的运动影响的，需要在多帧上一致地改变它们的深度，否则常常会导致错误的运动方向 (例如非显著物体出或入屏幕的混乱)。双目视差-聚焦模糊冲突 和过长的读取时间也可能导致深度不连续和无法感知深度。受上面提到的 HVS 的特性启发，我们提出了一种深度感知的重定向解决方案，不仅仅保留显著 3D 物体的形状和深度，还可以前后一致地缩放整个 3D 场景。

图 3：人类视觉系统中聚焦点之外的物体会变得模糊。

  为了得到高质量的立体视频重定向算法，我们构建了如下最小化问题：

$$minE=min(E^S+{\lambda }^S\cdot E^T+{\lambda }^D\cdot E^D)\text{\hspace{1em}(1)}$$

其中 E 是总畸变，$E^S,E^T,E^D$ 分别表示空间形状不相干，时域形状不相干和显著物体的 3D 深度信息损失，即形状畸变，时域畸变和深度畸变。${\lambda }^S$ 和 ${\lambda }^D$ 是权重。深度畸变 $E^D$ 的来源将在 3.2 节中详细阐述，$E^S$ 和 $E^T$ 见 3.3 节。

  基于网格的 warping 已经被证明是一个重定向图像和视频的有效手段。它把每一帧划分成网格，将寻找最优重定向了立体视频的问题转化成搜寻最优的变形的网格集合，最小化公式 (1) 中的总畸变 E。对于立体视频，这个寻优过程涉及大量的参数，需要消耗大量的内存和时间。为了降低复杂程度，我们采取轴对齐的 warping 策略，使用网格的宽和高作为参数来控制变形，要求每一列和每一行的网格分别具有相同的宽和高。与以网格顶点为参数的方法相比，参数数量显著减少。我们使用 $w_k^{z,t}$ 和 $h_i^{z,t}$ 分别表示网格的宽和高，$g_k^{z,t}$ 表示原始网格的边长，寻找最优的 ${\tilde{w}}_k^{z,t}$ 和 ${\tilde{h}}_k^{z,t}$ 使得总畸变最小。

图 4：稠密 3D 点表示的 3D 物体“熊猫”：(a) $s^{t_1}$ 和 $s^{t_2}$ 两个场景中的 3D 熊猫；(b) 离散成 3D 点的 3D 熊猫，3D 点用黄色圆表示，黄色线表示两个场景中的对应关系；(c)一个 3D 点是由左右图中对应的两个 2D 点表示的，黄色圈表示 2D 点。

3.2 深度畸变

  在本节中，我们将重点关注深度畸变 $E^D$ ，$E^S$ 和 $E^T$ 将在第 3.3 节中讨论。深度畸变是用来保持立体视频中的显著物体的深度信息的。独立帧和多帧间的时序性深度保真我们都会考虑。

  一个 3D 物体的不同部分可能会在深度上做不同方向的运动。图 4 (a) 展示了一个 3D 熊猫的例子，左右两图分别是 $s^{t_1}$ 和 $s^{t_2}$ 两个场景。很显然仅仅在物体尺度上表现深度变化是不够的。我们需要将物体离散化成一些有代表性的 3D 点，像图 4 (b) 中那样检查它们的深度变化轨迹。对于一个被分解为 N 个点的 3D 物体，$E^D$ 即为 N 个深度变化轨迹的加权和：

$$E^D=\sum _i^n{s}_i\cdot E_i^D\text{\hspace{1em}(2)}$$

其中 $E_i^D$ 是第 $i$ 个点的深度变化轨迹的畸变，$s_i$ 是相应的权重，用于表示第 $i$ 个深度变化轨迹的重要程度。$s_i$ 定义为第 $i$ 个深度变化轨迹上的 3D 点的显著性值的平均，显著性值的定义见 3.3 节。

  用 $d^{i,t}$ 和 ${\tilde{d}}^{i,t}$ 分别表示第 $i$ 个点在原始和重定向视频中的第 $t$ 帧的深度值，${\mathbf{d}}^i=\{d^{i,t}\}$ 和 $\widetilde{{\mathbf{d}}^i}=\{{\tilde{d}}^{i,t}\}$ 分别表示第 $i$ 个点在原始和重定向视频中的多帧上的深度变化轨迹。每个深度变化轨迹都被假定为连续并一阶可微的。这样，第 $i$ 个深度变化轨迹的畸变就被定义为：

$$E_i^D=\sum \left((\Delta d^{i,t}{)}^2+(\Delta \frac{\partial {\mathbf{d}}^i}{\partial t}{|}_t{)}^2\right)\text{\hspace{1em}(3)}$$

其中第一项对应空间上的深度畸变：

$$\Delta d^{i,t}=d^{i,t}-{\tilde{d}}^{i,t}\text{\hspace{1em}(4)}$$

第二项对应轨迹 ${\mathbf{d}}^i$ 的第 $t$ 帧在时序上的深度变化畸变：

$$\Delta \frac{\partial {\mathbf{d}}^i}{\partial t}{|}_t=\frac{\partial {\mathbf{d}}^i}{\partial t}{|}_t-\frac{\partial \widetilde{{\mathbf{d}}^i}}{\partial t}{|}_t\text{\hspace{1em}(5)}$$

我们在公式 (5) 中采取如下的近似计算：

$$\begin{gathered} \frac{\partial {\mathbf{d}}^i}{\partial t}{|}_t=d^{i,t}-d^{i,t+1} \\ \frac{\partial \widetilde{{\mathbf{d}}^i}}{\partial t}{|}_t={\tilde{d}}^{i,t}-{\tilde{d}}^{i,t+1} \end{gathered}$$

  在第 3.1 节中提到过，公式 (3) 中的畸变 $E_i^D$ 应该被表示成网格的宽和高的形式来做最优化。一个 3D 点是由左右图中两个合适的对应点形成的，见图 4 (c)。众所周知，一个 3D 点的深度，$d_i^t$，会随着 x 轴上差异的增大而增大。因此，可以 $E_i^D$ 可以表示成网格的宽的函数，也就是说，只要将水平差异和网格宽度联系起来，就可以将 $E_i^D$ 表达成 $E_i^D(w^{z,t},w^{\tilde{z},t})$ 的形式。

  为了得到公式 (2) 中的 $E_i^D$，一个可能的方式是检测每个立体对儿上的所有的 3D 点，用差异估计算法计算 $d^{i,t}$。之后，我们通过运动估计算法匹配多帧上对应的 3D 点，以便计算 $\partial d^{i,t}/\partial t$。这个方法依赖于稠密运动估计和差异估计。然而，从稠密点估计 $E^D$ 不仅消耗巨大的内存，也使公式 (1) 变成了一个庞大的模型，带来高昂的计算代价。除此之外，对于包含大量无定形区域的视频帧，运动和差异估计可能不可靠，由此构造了错误的损失函数，大幅度降低重定向的立体视频的视觉效果。

  与之不同，我们打算基于少量的可靠的 3D 控制点来估计 $E_i^D$。可以直接用一些稀疏的深度轨迹来表示 $E_i^D$，但是这样很容易受严重的运动估计错误影响，产生不准确的深度跟踪轨迹，进而影响最终结果。为了解决这一问题，我们采取了一种类似样条插值的策略，通过网格上的一些控制点来逼近一维曲线和二维表面。这涉及两个任务。第一，我们使用少量的控制点来构建空间 (左/右) 和时间域的对应关系。第二，我们使用 grid warping 技术来近似深度图及其时间动力学，以便建立稠密 3D 点的对应关系，避免跟踪错误导致的深度畸变。

  结合公式 (2) 和 (3)，我们可以将 $E^D$ 表示成

$$E^D=\tau \cdot (E^C+E^W),\tau \equiv \underset{i}{\min }{s}_i\text{\hspace{1em}(6)}$$

其中

$$E^C=\sum _{i\in \mathbf{C}}\sum _t(\frac{s_i-\tau }{\tau }\cdot (\Delta {\tilde{d}}^{i,t}{)}^2+\frac{s^i}{\tau }\cdot (\Delta \frac{\partial {\tilde{d}}^i}{\partial t}{)}^2)$$

表示被选中的一个控制点的集合 $\mathbf{C}$ 的深度畸变，

$$E^W=\sum _i\sum _t(\Delta {\tilde{d}}^{i,t}{)}^2$$

表示空间和时间上的 grid warping 畸变。

  首先考虑 $E^C$，有几种方式从 3D 点的稠密集合中选择可靠的控制点。例如，我们可以移除无明显结构区域的 3D 点，提取 SIFT 和 SURF 这样的局部特征来匹配两个视点中的典型点。根据前人的经验，我们选择了 SIFT 特征。需要注意的是，在某些帧上，被追踪的 SIFT 点可能由于显著的运动、模糊和遮挡而数量过少。我们处理这个问题是方式是重新初始化新的轨迹，或者跳过相应帧，利用插值生成重定向结果。

  我们采用 grid warping 策略，用 $E^W$ 表示每一帧上的空间深度畸变，通过交换 $t$ 和 $i$ 的求和顺序，也就是说

$$E^W=\sum _i\sum _t(\Delta {\tilde{d}}^{i,t}{)}^2=\sum _t\sum _i(\Delta {\tilde{d}}^{i,t}{)}^2\cdot {\Gamma }_{i,t}\text{\hspace{1em}(7)}$$

其中 ${\Gamma }_{i,t}$ 指示轨迹 ${\mathbf{d}}^i$ 是否出现在场景 $S^t$ 中。${\sum }_i(\Delta {\tilde{d}}^{i,t}{)}^2\cdot {\Gamma }_{i,t}$ 是一副左右帧 ($I^{L,t}$ 和 $I^{R,t}$) 上所有 3D 点总的深度畸变。令

$$\sum _i(\Delta {\tilde{d}}^{i,t}{)}^2\cdot {\Gamma }_{i,t}=0$$

我们得到了如下两个 warping 约束：

$$\{\begin{array}{ll}\sum _{q_k^{z,t}\in {\bar{r}}_j^z}{\tilde{w}}_k^{z,t}=\sum _{q_k^{z,t}\in {\bar{r}}_j^z}{w}_k^{z,t},& \forall {\bar{r}}_j^z\in \overline{{\rm Y}}\\ {\tilde{w}}_k^{L,t}-w_k^{L,t}={\tilde{w}}_k^{R,t}-w_k^{R,t},& \forall g_k^{z,t}\in r_j^z,\forall r_j^z\in {\rm Y}\end{array}\text{\hspace{1em}(8)}$$

其中 $\overline{{\rm Y}}$ 和 ${\rm Y}$ 分别表示非配对区域 ${\bar{r}}_j^z$ 的集合和配对区域 $r_j^z$ 的集合。然而，直接在 $E^W$ 中使用公式 (8) 的条件过于严格了，因为无空间深度畸变的要求往往和 3.3 节中提到的空间域和时间域上的形状保留约束相矛盾。因此我们放弃公式 (8) 的严格形式，采用对应的 soft 形式，即 square difference。最终我们得到了如下的 grid warping 畸变：

$$E^W=\sum _t\left(\sum _{q_k^z\in {\bar{r}}_j^z}{\varpi }_k({\tilde{w}}_k^{z,t}-w_k^{z,t}{)}^2+\sum _{r_j^z\in {\rm Y}}\sum _{q_k^z\in r_j^z}({\tilde{w}}_k^{L,t}-w_k^{L,t}-({\tilde{w}}_k^{R,t}-w_k^{R,t}){)}^2\right)\text{\hspace{1em}(9)}$$

3.3 空间-时间域形状畸变

  为了保留显著物体的形状，我们将立体视频的形状畸变定义为所有网格的总形状畸变。因为重定向的网格仍然是长方形的，网格 $g_k^{z,t}$ 的形状畸变可以按照纵横比的差异简单衡量：

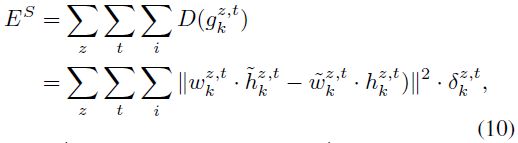
其中 $s_k^{z,t}$ 是 $g_k^{z,t}$ 的显著性值，是对 $g_k^{z,t}$ 中所有像素的显著性值求平均得到的。像素显著性值 ${\delta }_k^{z,t}$ 是将基于图像的显著性和基于差异的显著性加权求和得到的。

  为了保留 3D 物体的时序形状一致性，我们需要前后一致地缩放左右视点上的每个对应物体。给定 $I^{z,t}$ 中的 $g_k^{z,t}$，我们可以利用光流估计将其和 $I^{z,t^{\prime }}$ 中的 $g_j^{z,t}$ 匹配起来。然后，我们将时域网格畸变在水平和竖直方向分别相加：

其中 $A(k)$ 是与 $g_k^{z,t}$ 匹配的网格的集合。

4 实验

实施 我们最小化公式 (1) 中的目标函数，搜寻服从边界和空间相邻约束的最优的网格集合。这是一个二次优化问题，可以利用 active-set 方法求解。与现有的重定向方法类似，我们的方法包含一些可调节的参数，例如 ${\lambda }^S$ 和 ${\lambda }^D$，是形状和深度损失函数的权重。我们在实验中恒定设置 ${\lambda }^D=10^5,{\lambda }^S=10^3$。

性能比较 因为现有的立体视频重定向方法很少，我们将我们的方法与两种现有方法比较：均匀缩放 (US) 和恒定体积变形 (CVW)。CVW 在基于 warping 的立体视频重定向中 state-of-the-art，并且与我们的研究关联最大。我们在不同的测试视频上测试这三种方法，大多数来自于 CVW 使用的数据集。这些测试视频中包含多种运动和深度范围很大、变化明显的显著物体，带来重定向上的挑战。我们保持视频的高度不变，将宽度缩小到一半。因为 CVW 数据集中的显著性物体通常占据一帧中的很大区域 (超过 50%)，如图 5 所示，所以不能简单地裁剪掉不重要区域，而需要结合裁剪和 warping。CVW 和我们的方法都采取了这种策略。一个好的立体视频重定向方法应该既保留显著 3D 物体的形状和深度属性，又确保形状和深度的时间连续性。受篇幅所限，我们仅仅以每个视频中的两帧来展示重定向结果，在补充材料中给出了更多结果。注意，时间域深度保真效果可以通过对应的差异图来评估，图 5 中红色表示最小的负差异，蓝色表示最大的正差异。

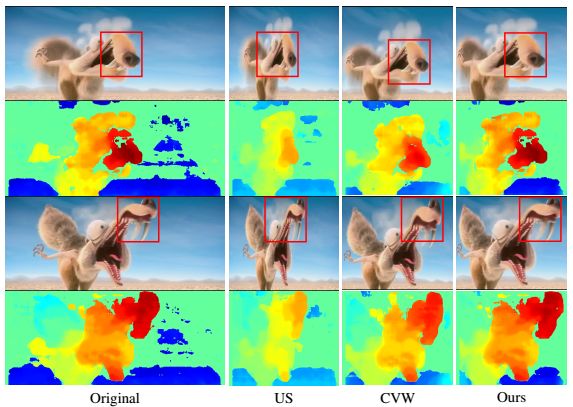
图 5：两个特写镜头的左图和差异图，来自电影冰川时代 4。左图中用红色方块标出了深度值高的区域。

  图 5 展示了特写镜头的重定向结果。这个视频的背景是静态的，而前景物体在时间空间域上有很强的深度。松鼠在镜头前面，沿深度方向冲出来。在时间连续性上，所有三个方法都表现优异。至于空间上，US 因为根本不考虑视频内容，将松鼠的形状缩小了。CVW 因为包含了形状损失函数因而比 US 更好地保留了形状。然而，CVW 改变了松鼠鼻子的形状。在这三个方法中，我们的方法给出了最佳的形状保真度。在空间和时间上的深度保真方面，US 减小了每一帧中松鼠的深度和帧间的深度变化，因为它不考虑深度信息。CVW 也使每帧的深度值发生了畸变并且减小的松鼠在深度方向上的运动范围。与之不同，我们是方法由于精心设计的深度损失函数，很好地保留了松鼠的空间-时间深度信息。

  图 6 展示了一个镜头移动缓慢的远景镜头。大多数远景镜头的前景物体的深度不像特写镜头中那样强烈。然而背景是深度值很大以增大整个 3D 场景到镜头的距离。通过保留深度信息，我们的方法可以保留这样的观看体验。而 US 和 CVW 减少了深度值，导致用户对整个 3D 场景的深度感知变弱。

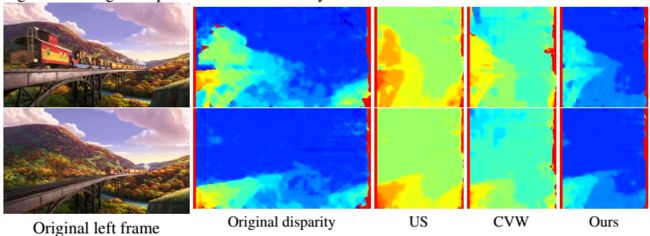
图 6：三个方法在两个远景镜头上的差异图对比，来自电影马达加斯加 3。

  除了 CVW 数据集，我们右在更有挑战性的视频上进行了测试，如图 7 和 8 所示。这些视频包含多个前景物体和相对复杂的背景，深度值很强烈。此外，这些视频中包含显著的相机运动和物体运动，导致明显的时序上的深度变化，使得深度保真非常具有挑战性。因为我们没办法得到 CVW 在这些视频上的测试结果，所以我们实现了 CVW 中提出的约束条件来建立了一个基准，叫做 sCVW。结果表明，我们的方法可以很好地保留显著物体的空间-时间深度，而 US 和 sCVW 有所损失，因为它们缺少有效的深度保真约束。

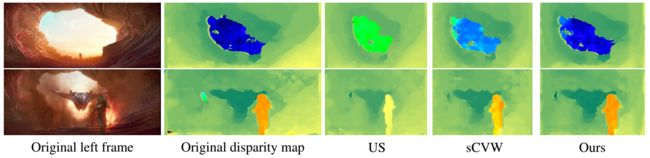
图 7：三个方法的差异图对比，来自电影银河护卫队 2

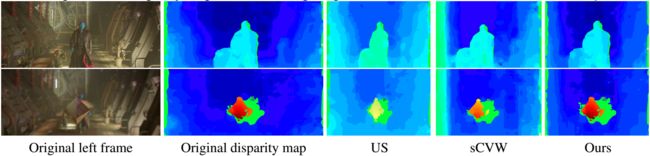
图 8：三个方法的差异图对比，来自电影银河护卫队 2

  我们也与有代表性的 2D 图像或视频重定向方法做了比较，使用 VOC 中的图片。图 10 显示我们的方法相比 SLR 和 SC，能够更好地保留物体的形状，虽然物体的尺寸缩小了。

定量分析 据我们所知，对于重定向立体视频的空间-时间域深度保真，目前还没有一个被广泛采用的衡量指标。我们提出了一个客观的衡量标准叫做差异畸变率 (DDr)。这个指标计算重定向视频和原始视频间 3D 点的平均差异偏差比，按如下公式归一化：

其中 $d_k^{z,t}$ 是 $g_k^{z,t}$ 的深度，$N^v$ 是 3D 点的总数，$|d_{max}|$ 是原始视频中差异的最大量级。如图 9 所示，与 US 和 CVW 相比，我们的方法取得了最低的深度畸变。

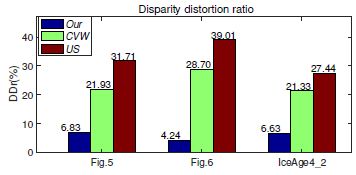
图 9：用图 5 和图 6 中的视频以及 IceAge4_2 进行深度畸变评估，IceAge4_2 是电影冰川时代 4中的一个特写镜头。

图 10：与 2D 重定向方法的对比

用户测试 进行主观评估测试时，我们用一个 22 英尺的 3D 显示器，英伟达主动快门眼镜和英伟达 GeForce 3D 视觉方案。我们邀请了 10 名受试者参加测试，包含 7 名男性，3 名女性。其中有 2 名受试者是 3D 感知领域的专家，其余的不是。我们在 5 个立体视频上与 US 和 CVW 作比较，将原始视频放在中间，在其左右随机放两个重定向的视频。受试者可以暂停、快进和快退，然后回答下面的问题：哪一个重定向视频更接近原始视频？

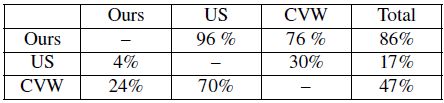
  最终，我们收集到 $3\times 5\times 10=150$ 个回答，每个方法被成对比较了 $2\times 5\times 10=100$ 次。表 1 展示了回答的百分比。76% (译者注：原文是85%？？) 的参与者支持我们的方法相比于 CVW，96%的参与者支持我们的方法相比于 US。这一结果清晰地表明了我们的方法在深度保真方面相对于 US 和 CVW 的优越性。主要原因是大多数受试者特别注意有强烈深度值的区域 (尤其是移动出屏的物体)，这使得这些区域的深度畸变更容易被注意到。因为我们的方法更好地保留了深度信息，所以通常可以带来更好的 3D 观看体验。

表 1：三种方法在主观测试中胜出的百分比

讨论 我们的方法可以轻易地与现有的重定向框架结合。例如，我们给出了我们的方法与 per-vertex 优化集成后的结果。Per-vertex 优化已经在几个 2D 图像或视频重定向方法中被采用。如图 11 所示，per-vertex 优化经常引入形状畸变，因为它 warping 的自由度很高，不过由于深度保留能量函数，重定向结果很好地保留了深度。然而，per-vertex 优化的复杂度要远远高于轴向对齐的 warping。具体地讲，per-vertex 优化的复杂度是 $4\cdot N_t\cdot (N_c\times N_r)$ 的形式，其中 $N_t$ 是总帧数，$N_c$ 和 $N_r$ 分别是一帧中网格的列数和行数。而轴向对齐的 warping 的变量数量为 $2\cdot N_t\cdot (N_c+N_r)$。

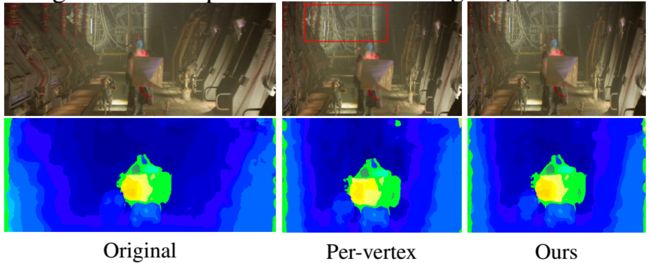
图 11：我们的方法与 per-vertex 优化的集成。上面是左图，下面是差异图。

  此外，在实际应用中还有另一个重要问题：对于立体视频，一些显示和观看情景可能会产生不合适的感知深度，引起观看者的不适。为了解决这一问题，我们的方法和一个深度重定向结合，先根据给定的观看情景构建舒适的感知深度图，然后获得目标差异图并且改善公式 (3)，这样立体视频的差异就被重新映射到需要的目标差异值上了。

5 总结

  提出了一个新方法在立体视频重定向过程中保留深度效果。导出了一个考虑深度保留需求的损失函数，并与总损失函数相结合。构建并解决了一个基于网格变形的优化问题，给出了一个有效的立体视频重定向方法，可以保留显著区域的深度，前后一致地转化其他非显著区域，并同时实现空间-时间域上的形状连续性。提出的深度感知重定向方法很灵活，允许与用户交互来强调感兴趣的区域。我们的方法实施简单，设计一个合适的界面，就可以容易地结合到编辑 VR 或立体视频内容的工具箱。