图像形成 (1) 图像的表达和针孔成像模型
文章目录
- 图像形成 (1) 图像的表达和针孔成像模型
- 前言
- 图像的表示
- 透镜,曲面和光源
- 透镜成像
- 薄透镜数学模型
- 针孔成像
- 博文内容总结
图像形成 (1) 图像的表达和针孔成像模型
前言
本次博文系列介绍图像形成过程。 在广义的意义上,视觉是图像形成的逆问题:后者研究物体如何提高图像,而前者试图使用图像来恢复空间物体的描述。 因此,设计视觉算法需要首先开发合适的图像形成模型。 在这种情况下合适并不一定意味着物理上准确:在建模图像形成中的抽象水平和复杂性必须与物理约束和数学简单性折衷(权衡),以便产生可管理的模型(即,可以容易地求逆的模型)。
几个世纪以来,图像形成的研究一直处于艺术再现和构图领域,而不是数学和工程领域。包括用于将三维世界投影到平面(例如,画布)上的各种模型的图像形成的几何的基本理解,隐含在来自所有古代文明的各种形式的视觉艺术中。然而,将图像形成几何形式化为数学模型的根源可以追溯到公元前6世纪欧几里德的工作。
正确的透视投影的例子在公元前一世纪时Pompeii城的惊人壁画和镶嵌画中可见,如下图所示。

在Pompeii城公元前一世纪的壁画 。 在绘画中可以看到更多(左)或更少(右)正确的透视投影。 这种技能在中世纪时期就已经消失了,直到十五世纪之后,在文艺复兴早期,它才重新出现在绘画中。
不幸的是,随着罗马帝国的衰落,这些技能似乎已经失去了,并且在14世纪后期,正确的透视投影花了一千多年才重新统治绘画。文艺复兴时期的早期画家开发了用于确定三维景观透视投影的系统方法。关于观点的第一篇论文"Della pittura"由Leon Battista Alberti发表,他强调了“眼睛对世界的看法”,并正确地捕捉了投影过程的几何形状。文艺复兴恰逢第一次尝试将透视投影的概念形式化并运用和分析。
早期的透视规则形式化的尝试是来自建筑和工程领域的艺术家,例如Alberti和Brunelleschi,但这并非巧合。然而,几何学只是图像形成过程的一部分:为了形成图像,我们不仅需要决定在哪里绘制什么,而且还要决定分配给图像上任何特定位置的颜色或灰度值。
光与物质的相互作用是莱昂纳多达芬奇在16世纪的研究的核心,他对透视,阴影,色彩甚至立体视觉的见解在他的笔记本中充满活力地表达出来。文艺复兴时期的画家,如卡拉瓦乔(Caravaggio)或拉斐尔(Raphael),在渲染光线和色彩方面表现出相当复杂的技艺,至今仍然非常引人注目。
Raphael, The School of Athens (1509)
博文系列中,博主会对图像形成几何的简单模型进行精确描述,然后描述其光度测量的相当粗糙的模型,即光与几何体如何相互作用如何形成图像,来追寻图像形成模型的历史发展。 我们将使用足够强的假设来将图像形成过程简化为完全几何模型,然后我们可以进行分析研究。
图像的表示
图像是二维亮度矩阵。 换句话说,它是一个映射 I \rm I I,定义在二维表面的紧凑区域 Ω \Omega Ω上,取正值的值。 例如,在相机的情况下, Ω \Omega Ω是由照相介质(或CCD传感器)占据的平面矩形区域,因此我们具有:
I : Ω ⊂ R 2 → R + ; ( x , y ) ↦ I ( x , y ) I:\Omega\sub \mathbb{R}^2 \rightarrow \mathbb{R}_+;(x,y)\mapsto I(x,y) I:Ω⊂R2→R+;(x,y)↦I(x,y)
例如,这样的图像可以表示为 I I I 的图形,如图1所示。
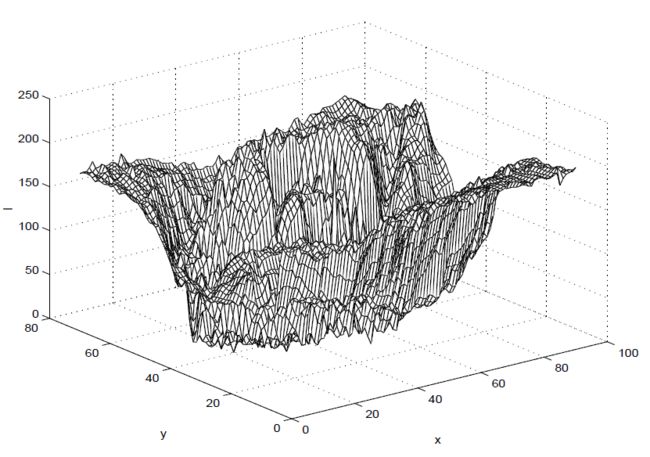
图1。 I I I 表示为二维表面的图像
在数字图像的情况下,定义域 Ω \Omega Ω和值域 R + \mathbb{R}_+ R+都是离散的。 例如, Ω = [ 1 , 640 ] × [ 1 , 480 ] ⊂ Z 2 \Omega =[1,640]\times [1,480] \sub \mathbb{Z}^2 Ω=[1,640]×[1,480]⊂Z2和 R + \mathbb{R}_+ R+近似于区间 [ 0 , 255 ] ⊂ Z + [0,255]\sub \mathbb{Z}_+ [0,255]⊂Z+。 这样的图像可以表示为下表中的数字数组。

表1。图像 I I I 表示为整数的二维表。
I I I中的值取决于所观察场景的物理属性,例如其形状,材料反射特性和光源分布。
尽管图1和表1似乎并不能很好地表明它们描绘的场景的属性,但这就是它们在计算机中的表现方式。
图片是一个场景 - 与真实场景不同 - 在成像传感器(在这种情况下是眼睛)上产生与原始场景相同的图像。 这个场景图像被称为是“受控的错觉”:它们是与真实场景不同的场景(它们是扁平的),是在眼睛中产生与原始场景相同的图像。图1和表1都是描述图2的一种表示,但后者看起来更具信息性,但它只是一个不同的表示,并包含完全相同的信息。

图2。数字数组 I I I 表示的图像。
透镜,曲面和光源
为了描述图像形成过程,我们必须在 Ω \Omega Ω中每个点 ( x , y ) (x,y) (x,y)处指定 I ( x , y ) I(x,y) I(x,y)的值。 这样的值 I ( x , y ) I(x,y) I(x,y)通常被称为图像亮度(image brightness)或正规称为辐照度(irradiance)。 它具有每单位面积的功率单位( W a t t s / m 2 Watts/m^2 Watts/m2),并描述落在成像传感器的patch块上的能量。 坐标点 ( x , y ) (x,y) (x,y)处的辐照度通常通过在时间上(例如相机中的快门间隔,或CCD中的积分时间)和空间上获得。 在 ( x , y ) (x,y) (x,y)处有助于辐照度的空间区域取决于成像装置的几何形状和光学,并且决不是微不足道的。 我们将采用通用的简化假设来近似它。 一旦确定了空间区域,它所贡献的能量取决于场景的几何形状和材料以及光源的分布。
在详细介绍如何构建图像形成模型之前,我们暂停考虑一类特定的对象,我们可以用它们来控制光在空间中的传播方式。 这对于构建捕获图像的设备是至关重要的,并且必须在图像形成的数学模型中在一定程度上考虑。
透镜成像
光学系统(或相机)是由用来“直射”光的一组透镜组成。通过直射光,我们指的是传播方向的受控变化,这可以通过衍射,折射和反射来执行。为简单起见, 我们忽略了透镜系统中的衍射和反射的影响,我们只考虑折射,即只考虑最简单的模型,即黑盒子中的薄透镜(thin lens)模型,如图3所示。
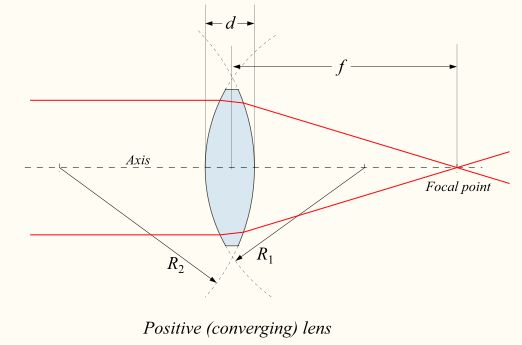
图3。薄透镜模型。如果透镜的厚度远小于其表面的曲率半径( d ≪ ∣ R 1 ∣ d\ll |R_1| d≪∣R1∣且 d ≪ ∣ R 2 ∣ d\ll |R_2| d≪∣R2∣),则可认为透镜是薄透镜。
薄透镜数学模型
薄透镜是由轴(称为光轴,optical axis)和垂直于轴的平面(称为焦平面,focal plane)定义的数学模型,具有以光学中心为中心的圆形孔,即焦平面与光轴的交点。薄透镜表示为一个参数,通常用 f f f 表示,称为焦距(focal length),和两个功能特性。

图4。平行于光轴的光线在焦点处相交。
首先,平行于光轴的所有光线进入光圈后与光轴交于与距离光学中心距离为 f f f的地方。交点被称为透镜的焦点(focus),见上图图4。
第二个特性是通过光学中心的所有光线都不会被偏转(即保持原方向)。
现在,考虑距离光轴不远处的点 p ∈ E 3 p\in \mathbb{E}^3 p∈E3,其沿着光轴方向与光学中心所在轴直线距离是 Z \rm Z Z(或许你可以把 p p p直线垂直投影到光轴,与光学中心距离是 Z \rm Z Z)。

图5。点 p p p的图像是平行于光轴的光线与通过光学中心的光线的交点的点 x \rm x x
现在从点 p p p 绘制两条光线:一条平行于光轴,一条通过光学中心,如上图图5所示。第一个与光轴在焦点处相交,第二个保持不受影响(通过薄透镜的定义特性)。
把 x \rm x x 称为这两条光线相交的点,并将 z z z 表示它与光学中心的距离(即点 x \rm x x投射到光轴上后与光学中心的距离)。
通过将来自 p p p 的任何其他光线分解成平行于光轴的分量和通过光学中心的分量,我们可以认为来自 p p p 的所有光线在透镜的相对侧上的 x x x 处相交。特别地,来自 x x x 平行于光轴的光线必须经过 p p p。使用相似三角形,我们获得了以下薄透镜的基本方程:
1 Z + 1 z = 1 f \frac{1}{Z}+\frac{1}{z}=\frac{1}{f} Z1+z1=f1
公式推导
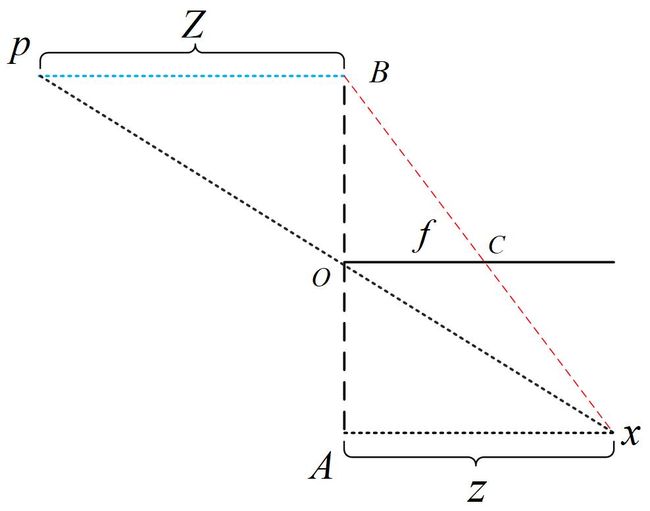
图6。相似三角形
利用相似三角形定理。我们可以得到
由于三角形 △ x O C ∼ △ x P B \triangle xOC \sim \triangle xPB △xOC∼△xPB,所以得到:
f Z = A O A B \frac{f}{Z}=\frac{AO}{AB} Zf=ABAO
同理由于三角形 △ B O C ∼ △ B A x \triangle BOC \sim \triangle BAx △BOC∼△BAx,得到
f z = O B A B \frac{f}{z}=\frac{OB}{AB} zf=ABOB
所以两个方程进行相加得到:
f Z + f z = A O + O B A B = 1 ⇔ 1 Z + 1 z = 1 f \frac{f}{Z}+\frac{f}{z}=\frac{AO+OB}{AB}=1 \Leftrightarrow \frac{1}{Z}+\frac{1}{z}=\frac{1}{f} Zf+zf=ABAO+OB=1⇔Z1+z1=f1
点 x x x 称为点 p p p 的像(image)。 因此,在薄透镜的假设下,在图像平面上坐标 ( x , y ) (x,y) (x,y)的点 x x x 处的辐照度 I ( x ) I(x) I(x)是通过对从由透镜的几何形状确定的锥体中包含的空间区域发射的所有能量进行积分而获得的。 如果这样的区域不包含光源,而只包含不透明的曲面,则有必要评估这些曲面如何向传感器辐射能量。在这里引出“视角”(field of view)的概念,它是从焦点看到的透镜光圈所对的角度。如果 D D D是镜头的直径,那么视野是是 2 arctan ( D / 2 f ) 2 \arctan(D/2f) 2arctan(D/2f)。
就还是图6来说, ∠ O C A \angle OCA ∠OCA是 ∠ A C B \angle ACB ∠ACB的一半,我们要求的是 ∠ A C B \angle ACB ∠ACB,假设大小为 α \alpha α。
然后在 △ A C O \triangle ACO △ACO中,由 tan \tan tan函数定义得到
tan ( α / 2 ) = O A O C = D / 2 f = D / 2 f \tan(\alpha/2)=\frac{OA}{OC}=\frac{D/2}{f}=D/2f tan(α/2)=OCOA=fD/2=D/2f
可以得到
α = 2 arctan ( D / 2 f ) \alpha = 2 \arctan (D/2f) α=2arctan(D/2f)
针孔成像
如果我们让薄透镜的孔径减小到零,则所有光线都被迫通过光学中心,因此它们不会发生光学偏转(方向不变)。 因此,锥体的孔径减小到零,并且唯一的点有助于在通过 p p p 的线上的点 x x x 处的辐照度。 如果我们让 p p p相对于以光学中心为中心的参考坐标系有坐标 X = [ X , Y , Z ] T {\rm X}=[X,Y,Z]^T X=[X,Y,Z]T,光轴为 Z Z Z轴,从图7中可以看出, x x x和 p p p的坐标通过理想的透视投影相关。
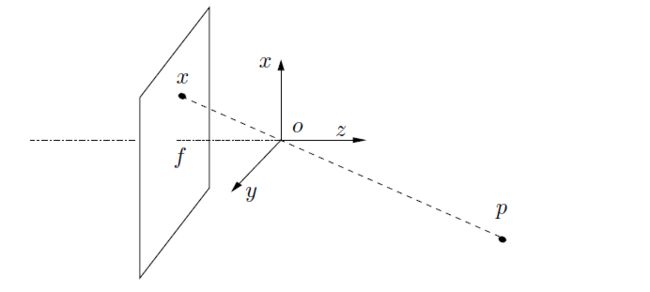
图7。点 p p p 的像是穿过光学中心 o o o 的光线与距光学中心距离 f f f 的图像平面的交点的点 x x x。
从图7,我们很难将空间点与图像点进行联系。这里采用高翔十四讲进行说明。
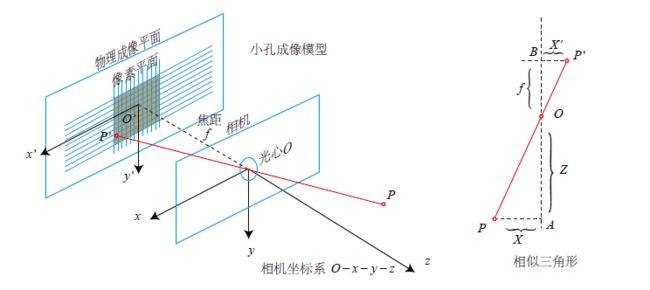
图8。针孔相机模型
然后对针孔模型建模,假设 O − x − y − z O-x-y-z O−x−y−z是相机坐标系,习惯上让 z z z轴指向相机前方, x x x向右, y y y向下。 O O O是相机光心也是针孔模型的针孔。从现实空间 P P P经过 O O O投影后落到成像平面 O ′ − x ′ − y ′ O^\prime-x^\prime-y^\prime O′−x′−y′上变成成像点 P ′ P^\prime P′。
先前的假设中 P P P点具有坐标 X = [ X , Y , Z ] T {\rm X}=[X,Y,Z]^T X=[X,Y,Z]T。假设点 P ′ P^\prime P′的坐标为 X ′ = [ X ′ , Y ′ , Z ′ ] T {\rm X}^\prime=[X^\prime,Y^\prime,Z^\prime]^T X′=[X′,Y′,Z′]T,由于已知物理成像平面到小孔距为 f f f,由图7可以得到由于相似三角形有:
(1) Z f = − X X ′ = − Y Y ′ \frac{Z}{f}=-\frac{X}{X^\prime}=-\frac{Y}{Y^\prime}\tag{1} fZ=−X′X=−Y′Y(1)
其中负号表示成的像是倒立的。
那么换到我们前面的图7的场景来看,假设 x x x具有图像平面坐标为 ( x , y ) (x,y) (x,y),那么应用(1)式后,我们可以得到
(2) x = − f X Z , y = − f Y Z x=-f\frac{X}{Z},y=-f\frac{Y}{Z}\tag{2} x=−fZX,y=−fZY(2)
有时候有些论文甚至书籍会将这个投影简化写成映射 π \pi π,即表示从3D点投影到2D平面上的射影映射。
π : R 3 → R 2 ; X ↦ x \pi :\mathbb{R}^3 \rightarrow \mathbb{R}^2;X \mapsto x π:R3→R2;X↦x
我们可以把关系写成 x = π ( X ) x=\pi(X) x=π(X)。
注意,通过 p p p的线上的任何其他点都可以投影到相同的坐标 [ x , y ] T [x,y]^T [x,y]T。 该成像模型是所谓的理想针孔相机模型。 之所以称为理想的,因为当光圈减小时,衍射影响占主导地位,因此(纯折射)薄透镜模型不成立,这点在1999年《Principles Of Optics》第七版的书中指出。
此外,随着孔径减小到零,通过透镜的能量也变为零。 尽管可以实际构建近似针孔相机的设备,但针孔模型只是良好聚焦的成像系统的几何近似,是纯几何模型。
请注意,无论是公式(1)还是(2)都有一个负号。 这使得物体的图像在图像平面(或人眼的视网膜)上看起来是颠倒的。 为了消除这种影响,我们可以简单地翻转这个图像: ( x , y ) ↦ ( − x , − y ) (x,y) \mapsto (-x,-y) (x,y)↦(−x,−y),如图8所示。 这相当于将图像平面 { Z = − f } \{Z=-f\} {Z=−f}置于光学中心的前面: { Z = + f } \{Z=+f\} {Z=+f},也就是把成像平面对称到相机前方,使得与三维空间点一同放在了相机坐标系的同一侧。
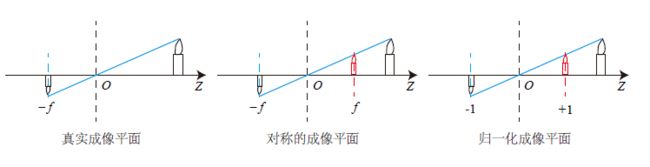
图9。真实成像平面,对称成像平面,归一化成像平面的图示。
这样之后,我们看一个物体的成像就类似于图10所示。
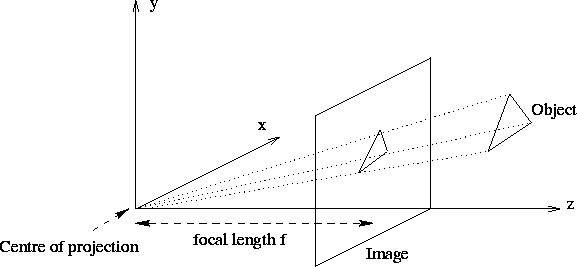
图10。成像平面位于空间点的同一侧。
我们把成像平面挪到前方是由于我们处理真实世界与相机投影的数学手段,而且大多数相机输出的图像并不是倒像——相机自身的软件会帮你翻转这张图像,所以你看到的一般是正着的像,也就是对称的成像平面上的像。
所以,尽管从物理原理来说,小孔成像应该是倒像,但由于对图像作了预处理,所以理解成在对称平面上的像,并不会带来什么坏处。
翻转之后我们就可以说,点 P P P被投影到图像平面上的点 x = [ x , y ] T {\rm x}=[x,y]^T x=[x,y]T具有如下关系:
(3) x = f X Z , y = f Y Z x=f\frac{X}{Z},y=f\frac{Y}{Z}\tag{3} x=fZX,y=fZY(3)
我们经常使用相同的符号 x \rm x x来表示齐次表示 [ f X / Z , f Y / Z , 1 ] T ∈ R 3 [fX/Z,fY/Z,1]^T\in \mathbb{R}^3 [fX/Z,fY/Z,1]T∈R3,只要维度从上下文中清楚即可。
博文内容总结
图像是二维亮度阵列,可以看成是如下的一个映射。
I : Ω ⊂ R 2 → R + ; ( x , y ) ↦ I ( x , y ) I:\Omega\sub \mathbb{R}^2 \rightarrow \mathbb{R}_+;(x,y)\mapsto I(x,y) I:Ω⊂R2→R+;(x,y)↦I(x,y)
I I I中的值(即亮度值),取决于所观察场景的物理属性,例如其形状,材料反射特性和光源分布。
薄透镜模型中存在一个如下的等式。
1 Z + 1 z = 1 f \frac{1}{Z}+\frac{1}{z}=\frac{1}{f} Z1+z1=f1
其中 f f f是焦距。 Z Z Z和 z z z分别是物体和成像距离光学中心所在轴的垂直线距离。
如果我们把薄透镜的孔径减小到零,就成为理想的针孔模型。
在理想的针孔模型下,3D点和2D点的投影映射如下:
π : R 3 → R 2 ; X ↦ x \pi :\mathbb{R}^3 \rightarrow \mathbb{R}^2;X \mapsto x π:R3→R2;X↦x
在现实的翻转成像后,如果3D点 P P P具有坐标 [ X , Y , Z ] T [X,Y,Z]^T [X,Y,Z]T,则投影点 x = [ x , y ] T {\rm x}=[x,y]^T x=[x,y]T具有如下关系:
x = f X Z , y = f Y Z x=f\frac{X}{Z},y=f\frac{Y}{Z} x=fZX,y=fZY
该点的齐次坐标表示为 [ f X / Z , f Y / Z , 1 ] T ∈ R 3 [fX/Z,fY/Z,1]^T\in \mathbb{R}^3 [fX/Z,fY/Z,1]T∈R3。