Week7_Support Vector Machines课后习题解答
大家好,今天和大家讨论一下coursera网站上Stanford University的机器学习第7周:Support Vector Machines的课后作业解答。我将给出这些题目和选项的翻译以及个人对题目的见解和看法,这些观点中有些可能是错误的,如有发现,请留言批评指正,谢谢。特此提醒,由于不同学生的题目参数,选项都会不同,请同学们不要照抄,因为我的答案给你可能完全是错误的答案,但是每道题的原理都是一样的。
这周的课程中,吴恩达老师主要向我们介绍了四大方面的内容。
1.SVM从逻辑回归算法的演化过程以及它的具体模型。
2.为何SVM算法又称Large Margin Classification,解释SVM的边界Margin的具体含义。
3.Kernal的具体定义以与SVM算法结合的使用方法。
4.SVM的具体使用步骤,linear kernel,Guassian kernel自定义kernel的选取原则。Multi-calss classification的分类方法。在不同训练样本数m和特征值个数n的情况下,如何选择Logistic regression,SVM or Neural Networks.
好的,话不多说,下面直接进入我们的习题解答。
1.第一题
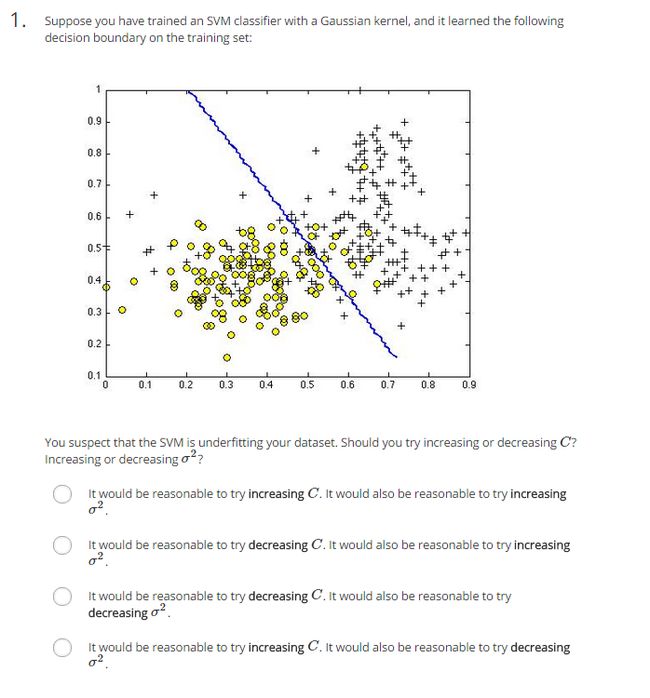
(1)题意:假设利用高斯核函数训练支持向量机,得到如下的决策线。你认为你的算法对数据集欠拟合的,你应该增大还是减小C?增大还是减少方差sigma^2?
a.增大C,增大sigma^2
b.减小C,增大sigma^2
c.减小C,减小sigma^2
d.增大C,减小sigma^2
(2)分析:C=1/lambda,由于是欠拟合,我们需要减小lambda,即增大C。增大sigma^2会使曲线变得更加平缓,使模型more like underfit,故我们要减小sigma^2。
(3)答案:d
2.第二题
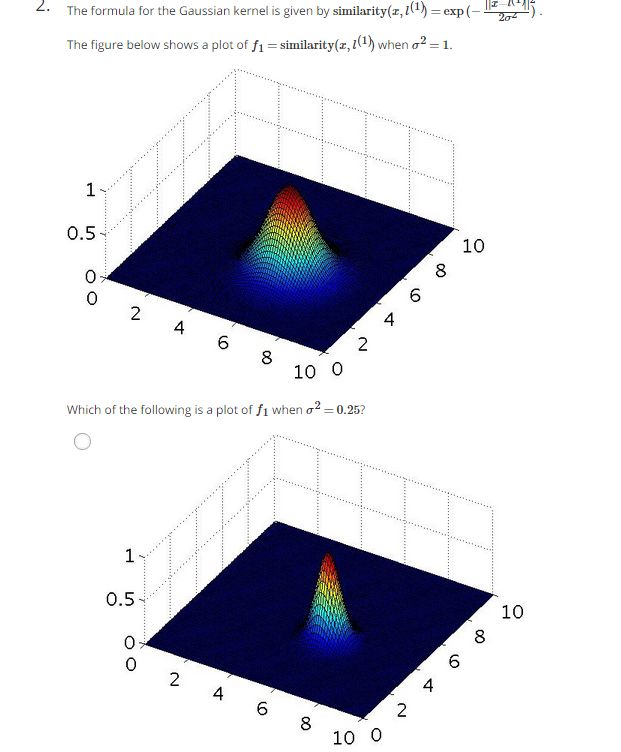
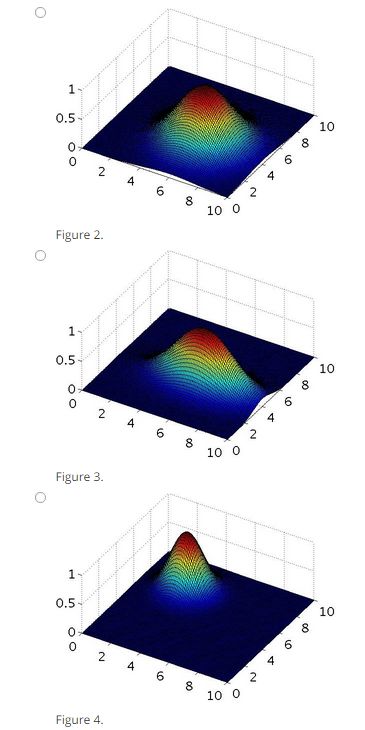
(1)题意:给定高斯核函数如题目中式子所示,下面这张图画的是f1在sigma^2=1情况下的分布图形,请问下面四张途中哪张是sigma^2=0.25时的分布图形?
(2)分析:首先,我们看到图形的中心在(5,5)左右,改变sigma的值是不会改变中心的。其次,减小sigma的值,曲线会变得更加尖锐,曲线的斜率会加大,更加陡峭。
a.曲线中心还是(5,5)而且变陡峭了,正确。
b.曲线中心还素(5,5)但是曲线便舒缓的,错误。
c.曲线在两个维度上的舒缓成都不同,但是题目图中是相同的,错误。
d.曲线的中心不再(5,5),而且舒缓程度不变,错误。
(3)答案:a
3.第三题
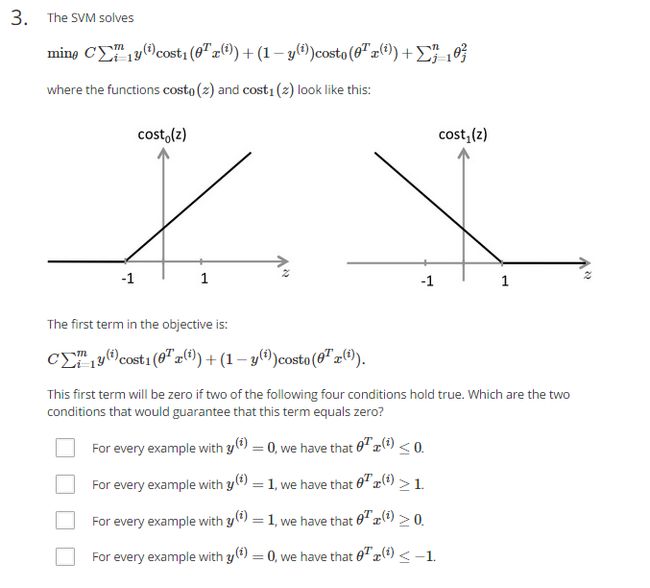
(1)题意:SVM要解决的就是最小化题目中所示的式子,其中cost0(z)和cost1(z)的图形如题中所示。当下面哪两个条件为0时,式子的第一部分的值为0?
a.对于任何y=0,theta’*x小于等于0
b.对于任何y=1,theta’*x大于等于1
c.对于任何y=1,theta’*x大于等于0
d.对于任何y=0,tehta’*x小于等于-1
(2)分析:从上面的图中就可以看出,放y=0时,cost0(z)的值在z小于等于-1时为0;当y=1时,cost1(z)在z大于等于1时为0,故选择b,d。注意,SVM的代价函数是从逻辑回归的代价函数发展而来的,对于逻辑回归的分类,我们选择a,c,但是他的前面那项也不能为0.
(3)答案:b,d
4.第四题

(1)题意:假设我么的数据的特征值数n=10,共有m=5000个训练样本。在利用梯度下降的方法计算逻辑回归分类器后,你发现分类器欠拟合,对训练样本和交叉验证样本没能达成预期的效果。请选择下面所有可以解决这个问题的选项。
a.使用含有很多隐藏单元的神经网络
b.使用不同的最优化算法,因为使用梯度下降的算法训练逻辑回归也许达到的是局部最小值。
c.减小训练集的样本数
d.添加更多新的多项式特征,如:x1x2,x1x2x3等
(2)分析:吴恩达老师在视频中说过,对于n很大(10000),m较小(10-1000),使用逻辑回归算法或者无核函数的SVM算法;当n较小(1-1000),m中等大小(10-10000)时,用SVM算法;当n较小(1-1000),m很大(大于50000)时,创造更多的特征值,再用逻辑回归或者无核函数的SVM算法。神经网络适用于以上任何情况,单数训练速度慢。
a.由于神经网络的隐藏单元越多,对训练样本的你和程度越高。神经网络也可用于体重所给的n,m,故正确。
b.个人觉得错误,可能利用梯度下降算法得到的当前的最小值是局部最小值,这个位置的你和程度不是很高,如果利用不同的最优化算法可能也会达到这个点。其实只要改变初始化theta即可,不用改变最优化算法。
c.减小训练样本数并不能解决欠拟合问题,在第六章中的learning curves中已经给出解释,不选。
d.由于是欠拟合,所以增加一些多项式特征可以帮助欠拟合,正确。
(3)答案:a,d
5.第五题

(1)题意:选出下面所有正确的陈述。
a.高斯核函数的最大值为1
b.如果数据是线性可分的(决策先为直线),一个无核函数的SVM算法都会返回相同的参数theta,无论如何改变C的值。
c.如果你利用一对多的方法训练SVM算法,不能用任何核函数。
d.假设你有2维的输入样本,线性核函数(无核函数)的SVM算法得到是决策线是一条直线
(2)分析:
a.正确,最大为1最小为0,值越大表示越相似。
b.正确,因为数据都是线性可分的了,所以前面哪项的值完全可以等于0,改变C的值无意义,不会影响参数theta的取值。
c.错误,one-vs-all是先把一类自成一类,其余类看成第二类,这样就化解为2类的SVM计算问题。而解决这种问题完全可以用核函数。
d.正确,因为是无核函数,则theta’f = theta’ x = theta0*x0+theta1*x1+theta2*x2,为直线.
(3)答案:a,b,d
这道题博主也做错了,个人感觉是b或者d中其中一个选项错了,但不知道到底是哪个,求学霸解答!