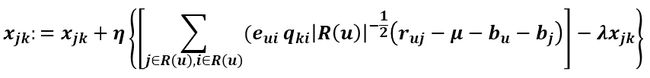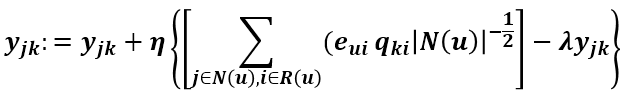奇异值分解（SVD）及其扩展详解

　　 SVD是一种常用的矩阵分解技术，是一种有效的代数特征提取方法。SVD在协同过滤中的主要思路是根据已有的评分情况，分析出评分者对各个因子的喜好程度以及电影包含各个因子的程度，最后再反过来分析数据得出预测结果。RSVD、SVD++、ASVD是基于SVD的改进算法。

本文算法主要考虑个性化推荐领域

1.Matrix Factorization Model 和 Baseline Predictors

　　 SVD其实就是Matrix Factorization Model和Baseline Predictor的结合，所以为了方便我们先在这里介绍这两个东西。

（1）Matrix Factorization Model

　　 把我们的用户评分想象成一个表：

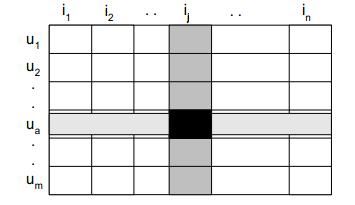
　　 每一行代表一个用户,每一列代表一个物品,这其实就是一个矩形,只是我们拥有的这个矩形可能是非常稀疏的,也就是我们知道的评分占总量很少,,但现在我们知道它是一个矩形,一个矩形自然可以表示为另两个矩形的乘积（后续会给出证明）:

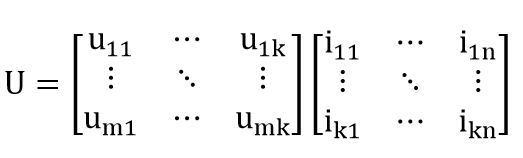
　　 将这种分解方式体现协同过滤中，即有：

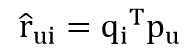
　　 在这样的分解模型中,Pu代表用户隐因子矩阵（表示用户u对因子k的喜好程度),Qi表示电影隐因子矩阵（表示电影i在因子k上的程度）。

（2）Baseline Predictors

　　 Baseline Predictors使用向量bi表示电影i的评分相对于平均评分的偏差，向量bu表示用户u做出的评分相对于平均评分的偏差，将平均评分记做μ。

2.SVD数学原理及推导

　　 对任意M*N的矩阵，能否找到一组正交基使得经过它变换后还是正交基？答案是肯定的，它就是SVD分解的精髓所在。

　　 现在假设存在M*N矩阵A，事实上，A矩阵将n维空间中的向量映射到k（k<=m）维空间中，k=Rank(A)。现在的目标就是：在n维空间中找一组正交基，使得经过A变换后还是正交的。假设已经找到这样一组正交基：

则A矩阵将这组基映射为：

如果要使他们两两正交，即

根据假设，存在

所以如果正交基v选择为A’A的特征向量的话，由于A’A是对称阵，v之间两两正交，那么

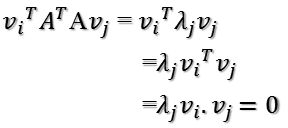
这样就找到了正交基使其映射后还是正交基了，现在，将映射后的正交基单位化：

因为

所以有

所以取单位向量

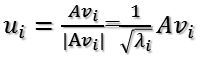
由此可得

---

　　 当k < i <= m时，对u1，u2，…，uk进行扩展u(k+1),…,um，使得u1，u2，…，um为m维空间中的一组正交基，即将{u1，u2，…，uk}正交基扩展成{u1，u2，…，um}单位正交基。同样的，对v1，v2，…，vk进行扩展v(k+1),…,vn（这n-k个向量存在于A的零空间中，即Ax=0的解空间的基），使得v1，v2，…，vn为n维空间中的一组正交基。

---

则可得到

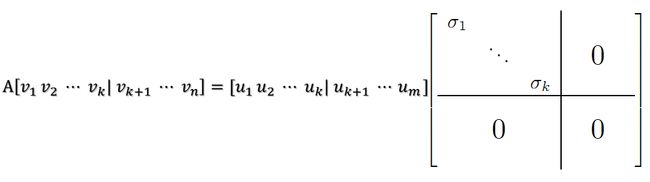
继而可以得到A矩阵的奇异值分解（两边同乘以VT）：

V是n×n的正交阵，U是n×n的正交阵，∑是n×m的对角阵

　　 现在可以来对A矩阵的映射过程进行分析了：如果在n维空间中找到一个（超）矩形，其边都落在A’A的特征向量的方向上，那么经过A变换后的形状仍然为（超）矩形！

　　 vi为A’A的特征向量，称为A的右奇异向量，ui=Avi实际上为AA’的特征向量，称为A的左奇异向量。下面利用SVD证明文章一开始的满秩分解：

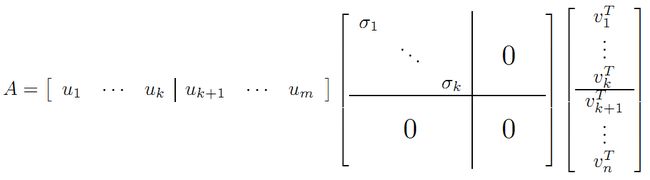
利用矩阵分块乘法展开得：

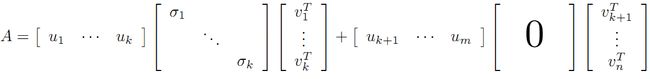
可以看到第二项为0，有

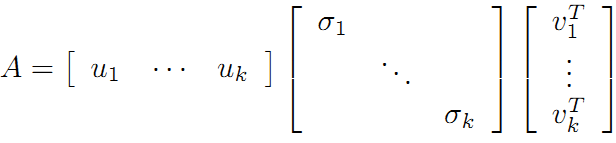
令

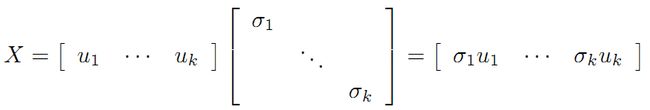
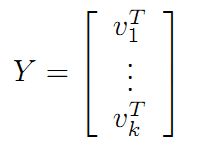
则A=XY即是A的满秩分解。

3.Basic SVD

　　 如上所证，评分矩阵R存在这样一个分解，所以可以用两个矩阵P和Q的乘积来表示评分矩阵R：

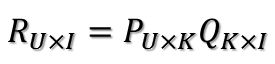
　　 U表示用户数，I表示商品数，K=Rank(R)。然后就是利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分，那么未知的评分也就可以用P的某一行乘上Q的某一列得到了：

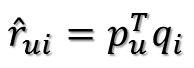
　　 这是预测用户u对商品i的评分，它等于P矩阵的第u行乘上Q矩阵的第i列。这个是最基本的SVD算法，那么如何通过已知评分训练得到P和Q的具体数值呢？

假设已知的评分为：

则真实值与预测值的误差为：

继而可以计算出总的误差平方和：

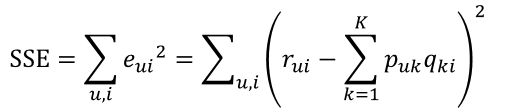
只要通过训练把SSE降到最小那么P、Q就能最好地拟合R了。那又如何使SSE降到最小呢（本文使用梯度下降优化方法）？

---

利用梯度下降法可以求得SSE在Puk变量（也就是P矩阵的第u行第k列的值）处的梯度：

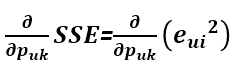
利用求导链式法则，e^2先对e求导再乘以e对Puk的求导：

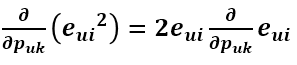
由于

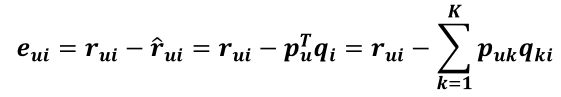
所以

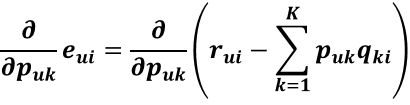
上式中括号里的那一坨式子如果展开来看的话，其与Puk有关的项只有PukQki，其他的无关项对Puk的求导均等于0,所以求导结果为：

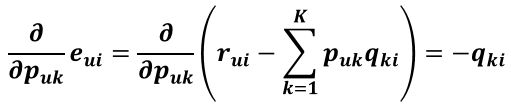
所以

为了让式子更简洁，令

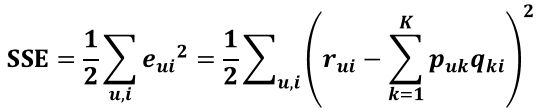
这样做对结果没有影响，只是为了把求导结果前的2去掉，更好看点。得到

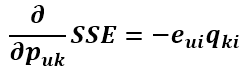
现在得到了目标函数在Puk处的梯度了，那么按照梯度下降法，将Puk往负梯度方向变化。令更新的步长（也就是学习速率）为

则Puk的更新式为

同样的方式可得到Qik的更新式为

得到了更新的式子，现在开始来讨论这个更新要怎么进行。有两种选择：1、计算完所有已知评分的预测误差后再对P、Q进行更新。2、每计算完一个eui后立即对Pu和qi进行更新。这两种方式都有名称，分别叫：1、批梯度下降。2、随机梯度下降。两者的区别就是批梯度下降在下一轮迭代才能使用本次迭代的更新值，随机梯度下降本次迭代中当前样本使用的值可能就是上一个样本更新的值。由于随机性可以带来很多好处，比如有利于避免局部最优解，所以现在大多倾向于使用随机梯度下降进行更新。

4.RSVD

　　 上面就是基本的SVD算法，但是，问题来了，上面的训练是针对已知评分数据的，过分地拟合这部分数据有可能导致模型的测试效果很差，在测试集上面表现很糟糕，这就是过拟合问题。

　　 那么如何避免过拟合呢？那就是在目标函数中加入正则化参数（加入惩罚项），对于目标函数来说，P矩阵和Q矩阵中的所有值都是变量，这些变量在不知道哪个变量会带来过拟合的情况下，对所有变量都进行惩罚：

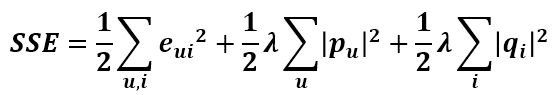
这时候目标函数对Puk的导数就发生变化了，现在就来求加入惩罚项后的导数。

括号里第一项对Puk的求导前面已经求过了，第二项对Puk的求导很容易求得，第三项与Puk无关，导数为0，所以

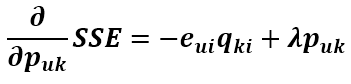
同理可得SSE对qik的导数为

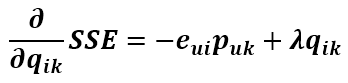
将这两个变量往负梯度方向变化，则更新式为

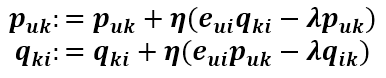
这就是正则化后的SVD，也叫RSVD。

5.加入偏置的SVD、RSVD

　　 关于SVD算法的变种太多了，叫法也不统一，在预测式子上加点参数又会出来一个名称。由于用户对商品的打分不仅取决于用户和商品间的某种关系，还取决于用户和商品独有的性质，Koren将SVD的预测公式改成这样

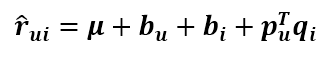
第一项为总的平均分，bu为用户u的属性值，bi为商品i的属性值，加入的这两个变量在SSE式子中同样需要惩罚，那么SSE就变成了下面这样：

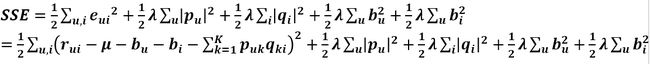
由上式可以看出SSE对Puk和qik的导数都没有变化，但此时多了bu和bi变量，同样要求出其更新式。首先求SSE对bu的导数，只有第一项和第四项和bu有关，第一项对bu的求导和之前的求导类似，用链式法则即可求得，第四项直接求导即可，最后可得偏导数为

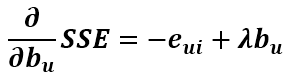
同理可得对bi的导数为

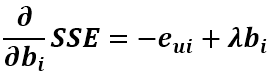
所以往其负梯度方向变化得到其更新式为

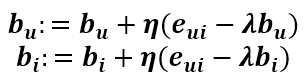
这就是加入偏置后的SVD（RSVD）。

6.Asymmetric-SVD(ASVD)

　　 全称叫Asymmetric-SVD，即非对称SVD，其预测式子为

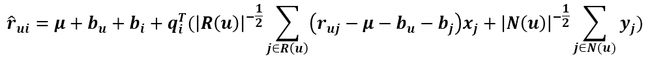
R(u)表示用户u评过分的商品集合，N(u)表示用户u浏览过但没有评过分的商品集合，Xj和Yj是商品的属性。

这个模型很有意思，看预测式子，用户矩阵P已经被去掉了，取而代之的是利用用户评过分的商品和用户浏览过尚未评分的商品属性来表示用户属性，这有一定的合理性，因为用户的行为记录本身就能反应用户的喜好。而且，这个模型可以带来一个很大的好处，一个商场或者网站的用户数成千上万甚至过亿，存储用户属性的二维矩阵会占用巨大的存储空间，而商品数却没有那么多，所以这个模型的好处显而易见。但是它有个缺点，就是迭代时间太长了，这是可以预见的，以时间换空间嘛。

同样的，需要计算其各个参数的偏导数，求出更新式，显然，bu和bi的更新式和刚才求出的一样

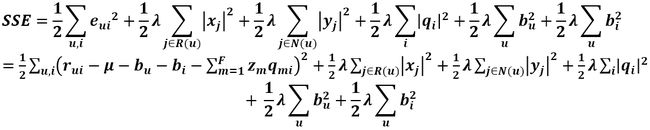
其中的向量z如下：

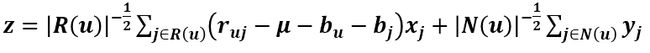
现在要求qik、x和y的更新式，在这里如果把z看成Pu则根据前面求得的更新式可得qik的更新式：

求Xj的导数需要有点耐心，SSE的第二项对Xj的导数很容易得到，现在来求第一项对Xj的导数：

上式求和符号中的i,j都是属于R(u)的，可以看到Zm只有当m==k时才与Xjk有关，所以

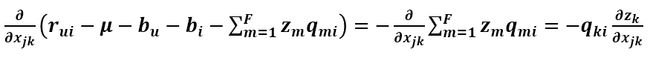
因为

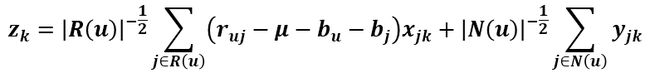
所以

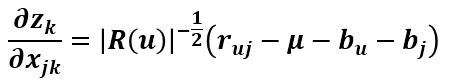
所以得到SSE对Xjk的导数为

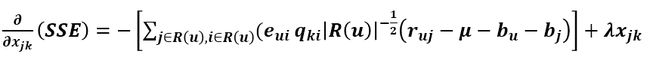
同理可得SSE对Yjk的导数为

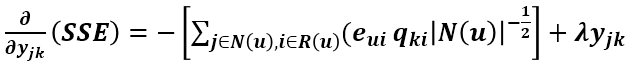
所以得到Xjk和Yjk的更新方程

这就叫非对称SVD（ASVD）

7.SVD++

这个模型也是Koren文章中提到的，SVDPlusPlus（SVD++），它的预测式子为

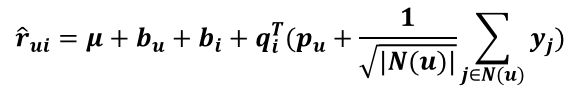
这里的N(u)表示用户u行为记录（包括浏览的和评过分的商品集合）。看了ASVD的更新式推导过程再来看这个应该很简单，Puk和qik的更新式子不变，Yjk的更新式子和ASVD的更新式一样：

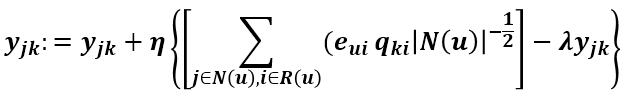
这些就是Koren在NetFlix大赛中用到的SVD算法

8.对偶算法

将前面预测公式中的u和i调换位置得到其对偶算法，对于RSVD而言，u和i的位置是等价的、对称的，所以其对偶算法和其本身没有区别，但对于ASVD和SVD++则不同，有时候对偶算法得到的结果更加精确，并且，如果将对偶算法和原始算法的预测结果融合在一起的话，效果的提升会让你吃惊！

对偶的ASVD预测公式：

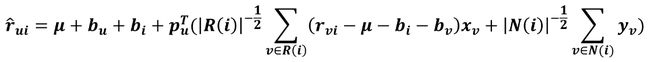
这里R(i)表示评论过商品i的用户集合，N(i)表示浏览过商品i但没有评论的用户集合。由于用户数量庞大，所以对偶的ASVD会占用很大空间，这里需要做取舍了。

对偶的SVD++预测公式：

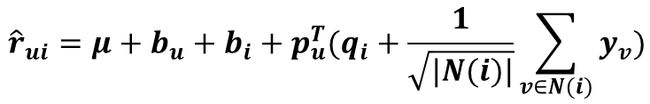
这里N(i)表示对商品i有过行为（浏览或评分）的用户集合。

实现这一对偶的操作其实很简单，只要读取数据的时候把用户id和商品id对调位置即可，也就是将R矩阵转置后再训练。

9.SVD实战

任务介绍：

数据集：MovieLens100k 的 u1数据
算法：有偏置的SVD（具体参数更新公式可以看第5部分）
评价指标：RMSE

# -*- coding: utf-8 -*-

from __future__ import print_function  #引入python 3.x print函数
from __future__ import division  #精准除法

import numpy as np

def load_data(path):
    data = []
    with open(name=path,mode='r') as file:
        for line in file:
            (user_id,moive_id,rating,time_stamp) = line.strip().split('\t')
            data.append([user_id,moive_id,rating])
    data = np.array(data).astype(np.uint16)
    return data

#重要变量  ave,bi,bu,qi,qu
#核心参数  k(rank),gamma（学习速率）,Lambda(正则项系数)

class  SVD:
    def __init__(self,X,k=20):
        '''''
            k  is the length of vector
        '''
        self.X=np.array(X)
        self.k=k
        self.ave=np.mean(self.X[:,2])
        print("the train data size is ",self.X.shape)
        self.bi={}
        self.bu={}
        self.qi={}
        self.pu={}
        self.movie_user={}
        self.user_movie={}
        for i in range(self.X.shape[0]):
            uid=self.X[i][0]
            mid=self.X[i][1]
            rat=self.X[i][2]
            self.movie_user.setdefault(mid,{})
            self.user_movie.setdefault(uid,{})
            self.movie_user[mid][uid]=rat
            self.user_movie[uid][mid]=rat
            self.bi.setdefault(mid,0)
            self.bu.setdefault(uid,0)
            self.qi.setdefault(mid,np.random.random((self.k,1))/10*(np.sqrt(self.k)))
            self.pu.setdefault(uid,np.random.random((self.k,1))/10*(np.sqrt(self.k)))

    def pred(self,uid,mid):
        self.bi.setdefault(mid,0)
        self.bu.setdefault(uid,0)
        self.qi.setdefault(mid,np.zeros((self.k,1)))
        self.pu.setdefault(uid,np.zeros((self.k,1)))
        if (self.qi[mid]==None):
            self.qi[mid]=np.zeros((self.k,1))
        if (self.pu[uid]==None):
            self.pu[uid]=np.zeros((self.k,1))
        ans=self.ave+self.bi[mid]+self.bu[uid]+np.sum(self.qi[mid]*self.pu[uid])
        if ans>5:
            return 5
        elif ans<1:
            return 1
        return ans

    def train(self,steps=20,gamma=0.04,Lambda=0.15):
        for step in range(steps):
            print('the ',step,'th  step is running')
            rmse_sum=0.0
            kk=np.random.permutation(self.X.shape[0])    #np.random.permutation(5)  [3,1,2,0,4] 顺序打乱
            for j in range(self.X.shape[0]):
                i=kk[j]
                uid=self.X[i][0]
                mid=self.X[i][1]
                rat=self.X[i][2]
                #参数更新
                eui=rat-self.pred(uid,mid)
                rmse_sum+=eui**2
                self.bu[uid]+=gamma*(eui-Lambda*self.bu[uid])
                self.bi[mid]+=gamma*(eui-Lambda*self.bi[mid])
                temp=self.qi[mid]
                self.qi[mid]+=gamma*(eui*self.pu[uid]-Lambda*self.qi[mid])
                self.pu[uid]+=gamma*(eui*temp-Lambda*self.pu[uid])
            #学习速率递减
            gamma=gamma*0.93
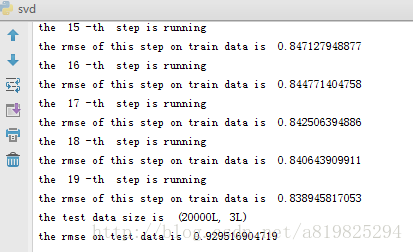
            print("the rmse of this step on train data is ",np.sqrt(rmse_sum/self.X.shape[0]))

    def test(self,test_X):
        output=[]
        sums=0
        test_X=np.array(test_X)
        print("the test data size is ",test_X.shape)
        for i in range(test_X.shape[0]):
            pre=self.pred(test_X[i][0],test_X[i][1])
            output.append(pre)
            sums+=(pre-test_X[i][2])**2
        rmse=np.sqrt(sums/test_X.shape[0])
        print("the rmse on test data is ",rmse)
        return output

train_data = load_data('./ml-100k/u1.base')
test_data = load_data('./ml-100k/u1.test')

svd = SVD(train_data,k=30)
svd.train(steps=20,gamma=0.04,Lambda=0.15)
svd.test(test_data)

运行结果：