【笔试代码题记录】20190803网易/猿辅导
文章目录
- 网易
- 1. 倒数排列
- 2. 数字能否成环
- 3. 序列交换
- 4. 优秀的01序列
- 猿辅导
- 1. 字符串解码
- 2. 走迷宫
- 3. 击鼓传花
网易
网易2020校招笔试编程参考思路和代码
1. 倒数排列
题目描述:给定整数n,对数字n按字典序进行全排列,给定其中一个排列,假设它是正数第Q个排列,求倒数第Q个排列是什么。
例如,1到3的所有全排列为:[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
当给定 排列[1,2,3](正数第一个排列)时,需要返回[3,2,1](倒数第一个排列);当给定排列[1,3,2]时,需要返回[3,1,2]。
解法一(全排列,超时,通过率40%):对n个数字进行全排列,可以得到全排列的列表res,然后找出给定的排列在res中的位置下标,得到Q值,从res末尾开始,输出第Q个排列即可。
class Solution:
def permute(self, n, list):
if not n:
return
nums = [(i + 1) for i in range(n)]
if len(nums) == 1:
return [nums]
res = []
self.helper(nums, res, [])
for i in range(len(res)):
if res[i] == list:
index = i
break
return " ".join(str(i) for i in res[len(res)-index - 1])
def helper(self, nums, res, path):
if not nums:
res.append(path)
return
for i, num in enumerate(nums):
self.helper(nums[:i] + nums[i +1:], res, path + [num])
n = int(input()) # 输入n
list = list(map(int, input().split())) # 输入n个数字的某一个排列
s = Solution()
print(s.permute(n, list))
解法二(找规律,重要):从上面的例子可以看出来,正数第Q个排列和倒数第Q个排列有如下关系:每一位数字和加起来都等于n + 1! 有了这个规律,可以拿给定的排列直接计算出倒数第Q个排列,根本不需要求n个数字的全排列。
def func(n, list):
for i in range(n):
list[i] = n + 1 - list[i]
return " ".join(str(i) for i in list)
n = int(input())
list = list(map(int, input().split()))
print(func(n, list))
2. 数字能否成环
题目描述:长度为n的数组,能否组成一个环(首尾链接),使得环中每个数字都小于它相邻的两个数字之和(每个数字必须使用而且只能使用一次)。(题目中给定n大于等于3)
解法:对数组nums进行降序排序,判断nums[0] < nums[1] + nums[-1]即可。因为题目问的是能不能成环,最简单的方法就是将排好序的数组顺序相连,最后将首尾相连即可。只要最大的元素满足限制条件,剩余的元素一定满足条件。 比较简单,代码就不写了,通过率100%。
3. 序列交换
题目描述:给定一个包含n个数字的数组,可以对这个数组执行任意次以下交换操作:
对于数组中的两个下标i和j,如果a[i] + a[j] 为奇数,就可以交换a[i]和a[j]。交换次数不限制。求解在通过若干次操作后得到的数组中,字典序最小的是什么。
【输入描述】:
第一行输入n,表示数组长度,
第二行为n个整数,代表数组的元素。
【输出描述】:
输出经过 若干次交换后,字典序最小的数组
示例
输入:
4
7 3 5 1
输出:
7 3 5 1
输入:
5
3 1 5 2 4
输出:
3 5 1 4 2
解题思路:只要数组中同时出现了奇数和偶数,那么直接对数组进行排序即可。(参考牛客网大神解答)
def func(nums):
if not nums or len(nums) == 1:
return nums
odd, even = 0, 0
for i in range(len(nums)):
if nums[i] % 2== 1:
odd += 1
else:
even += 1
if odd > 0 and even > 0:
nums = sorted(nums)
return " ".join(str(i) for i in nums)
# n = int(input())
# list = list(map(int, input().split()))
n = 4
list = [53941, 38641, 31525, 75864, 29026, 12199, 83522, 58200, 64784, 80987]
print(func(list))
4. 优秀的01序列
给定一个优秀的01序列S,再给定一个序列T,判断T是否为优秀的01序列。优秀的01序列定义为:
- 如果序列S、T是优秀的,那么序列S+T是优秀的,+被定义为按顺序连接两个序列。
- 如果序列S是优秀的,那么reverse(S)也是优秀的,reverse(S)是S序列的按位取反,并删去前导零。例如reverse(“1100101”) = “11010”
【输入描述】:
第一行输入t,表示t组数据
对于每组数据,接下来的两行,一行为优秀的01序列S,一行为需要判断的01序列T,S和T都不含前导零
【输出描述】:
对于每组数据,输出YES或NO,表示序列T是否为优秀序列。
示例1:
输入:
1
1100
110011
输出:
YES
示例2:
输入:
1
1000
100001111
输出:
NO
我的思路如图(通过率0%,哭唧唧):
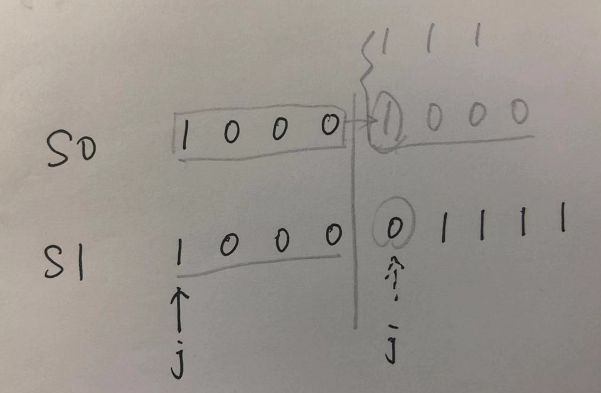
- 当s0的长度大于s1的长度时,只能通过反转s0来匹配。(这里有个小技巧,没必要一上手就反转,可以先判断s0[0]是否为0,如果是0的话,即使反转了,长度也不会减小,所以直接return False即可,否则就反转s0,尝试和s1匹配)
- 当s0长度小于s1的长度时,一段一段的来尝试匹配,设置一个指针j,先匹配s1的前len(s0)位,如果都匹配成功了,那么j指针后移len(s0)位,匹配下一段,如果匹配没成功,那么j指针回到这一段的起始点,并且反转s0为s0_change,尝试用s0_change字符串来匹配,如果匹配成功,则指针j往后移len(s0_change)这么多位,如果匹配失败,说明s0和s0_change都无法匹配,直接返回NO。
后来坚持发现笔试的时候代码逻辑有错,下面是修改后的版本,但是由于已经无法调试了,不知道对不对。
def func(s0, s1): # s0代表题目中的S,s1代表题目中的T
if not s0 or len(s0) == 1:
return "YES"
s0_change = change(s0) # 记录字符串reverse(s0)
def less(s0, s1): # 如果s0长度大于s1,只能反转
if s0[0] == 0: # s0的第一位如果是0,就算反转了,长度也不会减少,所以没必要比较
return "NO"
if s0_change != s1:
return "NO"
else:
return "YES"
if len(s0) > len(s1):
return less(s0, s1)
j = 0 # 一段一段匹配
while j < len(s1):
if len(s1) - j < len(s0): # s1最后剩下的如果小于s0的长度,尝试反转匹配
return less(s0, s1[j:])
j_copy = j
for i in range(len(s0)):
if s0[i] == s1[j_copy + i]:
j += 1
else:
break
if j == len(s0) + j_copy: # 匹配上了len(s0)这么长,需要将j指针后移,匹配下一段
continue
else:
j = j_copy # 没匹配上,j回到待匹配的初始点j_copy
for i in range(len(s0_change)):
if s0_change[i] == s1[j_copy + i]:
j += 1
else:
break
if j == len(s0_change) + j_copy: # 看反转后的字符串s0是否匹配成功
j += 1
continue
else:
return "NO" # 如果s0和s0_change都匹配失败,则返回“NO”
def change(s0): # 实现对序列S的reverse功能
nums = list(int(i) for i in s0)
for i in range(len(nums)):
nums[i] = 1 - nums[i]
res = "".join(str(i) for i in nums)
return res.lstrip('0') # 删去前导零
s0, s1 = "1000", "100001111" # 输出为NO
# s0, s1 = "1100", "110011" # 输出为YES
print(func(s0, s1))
分享一下大神的分析,动态规划,使用变量f[i][0/1]表示前i位是否优秀,且拼接的最后一个01串是不是初始序列SSS。按定义转移即可。
https://www.nowcoder.com/discuss/216237
猿辅导
1. 字符串解码
已知字符串有压缩规则为:
- AAAB可以压缩为A3B(单字符压缩不加括号)
- ABABA可以压缩为( AB)2A。
其中,输入数据保证不会出现冗余符号,且表示重复的数字一定合法且大于1,即不会出现:
3. (A)2B——应为A2B
4. ((AB))2C——应为(AB)2C
5. (A)B——应为AB
6. A1B, (AB)1C ——应为AB, ABC
注意,数字可能出现多位数即A11B或者(AB)10C或者A02这种情况。
A11B = AAAAAAAAAAAB
(AB)10C = ABABABABABABABABABABC
A02 = AA
示例输入:
A11B
(AA)2A
((A2B)2)2G
(YUANFUDAO)2JIAYOU
A2BC4D2
输出:
AAAAAAAAAAAB
AAAAA
AABAABAABAABG
YUANFUDAOYUANFUDAOJIAYOU
AABCCCCDD
我的思路,借鉴上次的字符串解码问题,进行了简单的改进,对于测试用例((A2B)2)2G无法通过,其余是可以通过的。无法通过的原因是两个2,只算了第一个,
def func(s):
if not s or len(s) == 1:
return s
stack = []
res = []
num = ""
i = 0
ss = ""
while i < len(s):
ch = s[i]
if ch.isdigit():
num += ch
while i + 1 < len(s) and s[i + 1].isdigit():
num += s[i + 1]
i += 1
if stack:
data = stack.pop()
string, _ = data[0], data[1]
if stack:
stack[-1][0] += string * int(num)
num = ""
else:
res += string * int(num)
num = ""
else:
if len(ss) > 1:
res += ss[:-1] + ss[-1] * int(num)
else:
res += ss * int(num)
ss = ""
num = ""
elif ch == '(':
stack.append(["", ""])
elif ch == ')':
i += 1
continue
else:
if stack:
stack[-1][0] += ch
else:
ss += ch
i += 1
if ss:
res += ss
return "".join(res)
s = "A2BC4D2"
print(func(s))
2. 走迷宫
一个N*M的迷宫,迷宫的每一个格子有一个数值,只能朝上下左右四个方向走,并且只能进入数值更大的格子。但是有紧急按钮,可以破例走向数值小的格子,按钮只能按k次。问,从迷宫中任选一个点出发,在紧急按钮的帮助下,最多可以走多少步。(开始位置也算步数,即站在起点步数为1)
解题思路:动态规划, 从每个位置出发,统计用k次机会的最长距离。【参考此贴评论13#】
line1 = '3 3 1' # 表示3行 3列 按钮可以按1次
line2 = "1 3 3\n2 4 9\n8 9 2" # 矩阵的数值
X, Y, K = map(int, line1.split(' '))
maps = [[int(y) for y in x.split(' ')] for x in line2.split('\n')]
def get_next_step(maps, pos, X, Y, K):
x, y = pos
num = maps[x][y]
up = maps[x - 1][y] if x > 0 else None
right = maps[x][y + 1] if y < Y - 1 else None
down = maps[x + 1][y] if x < X - 1 else None
left = maps[x][y - 1] if y > 0 else None
flag, i = [0, 0, 0, 0], 0
for dpos, item in zip([(-1, 0), (0, 1), (1, 0), (0, -1)], [up, right, down, left]):
if item:
if item > num:
new_pos = pos[0] + dpos[0], pos[1] + dpos[1]
flag[i] += 1
flag[i] += get_next_step(maps, new_pos, X, Y, K)
elif K > 0:
new_pos = pos[0] + dpos[0], pos[1] + dpos[1]
flag[i] += 1
flag[i] += get_next_step(maps, new_pos, X, Y, K - 1)
else:
flag[i] = 0
i += 1
return max(flag)
max_steps = 0
for x in range(X):
for y in range(Y):
steps = get_next_step(maps, (x, y), X, Y, K)
if steps >= max_steps:
max_steps = steps
print(max_steps + 1)
3. 击鼓传花
K个人玩击鼓传花,每击一次鼓,需要将花传一次,不能留在自己手中,游戏开始前,花在小原手中,求击了N次鼓后,这朵花又回到小原手中的方案数。输出这个数模1000000007后的结果。
输入两个数N和K,输出方案数。
例如,输入3和3,输出2.