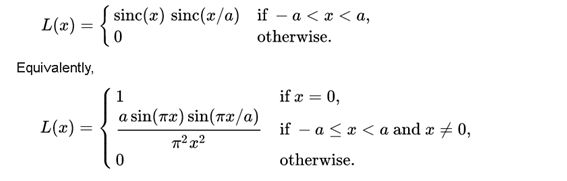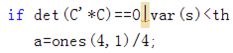图像缩放算法小结
参考网址:
https://blog.csdn.net/lfz_sau/article/details/51366700
http://www.cnblogs.com/blfshiye/p/4823027.html
https://en.wikipedia.org/wiki/Lanczos_resampling
https://wenku.baidu.com/view/22b38b70a417866fb84a8ea1.html
https://en.wikipedia.org/wiki/Pixel-art_scaling_algorithms
https://blog.csdn.net/u011630458/article/details/69524582
图像缩放的基本原理就是根据原图像的像素值通过一定的规则计算得到目标图像的像素值。
图像缩放的两个关键问题是应该选取原图像中哪些像素值,以及如何确定选取的像素值的权重。
图像缩放的常见问题是产生锯齿(缩小)或者模糊(放大)。
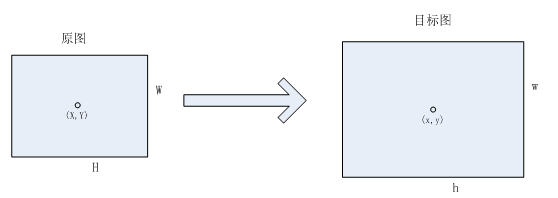
缩放图像是二维的尺度伸缩变换,目标图像的像素值从原图像得到。
令h_step = H/h, w_step = W/w,目标图中相邻像素的距离就转换为了原图中的h_step和w_step(通常不是整数)。
此外,原图和目标图的第一个像素重合。
最近邻算法
在待求像素的(待插值图的)四邻像素中,将距离待求像素最近的邻像素灰度赋给待求像素。
见下图,设u为待求像素与四邻像素的左上点的水平坐标差,v为待求像素与四邻像素的左上点的垂直坐标差。将待求像素在待插值图中的坐标位置进行四舍五入处理,对应坐标的像素值即为待求像素的值。
优点:
最常见,最通用的算法之一,计算量很小,算法简单,因此运算速度较快。
缺点:
效果不好,放大图像时会出现严重的马赛克,缩小图像则会严重失真。它仅使用离待测采样点最近的像素的灰度值作为该采样点的灰度值,而没考虑其他相邻像素点的影响,因而重新采样后灰度值有明显的不连续性,图像质量损失较大,会产生明显的马赛克和锯齿现象。
Bilinear算法
双线性插值即在两个方向分别进行一次线性插值,通过四个相邻像素插值得到待求像素。
见下图,已知Q11,Q12,Q21,Q22为原图中的四邻像素,P点为待求像素。
图中所示的双线性插值步骤:
(1)通过Q12,Q22线性插值得到R2,通过Q11,Q21线性插值得到R1;
(2)通过R1,R2线性插值得到P.
图中所示的双线性插值先进行了水平方向的插值,再进行垂直方向上的插值,也可以先垂直插值再水平插值。插值方向的顺序不影响最终的结果。
双线性插值的公式为:
f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy
优点:
最常见,最通用的算法之一,效果比最近邻插值法好。计算量较小,运算速度较快。图像连续性较好。双线性插值法效果要好于最近邻插值,只是计算量稍大一些,算法复杂些,程序运行时间也稍长些,但缩放后图像质量高,基本克服了最近邻插值灰度值不连续的特点,因为它考虑了待测采样点周围四个直接邻点对该采样点的相关性影响。
缺点:
放大时图像较为模糊,细节损失较严重。它仅考虑待测样点周围四个直接邻点灰度值的影响, 而未考虑到各邻点间灰度值变化率的影响, 因此具有低通滤波器的性质, 从而导致缩放后图像的高频分量受到损失, 图像边缘在一定程度上变得较为模糊。用此方法缩放后的输出图像与输入图像相比, 存在由于插值函数设计考虑不周而产生的图像质量受损与计算精度不高的问题。
Bicubic算法
在数值分析这个数学分支中,双三次插值(英语:Bicubic interpolation)是二维空间中最常用的插值方法。在这种方法中,函数f在点 (x,y) 的值可以通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。
通过双三次插值可以得到一个连续的插值函数,它的一阶偏导数连续,并且交叉导数处处连续。
双三次插值的计算公式:
双三次插值过程类似于双线性插值,分水平插值和垂直插值两个步骤,但双三次插值涉及的像素数更多(4x4)。
计算系数 的过程依赖于插值数据的特性。如果已知插值函数的导数,常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数h’x与h’y表示 x 与 y 方向的表面斜率,二阶相互导数h’’xy表示同时在 x 与 y 方向的斜率。这些值可以通过分别连续对 x 与 y 向量取微分得到。对于网格单元的每个顶点,将局部坐标(0,0, 1,0, 0,1 和 1,1) 带入这些方程,再解这 16 个方程。
上图公式中的R(x)表示插值采样函数,可以根据需要选择不同的采样函数。常见的有基于三角采样函数、Bell分布采样函数和B样条采样函数。下面介绍这三种常见的双三次插值采样函数。
优点:
立方卷积插值计算量最大,算法也是最为复杂的。在几何运算中,双线性内插法的平滑作用可能会使图像的细节产生退化,在进行放大处理时,这种影响更为明显。在其他应用中,双线性插值的斜率不连续性会产生不希望的结果。立方卷积插值不仅考虑到周围四个直接相邻像素点灰度值的影响,还考虑到它们灰度值变化率的影响。因此克服了最近邻算法和双线性算法的不足之处,能够产生比双线性插值更为平滑的边缘,计算精度很高,处理后的图像像质损失最少,效果是最佳的。
缺点:
立方卷积插值计算量较大,算法相较双线性算法更为复杂。
Lanczos算法
a的典型值是2或3,得到的图像在抗锯齿和保留锐利边缘的效果最佳。下图是a=2和a=3时对应的函数图像。a = 2适合缩小图像,a = 3适合放大图像。类似于双三次插值,对4x4的像素卷积处理,得到待求像素。
优点:
得到的图像在抗锯齿和保留锐利边缘的效果较好。
缺点:
相当于立方卷积插值,计算量较大,算法相较双线性算法更为复杂。
NEDI算法
New Edge-Directed Interpolation,利用局部协方差特性来推导最佳线性MMSE预测的预测系数。由于低分辨率和高分辨率图像在边缘处具有相近的边缘信息,从而可以用低分辨率的协方差特性来得到高分辨率的预测系数。
插值方法:通过4邻域点的值乘上各自的权重值来得到插值点的值(45°或135°方向上的点可看作旋转后的4邻域)
(摘自论文,出处暂时没找到。)
插值过程说明如下:
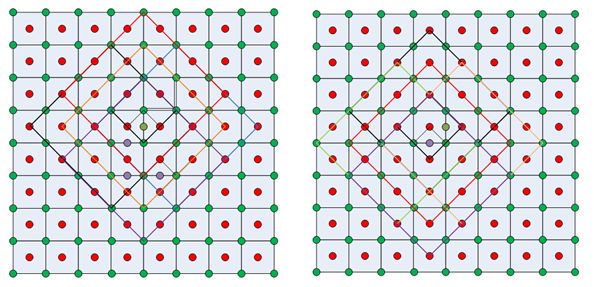
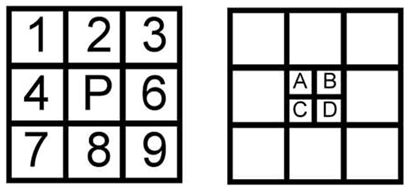
(1)待插值点为O’点(偶行偶列)。图中□ABCD与□A’B’C’D’结构相似,假设它们具有相同的边缘信息。由于O点与A,B,C,D具有某种相关性,则对应地O’点与A’,B’,C’,D’有同样的相关性。因而可以通过求O点和A, B, C, D的协方差来得到A’, B’, C’, D’的权重值,进而插值得到O’的值。
分别以A, B, C, D, O为中心取7x7的矩阵,计算A, B, C, D 与 O 的相关性,得到系数a, 公式为a=inv(C’ *C) *(C’ *r)
其中矩阵C是由以点A, B, C, D为中心的7x7矩阵的像素值组成的, r表示点由以点O为中心的7x7矩阵的像素值组成的。得到的结果a表示A’, B’, C’, D’的权重值。
注意:
这两个条件说明A, B, C, D与O线性无关或处于平坦区域,因而令A’, B’, C’, D’的权重值均为1/4。此外,若计算结果超出0~255的范围,说明计算结果异常,为保证不出现坏点,也令A’, B’, C’, D’的权重值均为1/4.
(2)待插值点为图中的浅绿色点或紫色点(偶行奇列,奇行偶列)。原理同前,矩阵取点方向为逆时针45°。如下图所示,取大小为6x6的框。
优点:
根据统计信息进行插值,细节保持较好。
缺点:
算法复杂,计算量大,运算速度较慢。
EP2X算法
EPX(Eric’s Pixel Expansion)是1992年Eric Johnston为了将SCUMM游戏放大到IBM PC上而设计的。算法具体实现如下所示:
左下图为放大前的像素图,P为放大前的取样像素,ABCD为放大2倍后,取代P的四个子像素。
A = P; B = P; C = P; D = P;
若2, 4的值相同(R/G/B),则A = 2;
若2, 6的值相同(R/G/B),则B = 6;
若4, 8的值相同(R/G/B),则C = 4;
若6, 8的值相同(R/G/B),则D = 8;
若2, 4, 6, 8有三个以上相同,则A = B = C = D = P.
基于EPX的改进算法Eagle:
A = P; B = P; C = P; D = P;
若1, 2, 4的值相同(R/G/B), 则A = 1;
若2, 3, 6的值相同(R/G/B), 则B = 3;
若4, 7, 8的值相同(R/G/B), 则C = 7;
若6, 8, 9的值相同(R/G/B), 则D = 9.
上述EPX 2x和Eagle 2x算法在RGB域已用MATLAB实现,若要对YUV域应用这两种算法,建议仅对Y分量实现。
优点:
算法简单,计算量较小,运算速度较快。边缘保持较好。
缺点:
适用于内容简单的图像,例如UI图,对于情景较为复杂的图像容易产生坏点。
HQX算法
HQX系列算法原理:
通过比较输入图像中的像素点与其8邻域像素点的值,标记邻域点为近或者远(0或1),并使用一个预先生成的查找表格确定输入像素点相应输出的4、9或16个点的合适的权重。其中hq3x算法对斜线具有较好的抗锯齿作用。
下面具体介绍HQ2X算法。
在原图中取如图所示3x3的像素,计算w5和其8邻像素的差的绝对值,大于48则为1,否则为0.
flag = f(w1)<<7 +f(w2)<<6 + f(w3)<<5 + f(w4)<<4 + f(w6)<<3 + f(w7)<< 2 + f(w8)<<1 + f(w9)<<0
易知,flag的取值为0~255.
HQ2X算法里原图中的1个像素映射到目标图中的4个像素——PIXEL00,PIXEL01,PIXEL10,PIXEL11。
插值计算函数有:
Interp1(c1, c2) : ret = (c13 + c2)>>2;
Interp2(c1,c2,c3) : ret = (c12 + c2 + c3)>>2;
Interp3(c1,c2) : ret = (c17 + c2)>>3;
Interp4(c1,c2,c3): ret = (c12 + c27 + c37)>>4;
Interp5(c1,c2) : ret = (c1 + c2)>>1;
Interp6(c1,c2,c3) : ret = (c15 + c22 + c3)>>3;
Interp7(c1,c2,c3) : ret = (c16 + c2 + c3)>>3;
Interp8(c1,c2) : ret = (c15 + c23)>>3;
Interp9(c1,c2,c3) : ret = (c12 + c23 + c33)>>3;
Interp10(c1,c2,c3) : ret = (c1*14 + c2 + c3)>>4.
HQ2X用到了其中的Interp1, Interp2, Interp6, Interp7, Interp9, Interp10.具体算法情况参见C代码,共有161种情况。
优点:
边界清晰,对比度高,细节保持较好。
缺点:
斜边或者有弧度的地方的连续性不好,有明显的锯齿。
Google SR算法
Google SR(即RAISR)的算法原理:
先由LR(low resolution)图像经简单的upscaling得到HR-tmp(high resolution)图像,再用训练得到的滤波模板处理,得到最终的HR图像。
RAISR的MATLAB代码组成部分:training和testing。
Training部分:
(1)已知original HR图,将其长宽均缩小到1/k,再通过cheap upscaling(如bilinear, bicubic等)放大到原尺寸,得到tmp HR图;
(2)在tmp HR图中取固定大小的patch,利用最小二乘法求解出滤波模板H。则可通过tmp HR图估计original HR图中的像素;
, 公式中的Ai指的是tmp HR图像中的patch,h是滤波模板,bi是original HR中相应的像素。直接求此公式的计算复杂度较高,所以转换成如下公式(这里从二维降为一维计算,简化了计算复杂度);
, 其中 ,即将上述公式左乘A的转置。
(3)考虑到patch不同旋转角度的线性滤波模板有所不同,且它们可以统一到一个模板中,故(2)中的A取了patch旋转90°,垂直翻转和中心对称三种情况进行累加计算(MATLAB代码仅有三种,论文中说了四种方向);
(4)计算patch的idx, 根据梯度angle, strength, coherence(与水平和垂直的梯度有关,具体计算参见代码或论文)计算得到(详见代码);
(5)计算当前像素的type,与缩放倍数k有关,type的取值范围是1~k^2,行和列号可被k整除的type为1,在k*k的块内从左到右、从上到下type递增;
(6)将(3)中计算得到的滤波模板h保存到对应的idx, type类中;
(7)对大量图像重复上述步骤。
Testing部分:
(1)已知original HR图,将其长宽均缩小到1/k,再通过cheap upscaling(如bilinear, bicubic等)放大到原尺寸,得到tmp HR图;
(2)在tmp HR图中取固定大小的patch;
(3)计算patch的idx, 根据梯度angle, strength, coherence计算得到(详见代码);
(4)计算当前像素的type;
(5)根据idx和type找到对应的滤波模板,处理tmp HR中的patch;
(6)重复(2)-(5),直到处理完整个tmp HR图,得到RAISR HR图;
(7)计算RAISR HR相对original HR图的PSNR和SSIM值,即为测试结果。
注意:滤波模板是固定倍率的,训练和测试时缩放的倍数一致,应用的时候也只能用于给定的倍率,通常为2倍(论文示例)或3倍(MATLAB代码)。另外,cheap upscaling的算法也应当保持一致。
RAISR的应用过程:
(1)将LR输入图经给定的cheap upscaling算法放大指定倍数k,得到tmp HR图;
(2)在tmp HR图中取固定大小的patch;
(3)计算patch的idx, 根据梯度angle, strength, coherence计算得到(详见代码);
(4)计算当前像素的type;
(5)根据idx和type找到对应的滤波模板,处理tmp HR中的patch;
(6)重复(2)-(5),直到处理完整个tmp HR图,得到RAISR HR输出图。
数学知识:
(1)解线性方程,求特征向量,例如求滤波模板h;
(2)解线性方程,求特征值,例如求梯度angle, strength和coherence。
该算法属于无监督学习算法,没有用损失函数对训练结果进行约束。
优点:
跟bicubic算法相比:细节清晰,轮廓分明,对比度高。主观质量更好。
缺点:
轮廓边缘有明显的伪轮廓;细节丰富的场景中存在坏点;计算量大。