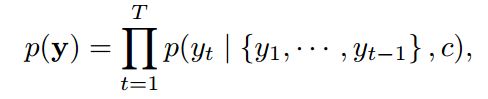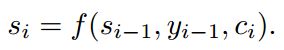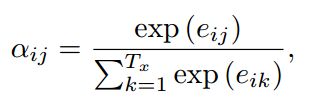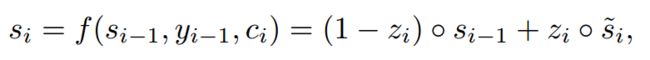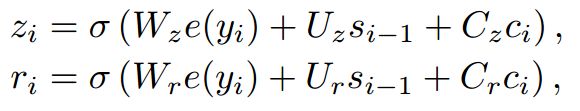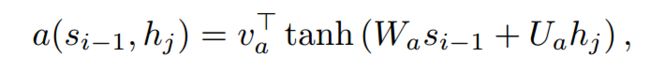论文翻译-通过对齐与翻译联合学习实现机器翻译

1、摘要

基于神经网络的机器学习是目前最为流行的一种机器翻译的方法。与传统的统计学翻译不同，这种翻译方式是通过构建一个神经网络来最大限度提升翻译的性能。该模型是encoder–decoders模型家族中的一种。他使用编码器（encoder）将原始句子编码成一个定长向量，然后使用解码器（decoder）来实现翻译。在本文中，我们推测，在encoder–decoder模型架构下，使用定长向量将是提升翻译性能的瓶颈。为了解决这个瓶颈，我们从原始的句子当中检索最为重要的子句来实施编码解码，而不是通过现在这种硬性分割的方式。通过这种新的方法，在英语到法语的翻译任务中，我们将模型性能提升与state-of-the-artphrase-based 系统相同的水平。此外，性能分析系统还显示，这种软对齐的方式与我们的直观感受非常的契合。

2、神经网络机器翻译的背景知识

从概率学的角度来讲，翻译要做的事情就是在给定原句子 X的情况下，找到能使条件概率P(Y|X)达到最大值的目标句子y。在神经网络翻译中，我们是通过训练一个参数化模型来完成相同的工作。一旦这种条件概率分布被翻译模型学习到，那么我们就可以通过模型对给定的语句进行翻译。

目前，有很多专关于神经网络直接通过训练学习条件概率分布的论文发表。比如（Kalchbrenner and Blunsom, 2013; Cho et al., 2014a; Sutskever et al.,2014; Cho et al., 2014b）神经网络翻译模型有两个最为主要的组件：编码器（encoder）与解码器（decoder），分别负责对原始句子的编码以及对目标句子的解码。有一种典型应用就是将变长的句子首先编码成定长的向量然后在解码成变长的目标语句。

尽管这是一种新的方案，但模型的整体表现还是很优秀的。Sutskever et al. (2014)的这篇论文显示，在英语到法语的翻译工作中。使用lstm单元的rnn翻译模型已经达到了传统的state-of-the-art翻译系统的水平。

2.1 RNN encoder-decoder

首先需要介绍一下模型的基本框架： rnn encoder-decoder，我们在这个框架的基础上来创新性的构建我们的对齐以及翻译模型。在该模型中编码器读取要翻译的句子，该句子是由一组向量序列组成的，可以将其表示为将其编码成一个向量c，这个工作一般是由RNN模型来完成的。我们可以将编码过程表示如下

其中，ht是在时间t的隐藏状态，c是有ht生成的一个定长向量，f，q是非线性函数。

训练解码器的过程主要是在给定表示上下文的向量C以及之前已经预测的所有单词的情况下，预测下一个时间单词 ，可以用下面公式来表示这个过程：

其中 在RNN模型中，该公式还可以表示如下：

在上面的公示的 g是RNN模型训练出来的非线性，多层的模型函数，st是RNN的隐藏状态。

3、训练对齐与翻译

在本章节，我们编写了一种新的模型结构包含给予RNN的编码器与解码器。

3.1 解码器

在这种新的模型结构中，我们将解码器的概率函数做如下定义：

其中si是RNN的隐藏状态可以有下面公式计算得到

需要注意的是，不同于传统编码解码方法，对于目标单词yi是建立在唯一的向量ci基础上的，而每一个ci对于yi不是固定的。

ci表示上下文向量，是由将输入句子映射到隐藏状态然后计算得到。输入句子的每一个单词对于翻译结果的影响程度都涵盖在隐藏状态hi中。在下一节中我们将详细讨论hi的相关计算方法。

ci是有hi与一个权重矩阵点积得到，运算公式如下：

其中可以表示如下：

其中，

eij表示一个对齐模型，该模型表示了，输入句子的第 j 个位置的单词与输出的第 i 个单词的匹配程度。

我们将整个对齐模型参数化成一个前馈的神经网络，这个模型是由其他关键元素联合训练而成。这不同于传统的机器学习翻译系统，将对齐函数作为一个潜在的变量。相反的，对齐模型通过反向传播的梯度下降函数来优化整个模型，而达到一种软对齐的效果。

我们可以这样理解，将所有的标注权重参数求和以获取我们期望的权重参数。而这个权重参数是在整体考虑所有对齐的情况下而得到的一种规律分析结果。假定 为原单词xi到目标单词yi需要对齐的概率，那么第i个上下文向量ci就是这个概率在整个模型中所占的比重。

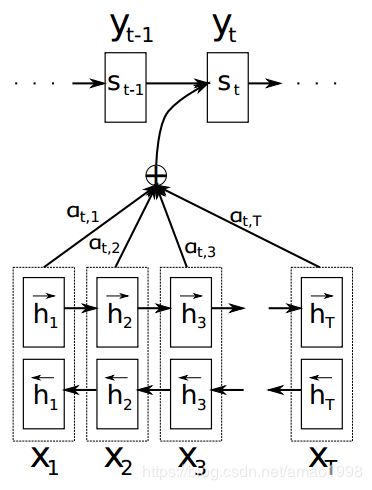
概率值aij与参数eij相关，而eij是反映隐藏变量hj的重要程度。而hj所反映的情况则是通过上一个隐藏状态并生成预测值yi。直观上来讲，这实现了解码器（decoder）的注意力机制，注意力机制通过学习将指导句子的哪一个部分更重要。通过这种注意力机制我们缓解了编码器编码压力，编码器不再需要将整个句子统一编码成一个定长向量。

 

3.2 编码器

编码器就是一个传统RNN模型，该模型首先读入要翻译的句子序列。但是，我们认为当前的单词不光与他之前的单词相关，也与他之后的单词相关，所以这里我们采用了一种双向的RNN的机制。(BiRNN, Schuster and Paliwal, 1997)，双向的RNN模型在语音识别(see, e.g., Graves et al., 2013)的领域已经非常成熟。

双向RNN，包含前向RNN与后向RNN两个基本结构。前向RNN通过句子的原顺序学习前向的隐藏状态序列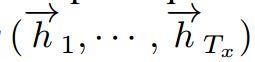，二反向的RNN则倒叙学习另一组状态序列

而最终的隐藏状态变量是由前向与后向两种隐藏状态组合而成，可表示如下：

使用这种及考虑前向又考虑后向的方式，可以通过hj变量充分反应单词以及其周围的词对整体翻译结果的影响。而hj是模型用于计算上下文向量ci的关键因素。

3.3 架构选择

之前的论述是我们对模型的一种理论设计。比如我们用f表示模式的激活函数，用a表示对齐模型。在本节当中，我们将详细讨论在实验中实现该模型的所有细节。

3.3.1 RNN

我们使用隐藏门来作为模型的激活函数，这种门函数在下面论文中有提及Choet al. (2014a)。我们用这种隐藏门来替代简单的双曲正切函数（tanh）。这种门单元的机制与lstm类似，拥有相关的记忆机制。所以在模型中也可以采用lstm单元来替代这种隐藏门。

rnn的一个新的隐藏状态可以通过如下计算获得：

运算符代表矩阵的元素乘积，zi是更新门的输出，这个会在后面消息讨论。计划更新状态可以参考如下公式

e(yi-1)是一个第i-1个单词的m维词向量表示，ri是重置门的输出，当yi是一个1*k的向量表示时，e(yi)是一个m*K矩阵的E中的一列。更新们决定之前状态的多少信息被保留，而充值门则决定之前有多少信息被遗忘或者去除。我们可以使用下面公式计算他们。

而是一个传统的sogmoid激活函数

3.3.2 对齐模型

假如输入句子的序列长度为Tx，输出序列的句子长度为Tx，而对齐模型需要进行Tx*Ty次评估并自我更新。为了减少运算量，我们可以采用如下计算方式。

其中，Wa，Ua，Va都是模型参数矩阵。由于与i无关，所以可以提前计算获得