第四章 Dijkstra和A*寻路算法
寻路
寻路希望ai中的角色能够计算一条从当前位置到目标位置合适的路径,并且这条路径能够尽可能的合理和短。
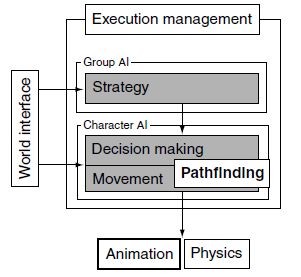
在我们的ai模型中,寻路在决策和移动之间。游戏中大多数寻路的实现是基于a星算法,但是它不能直接使用关卡数据工作,需要转换成特别的数据结构:有向非负权重图。除了a星算法本章也将介绍最短路径算法,它是一个更简单版本的a星算法,但是更常用于决策。
4.1 寻路图
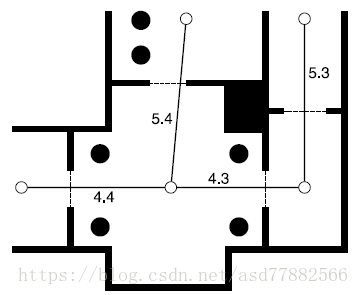
图是一个数学概念,有两种元素组成:节点,通常由点或者圈表示,在游戏关卡中表示一个区域;线:连接两个节点,表示可通过。
权重图在图的基础上,在每条线上加了一个数字值,在数学图论中被称作权重,而在游戏中它通常被称作花费(cost)。
寻路图中的花费(cost)通常代表时间或者距离。不过也可能是时间和距离的混合或者其他因素。
区域的节点
我们期望测量每个区域连接之间的距离或者时间,所以我们以每个区域的中心作为节点。如果区域很大,那么两个区域之间的距离就会更大,对应花费也更大。
非负约束: 在游戏中,两个区域之间的花费一般不会出现负数的情况,所以对于权重我们限制为非负值。
4.1.3有向权重图
在游戏开发中,很多情况下我们从一个区域A能够进入区域B,反过来并不一定成立,或者从A到B和从B到A的花费并不相同。所以使用有向图假设连接只有一个方向。
4.1.5 描述(Representation)
在寻路算法中图结构如下所示:
class Graph:
# 返回所有以传入点为起点的连接
def getConnections(fromNode)
class Connection:
def getCost()
def getFromNode()
def getToNode()根据不同的需求,Connection里边的cost可以是一个确定的值,也可以在需要获取的时候才计算。
上边并没有node的结构,我们通常以一个数字索引表示。
4.2 最短路径算法(Dijkstra)
Dijkstra算法最初被设计出来并不是作为游戏中的寻路使用,而是为了解决数学图论中的一个问题,被称作“最短路径”。
游戏中的寻路有一个起始点和目标点,最短路径算法被设计找出从起始点到任意其他位置的最短路径,而目标点也在结果中。所以如果我们只想找出起始点到目标点的最短路径,这个算法会丢弃许多其他目标点的路径而导致浪费。
由于这个问题,我们不会在主要的寻路算法中使用它。而它更常用于战术解析(在第六章战术和策略ai中)
4.2.1 解决的问题
给出一个有向非负权重图和图中的两个节点(分别作为起始点和目标点),计算出所有可以从起始点到目标点总路径发费最少的一条路径。
可能有多个权重在最小值的路径,我们只需要其中任意一条,并且不在乎是那条。
路径由一组连线组成。
4.2.2 算法介绍
通俗的说,Dijkstra从开始点向它的连接线扩散。随着它向更远的节点扩散,它记录来自的方向(想象在黑板上画箭头表示回到起点的路径)。最终将抵达目标点并根据箭头返回到开始点来生成完整的路径。由于Dijkstra调节扩散的进程,它保证箭头总能以最短路径指回开始点。
用更多细节来描述。Dijkstra迭代执行。每一次迭代它考虑图中的一个节点并且跟随以它扩散的连接。第一次迭代考虑的是起始点。在连续的迭代中它选取一个节点执行后边我们讨论的算法。我们称每次迭代的节点为“当前节点”。
执行当前节点
迭代期间,Dijkstra考虑每一个以当前节点出去的连线。针对每一条连线找出结束节点并存储它到目前为止路径的总花费(我们成为“cost-so-far”)。
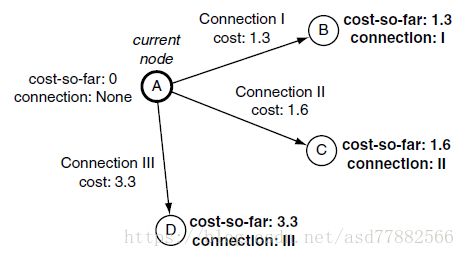
第一次迭代,开始点是当前节点,对应连线的结束节点的cost-so-far为连线花费。下图展示了第一次迭代之后的情况。
第一次迭代之后,每一条连线的结束节点的cost-so-far是连线的花费加上当前节点的cost-so-far,如下图示:
在算法的实现上,第一次和之后的遍历没有区别,通过设置开始节点的cost-so-far为0,我们可以用同一块代码执行所有遍历。
节点列表
算法将所有遇到过的节点放置在两个列表中:open和closed。在open列表中记录了所有已经遇到过但是还没有作为当前节点遍历过的的节点。已经遍历过的节点放置在closed列表中。开始的时候,open列表只有一个开始节点,closed列表为空。
每一次迭代,算法从open列表中选择cost-so-far最小的节点。然后作为当前节点执行算法,并从open列表中移除该节点放入closed列表中。
但是也有一个不同,我们考虑当前节点的每一条连接的结束节点并不一定都是未发现节点。也有可能处于open列表或者closed列表中,这是处理它们会有一些不同。
计算open和closed列表节点的cost-so-far
如果我们在遍历中计算的连线结束点已经存在与open或者closed列表中,那么这个点已经有了cost-so-far值和抵达该点的连接记录。这时候是否重新修改记录信息就要依据新的cost-so-far是否比原值小。
需要更新节点信息的话,这个节点需要被放置于open列表中,如果它已经在closed列表中,需要从中移除。
严格的说,Dijkstra算法不会对一个在closed列表的节点找出一个更好的路径,所以如果节点在closed列表中我们不必再做cost-so-far比较。然而A星算法并不是这样,无论是否在closed列表中,我们都要做比较判定。
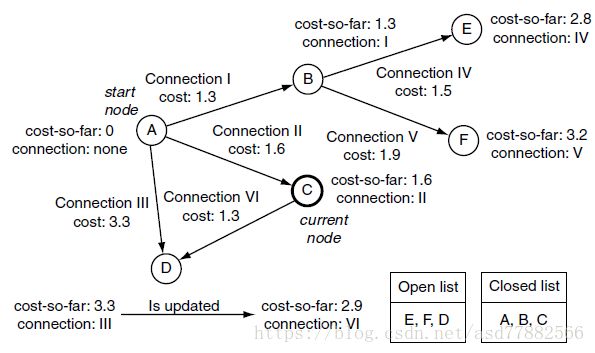
下图展示了open节点的信息更新,新的路径,通过节点C更快速所以节点D的信息进行了更新:
算法结束
标准的Dijkstra算法在open列表为空时结束,即已经考虑了从开始节点延伸的所有节点,并且它们都处于了closed列表中。
对于寻路,我们只关心是否抵达目标节点。然而,只有在目标节点在open列表中cost-so-far最小的时候(即执行完目标点要放入closed列表中时)才应该结束。考虑到上图,如果目标点时D,在对A点进行操作时,D点已经被放置于open列表中,但是实际上当前路径A-D并不是最近路径。在执行到C点,此时处于open列表的有E,F,D,这个时候D才找到了最短路径。
在实际应用中,这个规则经常被打破,第一次发现目标节点的路径常常是最短路径,即使不是最短的通常也不会差距太大。基于这种情况,很对开发者实现的寻路算法中一旦遇到目标节点,便立即结束寻路,而不是直到它从open列表中被选取执行的时候才作为结束。
检索路径
最后一个阶段是检索路径。我们冲目标点开始,查询它的连线找到上一个开始节点,再往回遍历最终回到了开始点,能够得到一个从目标点到开始点的最短路径,颠倒改路径可以得到最终结果。
4.2.3 伪代码
def pathfindDijkstra(graph, start, end):
# 这个结构存储了已经执行过的节点信息
struct NodeRecord:
node
connection
costSoFar
# 初始化开始节点记录
startRecord = new NodeRecord()
startRecord.node = start
startRecord.connection = None
startRecord.costSoFar = 0
# 初始化open和closed列表
open = PathfindingList()
open += startRecord
closed = PathfindingList()
while length(open) > 0:
current = open.smallestElement()
if current.node == goal: break
connections = graph.getConnections(current)
for connection in connections:
endNode = connection.getToNode()
endNodeCost = current.costSoFar + connection.getCost()
# 已经在closed列表中,不再考虑
if closed.contains(endNode): continue
else if open.contains(endNode):
endNodeRecord = open.find(endNode)
# 不需要更新数据
if endNodeRecord.cost <= endNodeCost:
continue
else:
endNodeRecord = new NodeRecord()
endNodeRecord.node = endNode
endNodeRecord.cost = endNodeCost
endNodeRecord.connection = connection
if not open.contains(endNode):
open += endNodeRecord
open -= current
closed += current
if current.node != goal: # 未发现目标点
return None
else:
path = []
while current.node != start:
path += current.connection
current = current.connection.getFromNode()
return reverse(path)
class Connection:
cost
fromNode
toNode
def getCost(): return cost
def getFromNode(): return fromNode
def getToNode(): return toNode4.2.6 弱点
Dijkstar算法无差别的遍历当前最短路径,对于查找起始点到任意点的最短路径该算法很有效,但是对于点对点的路径查找很浪费。
4.3 A*
游戏中的寻路同义与A*算法。A *算法很容易实现,有效并且有很多优化的能力。过去10年提及过的每一个寻路系统都将一些A星算法的变种作为它的关键算法,而且A星算法在寻路之外也有很好的应用。第五章我们将看到A星应用于计划角色复杂的一系列动作。
A星被设计用于解决点对点寻路而不是用来解决图论中的最短路径问题。它可以被扩展来解决更复杂的问题,但是最终总是返回一个从起始点到目标点的一条路径。
4.3.1 解决的问题
A星解决的问题和最短路径寻路算法一致。
4.3.2 算法解析
总的来说,A星算法和Dijkstra一样的方式工作,但是不是在open列表中选取最小的cost-so-far节点,而是选取以更可能短距离到达目标点的节点。“更可能”通过一个启发式方法来操作。如果这个启发式方法很精确,那么A星算法就会很有效,如果很糟糕,那么算法的性能将会比Dijkstra更差。
处理当前节点
在一次迭代中,A星对以当前节点开始的每一条连接,找到对应结束点并存储它的cost-so-far和这条连接,到这里和Dikstra一致。此外,节点多存储了一个值:从开始节点通过该节点到目标点的总预估花费(称作estimated-total-cost)。这个预估值是两个值的和:cost-so-far和当前点到目标点的花费。
这个预估值被称作节点的启发值(heuristic value),为非负数。生成启发值是A星算法的关键点。
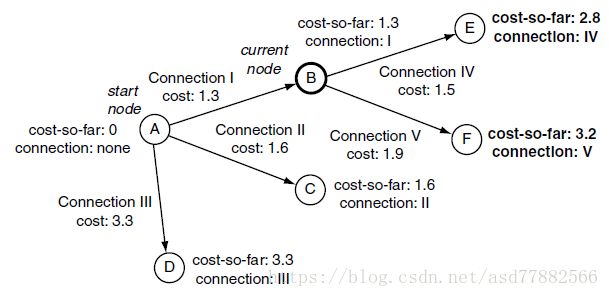
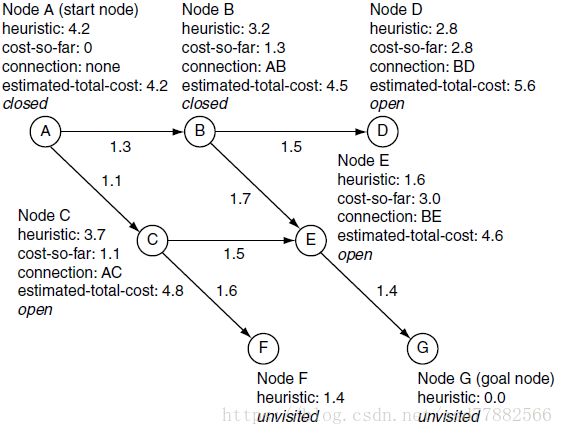
下图展示了A*算法中启发值的计算:
节点列表
和Dijkstra一样,算法也是用了open列表存储已看到但未处理的节点,closed列表存储已处理节点。不同之处是,每次从open列表中选取最小预估总发费的节点作为当前节点。
如果当前节点有更小的预估总发费,就意味着它有相对更小的cost-so-far和到目标点的预估值。如果预估是准确的,则更靠近目标点的节点优先考虑,缩小搜寻的范围到一个更有利的区域。
计算open和closed节点的cost-so-far
和Dijkstra一样,我们在遍历中会修改open和closed节点的记录值,计算出节点cost-so-far的值,如果节点记录已经存在并且存储的cost-so-far大于最新值,就更新它。
和Dijkstra不一样的是,A星算法会对已经在closed列表的节点发现更好的路线(即更小的总预估花费),此时需要更新此节点记录并移至open列表中,这样当下次该节点重新作为当前节点时,会重新计算对应连接的结束点的值。
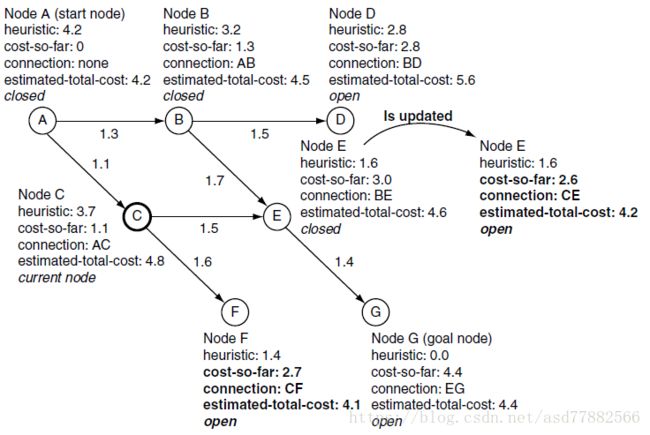
如下图示:
算法结束
在很多实现中,A星算法会在发现open列表里预估总花费节点为目标节点时结束。
但是基于上边我们讨论到的,即使节点有了最小预估总值,在之后的迭代中还是可能会更新这个值,所以这种结束方法并不能保证能够找到最短路径。
为了保证我们能够获取到最短路径,我们需要保持和Dijkstra一样,只有在open列表中cost-so-far最小的节点为目标节点时才结束算法。但是这些额外的检测会使算法运算更长而降低了A星算法的性能。
A星实现理论上不会得到最优结果,不过我们可以通过启发函数控制。依赖于启发函数的选择,我们可以做到获取最优解或者获得次优解但是运算速度更快。之后会讨论到启发函数的影响。
由于A星算法经常只得到次优结果(flirts with sub-optimal results),很多A星实现中在发现目标节点时就结束而不再确保是open列表的最小值。
4.3.3 伪代码
def pathfindAStar(graph, start, end, heuristic):
struct NodeRecord:
node
connection
costSoFar
estimatedTotalCost
startRecord = new NodeRecord()
startRecord.node = start
startRecord.connection = None
startRecord.costSoFar = 0
startRecord.estimatedTotalCost = heuristic.estimate(start)
open = PathfindingList()
open += startRecord
closed = PathfindingList()
while length(open) > 0:
# 找到open列表的最小预估总值
current = open.smallestElement()
if current.node == goal: break
connections = graph.getConnections(current)
for connection in connections:
endNode = connection.getToNode()
endNodeCost = current.costSoFar + connection.getCost()
if closed.contains(endNode):
endNodeRecord = closed.find(endNode)
if endNodeRecord.costSoFar <= endNodeCost:
continue
# 节点更新了记录值,要重新移到open列表中
closed -= endNodeRecord
# 通过这种方式获取结束节点到目标点的预估值
endNodeHeuristic = endNodeRecord.cost - endNodeRecord.costSoFar
else if open.contains(endNode):
endNodeRecord = open.find(endNode)
if endNodeRecord.costSoFar <= endNodeCost:
continue
endNodeHeuristic = endNodeRecord.cost - endNodeRecord.costSoFar
else: # 处于未访问状态,加入到open列表中
endNodeRecord = new NodeRecord()
endNodeRecord.node = endNode
# 使用启发函数计算当前节点到目标点的预估值
endNodeHeuristic = heuristic.estimate(endNode)
endNodeRecord.cost = endNodeCost
endNodeRecord.connection = connection
endNodeRecord.estimatedTotalCost = endNodeCost + endNodeHeuristic
if not open.contains(endNode):
open += endNodeRecord
open -= current
closed += current
if current.Node != goal: # 未找到有效路线
return None
else:
path = []
while current.node != start:
path += current.connection
current = current.connection.getFromNode()
return reverse(path)4.3.4 数据结构和接口
open和closed存储列表结构的实现略…
启发函数
启发方法通常作为一个函数讨论,它也实现成一个函数。在上边的伪代码中我们实现为一个对象,它存储了当前的目标节点:
class golaNode:
def Heuristic(goal): goalNode = goal
def estimate(node)寻路时使用方式如下:
pathfindAStar(graph, start, end, new Heuristic(end))启发方法速度
启发方法在循环中处于最低点(called at the lowest point),因为它需要进行预估,可能需要执行一些算法计算。如果比较复杂的话,会拖慢整个寻路算法执行。
一些情况下可能允许通过建立一个启发值的查找表来优化,但是大多数情况下大量的点对点组合会导致表变得巨大无比。
对寻路中的启发函数进行优化是很有必要的,之后会对此进行探讨。
4.3.7 节点数组A星(Node Array A*)
节点数组A*是一个比普通A星算法更快的长松A星算法。
使用一个节点数组
我们可以做一个权衡增加内存使用来提高执行速度。在算法开始之前,我们创建一个数组用来存储图中每一个节点的记录。节点被标记为一个连续的数字,我们不需要再在两个列表中查找节点的信息,直接可以在节点数组中找到。
判断一个节点是否在open或closed列表中
在最初的算法中,需要查找两个列表,检查节点是否已经在里边,这会导致速度变慢,为了解决找出节点在哪个列表的问题,我们可以在节点记录中加入一个额外信息,它表示当前节点处于那个状态(unvisited, open, closed),如下示:
struct NodeRecord:
node
conneection
costSoFar
estimatedTotalCost
category # 一个数字指示不同状态closed列表不再需要
由于我们提前创建了所有节点的记录,而closed列表的唯一作用是为了判断节点是否在里边(处于closed状态),根据上边的修改closed列表不再需要。
open列表的实现
我们仍需要判断所有open列表中花费最小的节点,所以仍然需要一个用于排序的open列表存在。
大图的一个变种
如果图非常大,那么提前创建所有节点会造成很大的浪费。我们可以将节点数组改为检点数组指针,只有当发现节点的时候,才会创建节点记录对象,然后将它存入节点指针数组,如果在查找这个数组时发现对应记录是空指针,说明该节点是一个未发现的状态。
4.3.8 选择启发方法
启发散发越精确,A星迭代的越少,执行得就越快。如果可以有一个完美的启发算法(总是能够获得两个节点最小路径的距离),A星将直接获得最优解:算法只需要P次迭代,P是最短路径的路线数。
不幸的是,最优启发方法本身就是寻路算法要解决的问题,所以实际上启发方法在很少情况下会是准确的。
对于不完美的启发算法,它预估的高或低会使A星算法表现得明显不一样。
低估的启发方法
如果启发方法太低,即预估低于真实的路径长度,A*算法将花费更多的执行次数。因为预估总发费会偏向于cost-so-far值,所以A星算法在open列表中偏向于选择更靠近开始点的节点,而不是更靠近目标点。
如果启发方法在任何情况下都低估时,A星算法将产生一个最好的路线结果。和Dijkstra算法产生一样的路线。最极端的情况,启发方法每次都返回0,则A*将变成Dijkstra算法。如果启发方法一旦高估过,那么就不再能保证。
在大多数效果最重要的应用中,确保启发方法低估是很重要的。大多数学术和商业的寻路文章,精度很重要,所以低估的启发方法比比皆是。这个情况也会影响到游戏开发者。在应用中,不要完全抵制高估的期发方法,游戏不是需要最优精度,而是需要更可信的结果。
高估的启发方法
如果启发方法太高,那么将高估真实的路径长度,A星算法可能不会返回最好路线。算法将倾向于生成更少路径点的路线,即使花费更大。
总预估花费将偏向于启发方法。A星算法将更少的关注cost-so-far的值并且偏向于距目标更少距离的节点。这将更快的搜寻到目标点,但是更可能错过最好的路线。
高估的启发方法通常被称作“不允许的启发”,不是说不能够使用它,而是算法通常不会获得最短路线。高估如果几乎很完美的话可以使A星算法执行的更快,因为它倾向更快抵达目标。如果只是轻微的高估,通常也会返回最好路线。
欧几里得距离(Euclidean Distance)
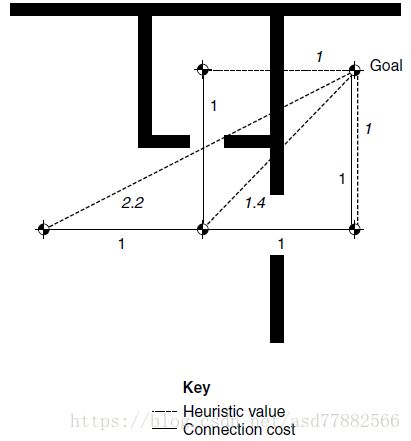
在通常以考虑距离的寻路问题中,一个常见的启发方法是欧几里得距离,它保证低估于真实值。它指的是两个节点之间的直线距离,不考虑是否会通过墙或障碍物。
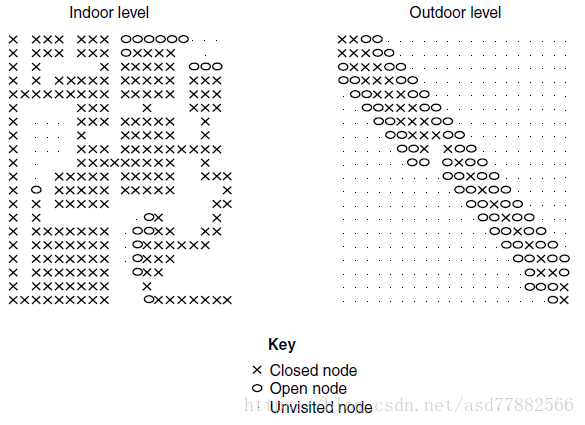
下图所示在一个室内场景的欧几里得距离示例,由于直线距离是两点最短距离,所以欧几里得距离总是低估或者精确。
在室外中,有更少的障碍来限制移动,欧几里得距离会更加精确并提供更快的寻路。
下图展示了基于瓦片的室内和室外关卡可视化的寻路情况,使用欧几里得距离启发方法,室内性能很差,而室外遍历的节点更少,新能更好。
集群启发方法(Cluster Heuristic)
集群启发方法通过将一组节点作为一个集合来工作。在同一个集合的节点代表关卡中一个联通的区域。集群可以通过本书后边提到的图聚类(graph clustering)算法自动生成。通常是手工或者通过关卡设计产生。
需要一个查找表来保存每一对集群的最短距离。这是一个离线运算。选择一个足够小的群集集合这样算法会在一个合理的时间帧完成并且存储在在一个合理的内存大小中。
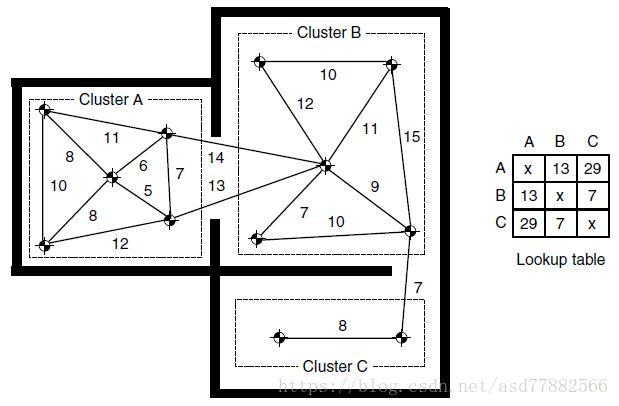
当该启发方法在游戏中,如果开始和结束节点在同一个集群中,直接使用欧几里得距离(或者其他方式)产生结果。否则预估值直接在查找表中获取。如下图所示,图中的每一个连接的两个方向有同样的花费:
这里有一个问题,由于同一群集里的所有节点有相同的预估值,A星算法不能够找到通过一个集群的最好路线。当算法移动到下一个集群之前当前集群节点可能机会要完全迭代一遍。
如果每个集群的大小很小,那么他就不是一个问题,启发方法的精确性会很好。另一方面查找表也会变得很大(因为相应的集群数量会很多)。
如果每个集群的大小太大,那个将有一个很差的性能表现,一个更简单的启发方法会是个更好的选择。
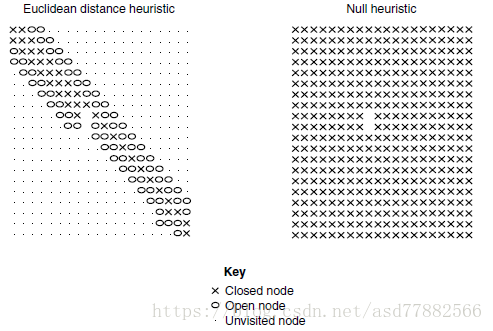
A星中的填充模式
下图展示了在基于瓦片的室内关卡A星算法使用不同启发方法的查找表现,null意味着启发方法每次都返回0:
这是一个信息和搜索权衡的一个很好的示例。
如果启发方法更加复杂并且对游戏关卡特殊定制,那么A星算法搜寻的更少。启发方法提供极限的信息进行极限扩展:完全精确的预估,将产生A星最优性能。
另一方面,欧几里得距离提供了更少的信息,只知道两点间的距离,这些信息仍然需要算法做更多的搜索。
而返回0的启发方法没有任何信息,需要最多的搜索。
在室内地图例子中,有大量障碍物,欧几里得距离不是表现真实距离的最好方法。在室外地图中,如下图所示,有更少的障碍,此时欧几里得距离更加的精确和快速,而集群启发方法并不能提升性能(甚至降低性能):
启发方法的质量
制作一个启发方法更像是一门艺术而不是科学。它的意义被ai开发者低估了。在我们的经验中,很多开发者只是使用一个欧几里得距离方法而不考虑最佳方法。
选取一个最佳启发方法的得体方式是可视化算法的迭代过程,可以在游戏中显示或者在测试之后显示输出结果。这样可以发现我们原本认为有效的启发方法一些弱点。