算法与数据结构-二叉树的基本操作C语言实现
序言
二叉树这部分当时学习C语言的时候就没有特别重视,现在遇到这类题就比较头疼,所以需要重新复习一下。
二叉树的基本操作包括哪些
二叉树的建立
- 逐个结点输入
- 广义表方式输入
广义表方式输出二叉树
二叉树的销毁
求二叉树的深度
二叉树的遍历
统计二叉树的结点数
统计二叉树的叶子结点数
交换左右子树
复制二叉树
查找某一结点
删除二叉树的某一结点
1. 二叉树的定义
typedef ElemType char; //自定义数据域类型
struct BinaryTree
{
ElemType data; //数据域
struct BinaryTree *lchild; //左子树
struct BinaryTree *rchild; //右子树
};
typedef struct BinaryTree TreeNode; //给结构体struct BinaryTree取个别名叫TreeNode
typedef struct BinaryTree * BiTree; //给结构体指针struct BinaryTree *取个别名叫BiTree
//初始化
void IniBTree(BiTree BT)
{
BT = NULL;
return;
}
2. 二叉树的建立
- 方法1:逐个结点输入
/* 先序创建二叉树:根结点 -> 左子树 -> 右子树 */
void CreateBTree(BiTree BT)
{
char ch;
ch = getchar(); //头文件,相当于scanf("%c", &ch)
if (ch == ' ')
BT = NULL;
else
{
if(! (BT = (BiTree)malloc(sizeof(TreeNode))))
exit(1);
BT -> data = ch; //生成根节点
BT -> lchild = NULL; //构造左子树
BT -> rchild = NULL; //构造右子树
CreateBiTree(BT -> lchild);
CreateBiTree(BT -> rchild);
}
}- 方法2:利用广义表建立二叉树
- 即根据广义表 A(B(C,D),E(,F(G)))的输入,建立二叉树
int StackMaxSize = 3;
void CreateBTreeWithGenList(BiTree BT, char *string)
{
BiTree TempNode;
Bitree s[StackMaxSize]; //定义数组为存储各结点的指针的栈
int top = -1; //栈顶指针,初始值为-1
int branchValue; //分支值,作为处理结点的标志,1表示处理左子树,2表示处理右子树
int i = 0; //数组计数元素
//原二叉树初始化
BT = NULL;
//开始读入广义表字符串
while (string[i])
{
switch(string[i])
{
case ' ': break;
case '(':
{
if (top == StackMaxSize - 1)
{
printf("栈空间太小,需要增大栈空间!\n");
exit(1);
}
top++;
s[top] = TempNode;
k = 1; //切换到左子树
break;
}
case ')':
{
if (top == -1)
{
printf("二叉树广义表字符串错误\n");
exit(1);
}
top--;
}
case ',': k = 2; break; //切换到右子树
default: //默认情况下,即读取到字母字符,对应赋值。
{
TempNode = (BiTree)malloc(sizeof(TreeNode));
TempNode -> data = string[i]; //临时结点赋值
TempNode -> lchild = TempNode -> rchild = NULL;
if (BT == NULL)
BT = TempNode; //根节点赋值
else
{
if (k == 1)
s[top] -> lchild = TempNode;
else
s[top] -> rchild = TempNode;
}
}
} //switch结束
i++;
} //while结束
}3. 广义表方式输出二叉树
void PrintBTreeWithGenList(BiTree BT)
{
if (BT)
{
printf("%c", BT -> data);
if (BT -> lchild || BT -> rchild)
{
printf("(");
PrintBTreeWithGenList(BT -> lchild);
if (BT -> rchild)
{
printf(",");
PrintBTreeWithGenList(BT -> rchild);
}
printf(")");
}
}
}4. 二叉树的销毁
void DestroyBTree(BiTree BT)
{
if (BT)
{
DestroyBTree(BT -> lchild);
DestroyBTree(BT -> rchild);
free(BT);
BT == NULL;
}
}5. 检查二叉树是否为空
int BTreeEmpty(BiTree BT)
{
if (BT == NULL)
return 1;
else
return 0;
}6. 求二叉树的深度
//递归方式计算二叉树的深度,每一层的深度都能够得到比较
int BTreeDepth(BiTree BT)
{
if (BT == NULL)
return 0;
else
{
int depth1 = BTreeDepth(BT -> lchild); //计算左子树的深度
int depth2 = BTreeDepth(BT -> rchild); //计算右子树的深度
if (depth1 > depth2)
return depth1 + 1;
else
return depth2 + 1;
}
}
//或递归方式求二叉树的深度
int BTreeDepth(BiTree BT)
{
if (BT == NULL)
return 0;
else
{
int ldepth = BTreeDepth(BT -> lchild);
int rdepth = BTreeDepth(BT -> rchild);
}
return (ldepth > rdepth) ? (ldepth + 1) : (rdepth + 1);
}
7. 二叉树的遍历
/* 前序遍历:根节点 -> 左子树 -> 右子树 */
void PreOrderTraverse(const BiTree BT)
{
if (!BT)
return;
//遍历
printf("%c ", BT -> data); //根节点
PreOrderTraverse(BT -> lchild);
PreOrderTraverse(BT -> rchild);
}
/* 中序遍历:左子树 -> 根节点 -> 右子树 */
void InOrderTraverse(const BiTree BT)
{
if (!BT)
return;
//遍历
InOrderTraverse(BT -> lchild);
printf("%c ", BT -> data); //根节点
InOrderTraverse(BT -> rchild);
}
/* 后序遍历:左子树 -> 右子树 -> 根节点 */
void PostOrderTraverse(const BiTree BT)
{
if (!BT)
return;
//遍历
PostOrderTraverse(BT -> lchild);
PostOrderTraverse(BT -> rchild);
printf("%c ", BT -> data); //根节点
}
/* 层序遍历:逐层从左到右 */
void LevelOrderTraverse(BiTree BT)
{
BiTree temp;
BiTree queue[QueueMaxSize]; //定义队列所使用的数组,元素类型为指向结点的指针类型
int front = 0;
int rear = 0;
if (BT != NULL) //根结点入队
{
queue[rear] = BT;
rear = (rear + 1) % QueueMaxSize;
}
while (front != rear)
{
temp = queue[front];
front = (front + 1) % QueueMaxSize;
printf("%c ", temp -> data);
if (temp -> lchild != NULL) //输出结点存在左子树
{
queue[rear] = temp -> lchild;
rear = (rear + 1) % QueueMaxSize;
}
if (temp -> rchild != NULL)
{
queue[rear] = temp -> rchild;
rear = (rear + 1) % QueueMaxSize;
}
}
}
//1. 层序遍历需要使用一个队列,开始把整个树的根结点入队,然后每从队列中删除一个结点并输出该结点时,都把它的非空的左右孩子入队,当队列为空时算法结束。
//2. 算法中,队列的最大长度不会超过二叉树中相邻的两层的最大结点数,所以提前在程序开始处定义最大队列长度QueueMaxSize大于队列的最大长度,就无需考虑队列溢出的问题了
8. 统计二叉树的结点数
/* 二叉树的结点数 = 左子树 + 右子树 + 1 */
int BTreeNodeCount(BiTree BT)
{
if (BT == NULL)
return 0;
else
return BTreeNodeCount(BT -> lchild) + BTreeNodeCount(BT -> rchild) + 1;
}
9. 统计二叉树的叶子结点数
/* 叶子结点:没有左右子树的结点 */
int BTreeLeafCount(BiTree BT)
{
if (BT == NULL)
return 0;
if (BT -> lchild == NULL && BT -> rchild == NULL)
return 1;
//递归实现
return BTreeLeafCount(BT -> lchild) + BTreeLeafCount(BT -> rchlid);
}10. 统计二叉树度为1的结点
/* 统计二叉树的度为1的结点个数 */
//度:一个结点的子结点的个数
int Degree1Count(BiTree BT)
{
if(!BT)
return 0;
if ((!BT -> lchild && BT -> rchild) || (BT -> lchild && !BT -> rchild))
return 1;
else
return Degree1Count(BT -> lchild) + Degree1Count(BT -> rchild);
}11. 交换左右子树
/* 相当于对称翻转,递归实现 */
void ExchangeChildTree(BiTree BT)
{
if (BT)
{
BiTree Temp = NULL;
if (BT -> lchild || BT -> rchild)
{
ExchangeChildTree(BT -> lchild);
ExchangeChildTree(BT -> rchild);
Temp = BT -> lchild;
BT -> lchild = BT -> rchild;
BT -> rchild = Temp;
}
}
}12. 复制二叉树
/* 递归实现 */
BiTree CopyBTree(BiTree BT)
{
BiTree P, lchild, rchild;
if (BT == NULL)
return;
lchild = CopyBTree(BT -> lchild);
rchild = CopyBTree(BT -> rchild);
P = (BiTree)malloc(sizeof(struct BinaryTree));
P -> data = BT -> data;
P -> lchild = lchild;
P -> rchild = rchild;
return P;
}13. 查找某一结点
/* 查找某一结点:查找成功返回结点位置,失败返回NULL */
BiTree* FindBTree(BiTree BT, ElemType x)
{
if (BT == NULL)
return NULL;
else //递归查找
{
if (x == BT -> data)
return BT;
else
{
ElemType* p;
if (p = FindBTree(BT -> lchild, x))
return p;
if (p = FindBTree(BT -> rchild, x))
return p;
return NULL;
}
}
}
14. 删除二叉树的某一结点
- 说明:二叉树删除结点有三种情况
- [1] 该结点没有子结点:直接删除,并修改其父结点
- [2] 该结点只有一个子结点:将该结点的子结点直接提升至该结点处,并修改相应的指针
- [3] 若该z结点有两个子结点:找到z结点的中序后继结点y,并用y的右子树替换y结点,y结点替换z结点,z的左子树置为y的左子树。如下图所示
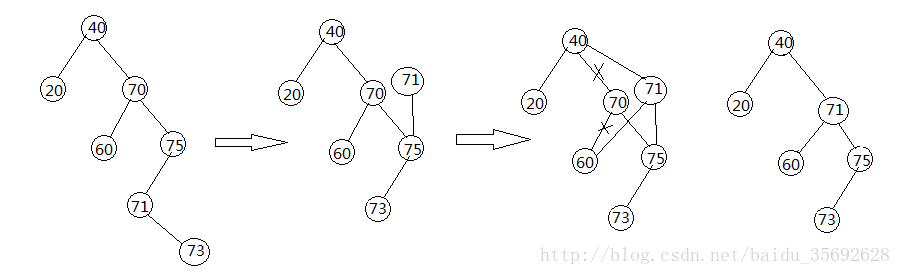
//此时的二叉树结构体定义修改为
typedef ElemType char; //自定义数据域类型
struct BinaryTree
{
ElemType data; //数据域
struct BinaryTree *prev; //前驱结点,该指针的目的是为了方便找到父结点
struct BinaryTree *lchild; //左子树
struct BinaryTree *rchild; //右子树
};
typedef struct BinaryTree *BiTree;
//删除某一结点方式:先找到后删除
int DeleteBTreeNode(BiTree BT, ElemType x)
{
//查找到该元素所在的结点位置,返回结点指针!
BiTree temp = FindBTree(BT, x);
if (temp == NULL)
return 0;
//1. 没有子结点
if (temp -> lchild == NULL && temp -> rchild == NULL)
{
if (temp -> prev -> lchild == temp) //如果是父结点的左子树
temp -> prev -> lchild = NULL;
else
temp -> prev -> rchild = NULL;
free(temp);
}
//2. 只有左子树
if (temp -> rchild == NULL)
{
if (temp -> prev -> lchild == temp) //如果是父结点的左子树
temp -> prev -> lchild = temp -> lchild;
else
temp -> prev -> rchild = temp -> lchild;
free (temp);
}
//3. 只有右子树
if (temp -> lchild == NULL)
{
if (temp -> prev -> lchild == temp) //如果是父结点的左子树
temp -> prev -> lchild = temp -> rchild;
else
temp -> prev -> rchild = temp -> rchild;
free (temp);
}
//4. 既有左子树又有右子树
else
{
BiTree y = temp -> rchild; //寻找中序后继结点y,即temp结点右子树的最左子树
while (y -> lchild != NULL)
y = y -> lchild;
if (y == temp -> rchild) //y是要删结点的右子树
{
//判断要删结点是其父结点的左子树还是右子树
if (temp -> prev -> lchild == temp) //左子树
{
temp -> prev -> lchild = y;
y -> lchild = temp -> lchild;
temp -> lchild -> prev = y;
}
else
{
temp -> prev -> rchild = y;
y -> lchild = temp -> lchild;
temp -> lchild -> prev = y;
}
}
else
{
y -> prev -> lchild = y -> rchild; //注意y的右子树可能不存在
//同上。判断要删除结点是其父结点的左子树还是右子树
if (temp -> prev -> lchild == temp) //左子树
{
temp -> prev -> lchild = y;
y -> lchild = temp -> lchild;
y -> rchild = temp -> rchild;
temp -> lchild -> prev = y;
temp -> rchild -> prev = y;
}
else
{
temp -> prev -> rchild = y;
y -> lchild = temp -> lchild;
y -> rchild = temp -> rchild;
temp -> lchild -> prev = y;
temp -> rchild -> prev = y;
}
}
free (temp);
}
return 1;
}
//注:为避免冗长,可将上述判断左右子树及结点替换的部分单独写一个函数实现。Acknowledgements:
http://blog.csdn.net/sysu_arui/article/details/7865876
http://blog.csdn.net/wtfmonking/article/details/17038077(推荐)
http://blog.csdn.net/lub0807/article/details/37969059
http://blog.csdn.net/nzh1234/article/details/31076401
http://blog.csdn.net/heart_love/article/details/50943089
2017.08.20