图像缩放--插值法(opencv,原理)
第一部分:
在做数字图像处理时,经常会碰到小数象素坐标的取值问题,这时就需要依据邻近象素的值来对该坐标进行插值。比如:做地图投影转换,对目标图像的一个象素进行坐标变换到源图像上对应的点时,变换出来的对应的坐标是一个小数,再比如做图像的几何校正,也会碰到同样的问题。以下是对常用的三种数字图像插值方法进行介绍。
1、最邻近元法
这是最简单的一种插值方法,不需要计算,在待求象素的四邻象素中,将距离待求象素最近的邻象素灰度赋给待求象素。设i+u,j+v(i, j为正整数, u, v为大于零小于1的小数,下同)为待求象素坐标,则待求象素灰度的值 f(i+u,j+v) 如下图所示:
如果(i+u, j+v)落在A区,即u<0.5,v<0.5,则将左上角象素的灰度值赋给待求象素,同理,落在B区则赋予右上角的象素灰度值,落在C区则赋予左下角象素的灰度值,落在D区则赋予右下角象素的灰度值。
最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
2、双线性内插法
双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插,如下图所示:
对于 (i, j+v),f(i, j) 到 f(i, j+1)的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] *v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1,j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v)的灰度变化也为线性关系,由此可推导出待求象素灰度的计算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u *(1-v) * f(i+1, j) + u * v * f(i+1, j+1)
双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
3、三次内插法
该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x,其数学表达式为:
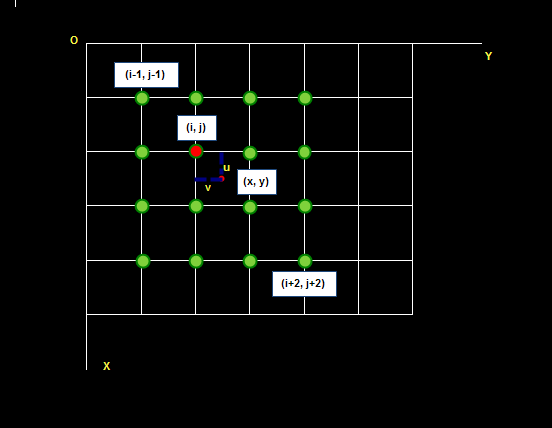
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到,如下图:
待求像素的灰度计算式如下:
f(x, y) = f(i+u, j+v) =ABC
其中:
三次曲线插值方法计算量较大,但插值后的图像效果最好。
第二部分:图像缩放--OpenCVcvResize函数--最近邻插值---双线性插值--基本原理
图像大小变换
void cvResize( const CvArr* src,CvArr* dst, int interpolation=CV_INTER_LINEAR ); src输入图像.dst输出图像.interpolation插值方法:
- CV_INTER_NN - 最近邻插值,
- CV_INTER_LINEAR - 双线性插值 (缺省使用)
- CV_INTER_AREA - 使用象素关系重采样。当图像缩小时候,该方法可以避免波纹出现。当图像放大时,类似于CV_INTER_NN 方法..
- CV_INTER_CUBIC - 立方插值.
函数 cvResize 将图像 src 改变尺寸得到与dst 同样大小。若设定 ROI,函数将按常规支持 ROI.
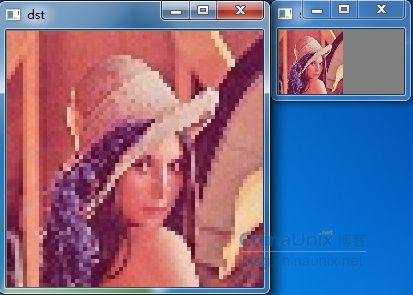
最近邻插值:效果(放大4倍)有马赛克现象
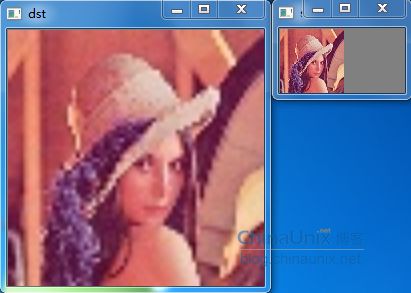
双线性插值:效果(放大4倍)比最近邻插值效果好
最近邻插值和双线性插值的基本原理
图像的缩放很好理解,就是图像的放大和缩小。传统的绘画工具中,有一种叫做“放大尺”的绘画工具,画家常用它来放大图画。当然,在计算机上,我们不再需要用放大尺去放大或缩小图像了,把这个工作交给程序来完成就可以了。下面就来讲讲计算机怎么来放大缩小图象;在本文中,我们所说的图像都是指点阵图,也就是用一个像素矩阵来描述图像的方法,对于另一种图像:用函数来描述图像的矢量图,不在本文讨论之列。
越是简单的模型越适合用来举例子,我们就举个简单的图像:3X3的256级灰度图,也就是高为3个象素,宽也是3个象素的图像,每个象素的取值可以是0-255,代表该像素的亮度,255代表最亮,也就是白色,0代表最暗,即黑色。假如图像的象素矩阵如下图所示(这个原始图把它叫做源图,Source):
234 38 22
67 44 12
89 65 63
这个矩阵中,元素坐标(x,y)是这样确定的,x从左到右,从0开始,y从上到下,也是从零开始,这是图象处理中最常用的坐标系,就是这样一个坐标:
---------------------->X
|
|
|
|
|
∨Y
如果想把这副图放大为4X4大小的图像,那么该怎么做呢?那么第一步肯定想到的是先把4X4的矩阵先画出来再说,好了矩阵画出来了,如下所示,当然,矩阵的每个像素都是未知数,等待着我们去填充(这个将要被填充的图的叫做目标图,Destination):
? ? ? ?
? ? ? ?
? ? ? ?
? ? ? ?
然后要往这个空的矩阵里面填值了,要填的值从哪里来来呢?是从源图中来,好,先填写目标图最左上角的象素,坐标为(0,0),那么该坐标对应源图中的坐标可以由如下公式得出:
srcX=dstX* (srcWidth/dstWidth) , srcY = dstY *(srcHeight/dstHeight)
好了,套用公式,就可以找到对应的原图的坐标了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0)
,找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。
接下来,如法炮制,寻找目标图中坐标为(1,0)的象素对应源图中的坐标,套用公式:
(1*0.75,0*0.75)=>(0.75,0)
结果发现,得到的坐标里面竟然有小数,这可怎么办?计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法(也可以采用直接舍掉小数位的方法),把非整数坐标转换成整数,好,那么按照四舍五入的方法就得到坐标(1,0),完整的运算过程就是这样的:
(1*0.75,0*0.75)=>(0.75,0)=>(1,0)
那么就可以再填一个象素到目标矩阵中了,同样是把源图中坐标为(1,0)处的像素值38填入目标图中的坐标。
依次填完每个象素,一幅放大后的图像就诞生了,像素矩阵如下所示:
234 38 22 22
67 44 12 12
89 65 63 63
89 65 63 63
这种放大图像的方法叫做最临近插值算法,这是一种最基本、最简单的图像缩放算法,效果也是最不好的,放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真;效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真,比如,当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,当推得坐标值为0.75的时候,不应该就简单的取为1,既然是0.75,比1要小0.25 ,比0要大0.75,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的,这样才能达到更好的缩放效果。双线型内插值算法就是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多。
双线性内插值算法描述如下:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v)(其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素得值 f(i+u,j+v)可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) +uvf(i+1,j+1) 公式1
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
比如,象刚才的例子,现在假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75 , 0.75),这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点。
原理参考link:http://blog.csdn.net/andrew659/article/details/4818988
OpenCV代码:scale是放缩比例
点击(此处)折叠或打开
- #include "stdafx.h"
- #include <cv.h>
- #include <cxcore.h>
- #include <highgui.h>
- #include <cmath>
- using namespace std;
- using namespace cv;
- int main(intargc ,char **argv)
- {
- IplImage*scr=0;
- IplImage*dst=0;
- doublescale=4;
- CvSizedst_cvsize;
- if(argc==2&&(scr=cvLoadImage(argv[1],-1))!=0)
- {
- dst_cvsize.width=(int)(scr->width*scale);
- dst_cvsize.height=(int)(scr->height*scale);
- dst=cvCreateImage(dst_cvsize,scr->depth,scr->nChannels);
- cvResize(scr,dst,CV_INTER_NN);//
- // CV_INTER_NN- 最近邻插值,
- // CV_INTER_LINEAR- 双线性插值 (缺省使用)
- // CV_INTER_AREA-使用象素关系重采样。当图像缩小时候,该方法可以避免波纹出现。
- /*当图像放大时,类似于 CV_INTER_NN 方法..*/
- // CV_INTER_CUBIC- 立方插值.
- cvNamedWindow("scr",CV_WINDOW_AUTOSIZE);
- cvNamedWindow("dst",CV_WINDOW_AUTOSIZE);
- cvShowImage("scr",scr);
- cvShowImage("dst",dst);
- cvWaitKey();
- cvReleaseImage(&scr);
- cvReleaseImage(&dst);
- cvDestroyWindow("scr");
- cvDestroyWindow("dst");
- }
- return0;
- }