线性回归学习笔记

线性回归

线性回归

线性模型就是通过属性的线性组合来进行预测的函数：

f(x)=ω1x1+ω2x2+...+ωdxd+b

用向量形式可以写成：

f(x)=ωTx+b

当我们学到参数 ω,b 就可以确定模型。
因此对于 线性回归方法，其目的就是要在一组带标记的数据中学得一个线性模型使得该模型可以更准确的去预测实值输出标记。这里我们假设拥有n个样本 D={(x(1),y(1)),(x(2),y(2)),...,(x(n),y(n))} ，每个样本拥有m个属性 x={x1,x2,...,xm} ，那么线性回归的目标就是尽可能的让我们所学习的线性模型所预测的值 f(x(i)) 与真实标记 y(i) 接近。因为各个特征（属性）都是已知的，因此对于模型的学习实际上就是对参数 (ω,b) 的学习。而对于参数学习的关键又在于对函数 f(x) 和 y 之间差别的衡量，对于回归任务，最常用的性能度量方式就是均方误差。因此我们的目标就是让均方误差最小化：

minE(ω,b)=min12n∑i=1n(f(x(i))−y(i))2=min12n∑i=1n(ωTx(i)+b−y(i))2

因为我们要对n个样本进行运算，因此我们可以将数据转换为矩阵表达方式，即令 W=(ω,b) 为一个 m+1 维的向量，而 X 为一个 n×(m+1) 维的矩阵，其中最后一列元素全为1。因此均方误差最小化可以表达为

minE(W)=min(XW−Y)T(XW−Y)

这种基于均方误差最小化来进行模型求解的方法称为 最小二乘法。 在线性回归中，最小二乘法就是试图找到一条直线，使得所有点到这条直线的距离之和最短。而求解参数的过程称为线性回归模型的 最小二乘参数估计。最优参数的闭式解可以通过对参数进行求导并令其为0得到：

δEδW=δ(WTXTXW−WTXTY−YTXW−YTY)δW=2XT(XW−Y)

令 δEδW=0 有

2XT(XW−Y)=0⇒W∗=(XTX)−1XTY

上面的最优解存在以下两个问题：
1. 当矩阵 XTX 不可逆的时候，其最优解将会有多组；
2. 当数据集非常大的时候，即使可逆，其逆的求解也是非常耗时
对于第一个问题，由于多组解都可以使得均方差最小，因此选择哪个解由模型的偏好来决定，常用的方法是引入正则化项。对于第二个问题，当数据集非常大的时候，一般使用迭代的方法来求解最优解。常用的迭代方法有 梯度下降法， 牛顿法和拟牛顿法。

广义线性回归

假设输出标记并不是在线性尺度上变化，而是在其他更复杂的尺度上变化的时候，可以定义广义线性模型：

y=g−1(ωtx+b)

其中，函数 g(⋅) 为 联系函数，其必须为单调可微的，单调是因为要保证其反函数的存在，而可维则是因为在求最优解的时候要求其导数。

逻辑回归

当我们考虑二分类问题的时候，其输出标记不再是在线性尺度上变化，而是 (0,1) 的离散值，此时我们可以将联系函数定义为单位阶跃函数
y =

⎧⎩⎨0,0.5,1,z<0;z=0;z>0,

来将预测值映射到真实标记所在空间。但是单位阶跃函数并不是连续的，因此其在不连续点不可导，其不能作为联系函数。故我们需要一个单调连续的函数来接近于单位阶跃函数， sigmoid函数就具有这样的特性，如下图所示

我们可以看到sigmoid函数与单位阶跃函数非常的形似，而且是连续函数。该函数的函数表达式为：

y=11+e−z

该函数不仅连续可导，而且可以求任意阶导数，其导数形式也非常的好看 y′=y(1−y) ，故sigmoid函数具有很好的数学特性。那么我们的预测函数就可以写成：

f(x)=11+e−(ωTx+b)

我们可以把该式变化为如下格式：

lnf(x)1−f(x)=ωTx+b

其中 f(x) 视为样本 x 为正例的概率， 1−f(x) 视为样本 x 为反例的概率，两者的比值 f(x)1−f(x) 称为 几率，反映了样本 x 作为正例的相对可能性。
对于参数 (ω,b) ，我们可以使用最大似然估计来进行计算，其中对数似然函数为

L(ω,b)=∑i=1nlnp(f(xi)|x(i);ω,b)

该似然函数的目标就是对每个样本的预测都尽可能的与其真实标记相同。又对样本进行正确预测的概率可以写成：

p(f(xi)|x(i);ω,b)=yip(f(xi)=1|x(i);ω,b)+(1−yi)p(f(xi)=0|x(i);ω,b)

因此，原对数似然函数可以写成：

L(ω,b)=∑i=1nyilnp(f(xi)=1|x(i);ω,b)+(1−yi)lnp(f(xi)=0|x(i);ω,b)=yilnp(f(xi)=1|x(i);ω,b)p(f(xi)=0|x(i);ω,b)+lnp(f(xi)=0|x(i);ω,b)=yi(ωT+b)−ln(1+eωTx+b)

然后我们可以使用梯度下降或者牛顿法来迭代求出最优解

多分类问题

对于多分类问题，通常是将其转换成多个二分类问题来解决的，最常用的三种利用二分类解决多分类问题的策略是：

1.一对一(OVO)：将这N个类别两两配对，从而产生 N(N−1)/2 个二分类器。对于提交的测试集，因为我们拥有 N(N−1)/2 个分类器，因此会产生 N(N−1)/2 个预测结果，最终结果通过投票产生，即把预测的最多的类别作为最终的分类结果；
2.一对其余(OVR)：在一对其余的策略中，我们只把当前类别作为正例，其余的都作为反例来进行训练，这样我们可以得到N个分类器。对于提交的测试集，会得到N个预测结果，如果有多个预测结果为正例，则选择分类器预测置信度最大的类别作为最终类别；
3. 多对多(MVM)：在多对多的策略中，通常将多个类别作为正例，其余的作为反例来进行训练的。其中最常用的多对多技术是输入纠错码（ECOC）。利用该技术进行训练预测通常分为两步：

• 编码：对N个类别进行M次划分，每次划分都是讲一部分类别划分为正例，另一部分划分为反例，从而形成一个二分类器，这样一共可以产生M个二分类器；
• 解码：M个分类器分别对测试样本进行预测，预测的结果可以组成一个编码。将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。

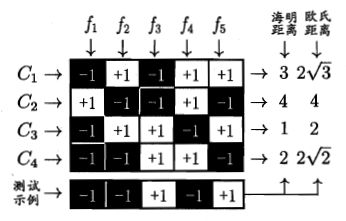
因为我们有M个分类器，因此对于类别 C1,C2，...,CN 都有一个长度为M的编码，其中类别 Cj 编码的第i位是第i个分类器对于类别 Cj 的预测结果，测试集也同样会拥有一个长度为M的编码，如下图所示：

类别不平衡问题

在前面对各种算法的描述中，我们都假设类别是平衡的，即各个类别在样本集中所占的比例是差不多的。但是在实际情况中，很容易发生类别不平衡的问题，即类别在样本集中差别很大。假设在某个数据集中正例有99个，而反例则只有1个，那么训练得到的模型只需要把所有新来的数据都预测为正，就可以达到99%的正确率，但是这样的模型是完全没有意义的，其无法预测出任何的反例。
对于类别不平衡问题通常有三种基本的方法来处理：

1. 欠采样：去除一些样本类别占比大的样本使得各个类别的占比接近，然后再进行学习。但是如果只是简单地丢掉一些样例，可能导致重要信息的丢失，因此通常会使用类似集成学习机制，将占比大的类别分为若干个集合供不同学习器使用，这样对于每个学习器都相当于进行了欠采样，但全局来看并没有丢失重要信息；
2. 过采样：增加一些样本类别占比小的样本使得各个类别的占比接近，然后再进行学习。增加占比小的类别样本并不是简单的对原有正例进行重复采样（因为其会导致过拟合），而是对训练集中的正例进行插值从而产生额外的正例；
3. 阈值移动：通常我们利用逻辑回归模型对某个样本进行预测的时候，会首先计算该样本为正例的概率值，然后将该概率值与某个阈值进行比较，如果其大于阈值，则为正例，反之为反例。假设我们设阈值为0.5，那么用几率来描述就是当 y1−y>1 时表示为正例的概率要大于0.5，此时我们可以把样本预测为正例。因此我们也可以用几率来作为分类决策器。通常我们设阈值为0.5，此时我们用该阈值的时候，相当于默认了在样本集中，正例样本与反例样本可能性相同。但是通常我们的样本是不平衡的，有偏的。令 m+ 为训练集中正例样本数， m− 为训练集中反例样本数，那么观察几率就为 m+m− ，假设训练集是真实样本集无偏采样，那么观测几率就可以代表真实几率，那么此时观测决策函数应该变为 y1−y×m−m+ 是否大于1，如果大于则说明是正例。因为 y1−y×m−m+>1⇒y1−y>m+m− ，因此其相当于对阈值进行了移动，故称为阈值移动方法。但是由于训练集是真实样本集的无偏采样这个假设很难保证，因此此方法也值得商榷。