数独生成求解器——软件工程2018年个人作业项目（完成）

最近更新时间2018.12.29（百忙之中实现了UI界面，另开了一篇）

GitHub连接：https://github.com/blingopen/sudoku

部分参考资料链接（有些参考之后忘记贴出来了）：

• Git和Github使用
• C#读写文件
• 模板法生成数独
• 回溯法生成数独
• 解决Random函数随机数重复
• 在线画概要设计图网站

内容目录

需求分析

概要设计

详细设计&核心代码实现

求解数独算法

生成终局函数

随机函数（生成随机数组）

输入输出函数

主函数

改进与提升！

性能分析与提高

单元测试

Sudoku类内测试

主函数测试

代码质量分析

        总结

---

 

---

此软件会用C#语言编写。 

首先我对这个数独项目完成的时间做了一个大致的估计。

psp2.1表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60
·Estimate	·估计这个任务需要多少时间	60
Development	开发	1170
· Analysis	· 需求分析（包括学习新技术）	300
· Design Spec	· 生成设计文档	30
· Design Review	· 设计复审（和同事审核设计文档）	0
· Coding Standard	· 代码规范（为目前的开发制定合适的规范）	60
· Design	· 具体设计	180
· Coding	· 具体编码	300
· Coding Review	· 代码复审	120
· Test	· 测试（自我测试，修改代码，提交修改）	180
Reporting	报告	360
· Test Reporting	· 测试报告	120
· Size Measurement	· 计算工作量	60
· Postmortem & Process Improvement Plan	· 事后总结，并提出过程改进计划	180
	合计	1590

本项目为个人项目，所以设计复审为本人自行复审（算在需求分析中），故和同行设计复审一栏时间花费为0.

需求分析

拿到题目之后我读了好几遍，终于把这个数独的需求摸索清楚了：

1. 在控制台输入指令“sudoku.exe -c 有效数字”可以输出改有效数字数量的数独终局到txt文件中。
2. 在控制台输入“sudoku.exe -s 绝对路径”可以读取绝对路径中txt文本中的数独，求解并输出结果到txt文件中。

首先计划了一番，计划的大致时间如上表，因为需求比较明确，并且功能没有很复杂，所以准备用瀑布模型来开发。

接着，我思考了一下，程序结构很简单，主要可分为以下几个板块，区分指令板块（包括不同的有效指令和无效指令），生成多个数独终局板块，求解数独板块，第一个板块直接在主函数中写一个判断就可以，后面两个板块要分别设计一些算法。

当然设计算法是后话，“工欲善其事，必先利其器”，要先把准备工作做好。所以先按照文档要求，创建一个CSDN博客和GitHub工程文件夹，在这里寻求百度的帮助，查找了一些使用GitHub和Git的方法，配置好了相关环境，建立了相应的文件夹和博客。（前三次commit是试验自己是否创建成功）

然后按照正常的瀑布模型开发流程，计划了大致时间后，写了一个需求分析，参考了网上的模板和教材的流程，存入了GitHub中（文件 Analysis.docx），其中建模结果大致如下。

 

数据建模

             本软件数据较为简单，抽象出来的实体只有一个完整的9×9的数独，和对应的每个3×3的小矩阵（共9个）。

图 1 sudoku系统初步ER图

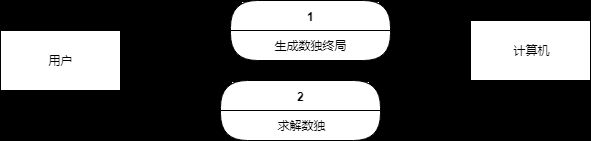
功能建模

            数据源即用户，数据终点为本地计算机，主要数据流即用户在控制台应用输入的各种指令和输出结果，主要处理过程即生成终局和求解数独。（详细设计回来发现此处图有些不恰当）

图 2 sudoku系统顶层DFD图

            继续划分，系统主要分为数独生成终局部分和数度求解部分，无法进一步精细化，故画到一层即可。

图 3 sudoku系统第1层DFD图

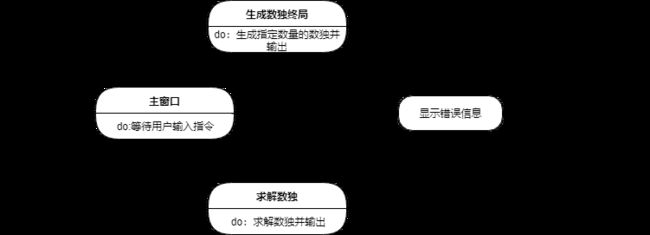
行为建模

          主要状态分为等待指令的主界面状态，生成终局状态，求解数独状态和错误信息状态，其行为关系如下：（详细设计回来发现此处图有些不恰当）

图 4 sudoku系统的状态图

通读文档需要学习的新技术有：

1. 使用GitHub和git来管理代码。
2. 生成数独终局和数独求解的算法。
3. 如何使用代码质量分析工具，性能分析和诊断工具。
4. 如何写GUI。

在之后的相应步骤处会仔细说明如何查找材料与具体步骤。接下来是设计阶段。（对应文档HighLevelDesign.docx）

概要设计

关于类的设计，需求分析中大概设计了两个类，后来觉得设置一个类应该就可以了，3×3矩阵的判断可以转化成一个二维数组。便于判定每个3×3矩阵内内行每列是否满足1-9只出现了一次，所以就除了本身的数独数组，分别设置了3个判定数组。

该类命名为Sudoku类，包含四个字段及其相应属性分别是：

字段	属性	类型	含义
shudu	Shudu	Char [9,9]数组 int[9,9]数组	数独矩阵
hang	Hang	Bool [9,9]数组	行判定，每一行代表数独每一行，从上至下依次标号，每一列代表数独该行该数是否出现
lie	Lie	Bool [9,9]数组	列判定，每一行代表数独每一列，从左至右依次标号，每一列代表数独该列该数是否出现
sansan	Sansan	Bool [9,9]数组	行判定，每一行代表数独每一个3*3小矩阵，从左至右从上至下依次标号，每一列代表数独该小矩阵该数是否出现

包含两个函数分别是public void GenerateSudokuEnding（）和public void SolveSudoku（），分别用来生成终局和求解数独。

两个函数之间没有直接关联，是两种关于数独的功能（详细设计发现还是有调用关系的），不过内部会调用相关的字段，比如判断改行是否有重复数字的时候会查看hang，lie，sansan数组，同时会将数字写入shudu数组。

Sudoku类的数据结构大致如图所示：（以下类仅仅是概要设计，还不完全）

class Sudoku
    {
        public void GenerateSudokuEnding()
        {
           //填充部分
        }
        public void SovleSudoku()
        {
            //填充部分
        }
        private char[,] shudu = new char[9, 9];//数独矩阵
        public char[,] Shudu
        {
            get { return shudu; }
            set { shudu = value; }
        }
        private bool[,] hang = new bool[9, 9];//行检验矩阵
        public bool[,] Hang
        {
            get { return hang; }
            set { hang = value; }
        }
        private bool[,] lie = new bool[9, 9];//列检验矩阵
        public bool[,] Lie
        {
            get { return lie; }
            set { lie = value; }
        }
        private bool[,] sansan = new bool[9, 9];//3×3检验矩阵
        public bool[,] Sansan
        {
            get { return sansan; }
            set { sansan = value; }
        }
     }
}

软件主操作界面为控制台，所有的参数输入都通过控制台传输给主函数，由主函数来判断具体的命令操作（同时也会判断命令是否正确），根据不同命令参数去执行不同板块：

1. 在控制台输入指令“sudoku.exe -c 有效数字”可以输出改有效数字数量的数独终局到txt文件中。
2. 输入“sudoku.exe -s 绝对路径”可以读取绝对路径中txt文本中的数独，求解并输出结果

当判断为命令1时，会调用Sudoku类的GenerateSudokuEnding函数来生成数独；当命令为2时，会调用Sudoku类的SolveSudoku函数来求解，否则，判定为无效命令，结束程序。

同时设置了一个输出函数static void OutputToTxt(Sudoku sudoku,StreamWriter streamWriter)，统一将生成的数独输出到TXT文件中。

此时，程序的大体框架就构建出来了，接下来就是细化各个模块函数需要实现的算法，算法详细设计。

详细设计&核心代码实现

为了方便处理，把数独数组的char型改成了int型（对应文档LowLevelDesign.docx）

求解数独算法

最开始的想法无论是求解数独还是生成终局，全部暴力+回溯，但是在1e6的大数量情况下显然会很慢。

经过思考，想了想还是用递归，不过要大量剪枝，先做预处理。给Sudoku类加了三个数组分别是hang[9,9]，lie[9,9]，sansan[9,9]，即牺牲内存来换时间，第一个参数分别代表了第i行，第i列，第i个小3×3矩阵，第二个参数代表这行出现的数字，如果出现则标记为true，没有出现则标记false，这个方法极大地缩短了时间。

经典的回溯故不详细赘述，以下是代码：

public bool SolveSudoku(int position)
        {
            int index = position;
            for (; index < 81 && 0 != shudu[index / 9, index % 9]; index++) ;//非零就不做

            if (index < 81)
            {
                int line = index / 9;
                int col = index % 9;
                for (int i = 1; i < 10; i++)
                {
                    if (hang[line, i - 1] || lie[col, i - 1] || sansan[line / 3 * 3 + col / 3, i - 1])
                        continue;

                    shudu[line, col] = i;
                    hang[line, i - 1] = true;
                    lie[col, i - 1] = true;
                    sansan[line / 3 * 3 + col / 3, i - 1] = true;

                    if (SolveSudoku(index + 1))
                        return true;

                    shudu[line, col] = 0;
                    hang[line, i - 1] = false;
                    lie[col, i - 1] = false;
                    sansan[line / 3 * 3 + col / 3, i - 1] = false;
                }
                return false;
            }
            return true;
        }

生成终局函数

最开始想暴力+回溯，外面再套一个大循环，显然在1e6的大数量情况下会很慢。

在网上搜索了很多的数独相关资料，发现最快的是模板法，即生成某一行或某一列或某个3*3小矩阵填入模板，即可构成一个完整的数独终局，由于左上角的数字固定为后两位模9+1（我的是（3+5）mod 9 + 1 =9），故共有8！= 40320种，另外23行（第一行固定不动），456行，789行也可互相交换，数独性质仍成立，故一共有40320 × 2！× 3！× 3！约等于3e6，超过了要求的1e6。

这个需要写一个全排列函数，C++有直接的函数可以调用，考虑到C#没有，而且如果之后做UI（学期内应该是没有时间做了）可以游玩，这种方法生成的数独矩阵很固定可玩性不高，于是想到了生成随机数，思路又回归到了回溯法上。

先思考我们也可以实现填上一部分数字，然后用回溯方法，这里可以调用求解数独的函数。一共有9个3×3矩阵，对角线上的3个矩阵是互不干扰的，所以可以随机生成这三个矩阵，然后用优化后的回溯来生成数独解，回溯方法生成的是固定解，所以种子相同，解就会相同，所以这种方法原则上可以生成8！× 9！× 9！约等于1e15，所以添加一个随机函数来打乱1-9的数组填进去就可以了，应该会有重复的情况，推测重复的概率会非常小。同时，每次生成完一个终局后要初始化Sudoku类的对象，重置预处理的标记等。

首先是生成3*3小矩阵的代码，由于第一个矩阵第一个数字不能动，所以将1与5，9区别开来，考虑到分开写两个函数重复度很大，故将其重构成一个函数，用标号加以区分，首先调用void Program.Random159（int[]）函数生成随机数组，然后将数字填进去，并且预处理。

 private void Generate33(int[] gene, int num)
        {
            int temp = 0;
            int row;
            switch (num)
            {
                case 1: { row = 1; temp = 1; } break;
                case 5: row = 4; break;
                default: row = 7; break;
            }
            Program.Random159(gene);//调用生成随机数组的函数
            for (int i = 0; i < gene.Length; i++)
            {
                if (i + temp < 3)
                {
                    shudu[row - 1, row / 3 * 3 + (i + temp) % 3] = gene[i];
                    hang[row - 1, gene[i] - 1] = true;
                }
                else if (i + temp < 6)
                {
                    shudu[row, row / 3 * 3 + (i + temp) % 3] = gene[i];
                    hang[row, gene[i] - 1] = true;
                }
                else
                {
                    shudu[row + 1, row / 3 * 3 + (i + temp) % 3] = gene[i];
                    hang[row + 1, gene[i] - 1] = true;
                }

                lie[row / 3 * 3 + (i + temp) % 3, gene[i] - 1] = true;
                sansan[num - 1, gene[i] - 1] = true;
            }
        }

然后是数独终局生成函数，基本上是在调用其他函数。

 public void GenerateSudokuEnding()
        {
            int[] gene59 = new int[9] { 9,5,2,7,6,1,3,8,4 };//5,9矩阵的种子数组
            int[] gene1 = new int[8] { 5,2,7,3,6,8,1,4 };//1矩阵的种子数组
            Generate33(gene1, 1);
            Generate33(gene59, 5);
            Generate33(gene59, 9);
            SolveSudoku(0);//调用递归
        }

每次重新生成一个新的数独终局之前，都要将数独初始化，除了第一个位置为固定数字外，其余的均为0，并且预处理的数组也相应初始化。

public void Initialize()
        {
            for (int i = 0; i < 9; i++)
            {
                for (int j = 0; j < 9; j++)
                {
                    shudu[i, j] = 0;
                    hang[i, j] = false;
                    lie[i, j] = false;
                    sansan[i, j] = false;
                }
            }
            shudu[0, 0] = 9;
            hang[0, 9 - 1] = true;
            lie[0, 9 - 1] = true;
            sansan[0, 9 - 1] = true;
        }

还是有些打脸，之前说两个函数彼此之间应该是独立的，然而最终变成了一个调用另一个，所以需求分析中画的功能（图2,3）和行为建模图（图4）不是很准确了。 

 

随机函数（生成随机数组）

手动写了一个打乱数组的算法，即在当前数组号中随机抽一个，把该位置的元素与末尾元素交换，当前数组号减1，重复上述步骤直到数组号为1，因为用不到Sudoku类内的元素，所以写在了主函数类中。

public static void Random159(int[] gene)
        {
            Random rand = new Random();
            for (int i = gene.Length - 1; i > 0; i--)
            {
                int rdmchar = rand.Next(1000) % i;
                int temp = gene[rdmchar];
                gene[rdmchar] = gene[i];
                gene[i] = temp;
            }
        }

输入输出函数

用的是普通的流读写，很简单的文件操作，就不贴代码了，值得注意的是输出文件要输出到相对路径文件夹，所以调用了一个系统函数：

System.AppDomain.CurrentDomain.BaseDirectory

 这个函数会记录当前应用程序的所在文件夹路径，并返回该路径的字符串，所以生成输出文件的地址也就很方便了。

主函数

主控模块（Main）主要用来接收参数并判断命令。

控制台接收命令参数，主要从args这个字符串数组传入，以空格分割，一个参数存入一个单元，由于两个命令都是双目操作，所以数组长度如果不等于2则判断命令有误。

当命令为-c 时，第二个参数我们试图将其变为整型，如果合法则调用生成数独函数，生成终局写入txt文件中，不合法则报错。

当命令为-s 时，第二个参数我们先检验书读文件绝对路径是否存在，如果存在则按行读取直到文件尾，读入的数据存入到一个string中，再按空格进行分割到string数组中，然后每81个构成一个数独谜题求解输出，直到将所有的数字用完，否则报错。

由于只有两个命令所以判断都写在了主函数中，日后有时间可以进行重构，使代码看起来清晰美观，若增加命令也可复用。主函数看起来比较乱，所以不在此贴代码，可以去GitHub中查看。

改进与提升！

输出发现有一些数独连续几个是完全相同的，查找了很多原因都没能解决，最终找到了问题的根本原因——随机函数有周期。

通过查资料了解到，所有的随机函数都是伪随机函数，默认的Random是以时间为种子的，短时间内生成的随机数是相同的（这也就解释了写完发现有好几个终局是连续相同的），后来查到了一个延时的算法来上随机函数的种子刷新，random之前加入了sleep函数，效果还算可以，但也正是因为延时，所以时间变得很慢。

Thread.Sleep(1);//被弃用的延时

后来查到了一个获得随机数的办法，用一个加密算法生成一串比特位，然后将这个比特位转换成整型数作为种子即可。

这个方法生成的终局目前来看没有重复的，比较高效。

static int GetRandomSeed()
        {
            byte[] bytes = new byte[10];
            System.Security.Cryptography.RNGCryptoServiceProvider rng = new System.Security.Cryptography.RNGCryptoServiceProvider();
            rng.GetBytes(bytes);
            return BitConverter.ToInt32(bytes, 0);
        }

随机函数的生成对象也应改为：

Random rand = new Random(GetRandomSeed());

代码基本完毕，操作系统考试后继续更新，单元测试，代码分析等。

性能分析与提高

图5 性能分析1

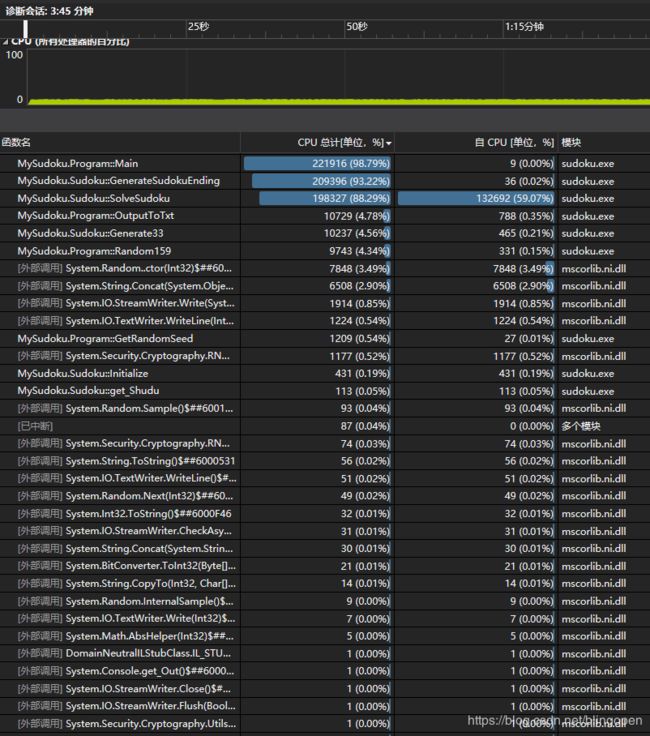
可以看出，主要是SolveSudoku（）函数耗时最多，点进去可以看出，递归调用最红（消耗最多），即回溯法生成数独终局的方法很慢，整体生成1e6个终局用时大致会在3-4分钟。 

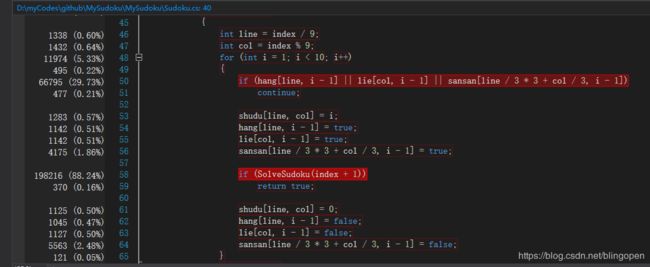標图6 耗资源最多的函数

虽然之前说不用模板法，但最终还是要向模板法低头（真香！），所以我要重新写一个生成终局的函数，用模板法，由于没有内置全排列函数，只能自己写递归来生成，由上面可知递归很耗时间，所以我们要尽可能少的进行递归调用，由之前的计算结果，一个模板，可以经过行变换（第一行不动），生成72个不同的终局，所以我们最多会需要用到1000000/72+1=13889个全排列种子，而不必生成全部全排列（8！=40320个），大大降低了递归的使用。

更改这一部分代码进行了部分重构以及修改，相对麻烦，大概耗费了我3个小时的时间。

 以下是递归生成全排列的函数：

public static int[,] pailie = new int[13890, 8];//存入所有生成的排列
public static int row = 0;//记录排列的行数
static int count = 0;//记录生成了多少个排列，便于跳出递归
        //nums为需要排列的数组，start为开始位置，length为数组长度，amount为生成排列的数量
        public static void Permutation(int[] nums, int start, int length, int amount)
        {
            int i;
            if (count > amount)
                return;
            else
            {
                if (start < length - 1)
                {
                    Permutation(nums, start + 1, length, amount);
                    if (count > amount)
                        return;
                    for (i = start + 1; i < length; i++)
                    {
                        Swap(nums, start, i);
                        //
                        Permutation(nums, start + 1, length, amount);
                        //
                        if (count > amount)
                            return;
                        Swap(nums, start, i);
                    }
                }
                else
                {
                    count++;
                    for (int j = 0; j < nums.Length; j++)
                    {
                        pailie[row, j] = nums[j];
                    }
                    row++;
                }
            }
        }

​

 预处理函数：

​
public static void Pretreat(int amount)//amount为需要生成终局的数目
        {
            int preamount = amount / 72 + 1;
            int[] nums = new int[] { 1, 2, 3, 4, 5, 6, 7, 8 };
            Permutation(nums, 0, nums.Length, preamount);
        }

​

模板法生成终局的函数写在了Sudoku类中，在网上找到了以下模板进行使用：

图6 数独终局模板

代码如下：

public void GenerateSudokuEnding2(int row)//row为Program.pailie数组的全排列序号
        {
            char[,] model = new char[9, 9] {
                { 'i','g','h','c','a','b','f','d','e' },
                { 'c','a','b','f','d','e','i','g','h' },
                { 'f','d','e','i','g','h','c','a','b' },
                { 'g','h','i','a','b','c','d','e','f' },
                { 'a','b','c','d','e','f','g','h','i' },
                { 'd','e','f','g','h','i','a','b','c' },
                { 'h','i','g','b','c','a','e','f','d' },
                { 'b','c','a','e','f','d','h','i','g' },
                { 'e','f','d','h','i','g','b','c','a' }
            };//模板

            for (int i = 0; i < 9; i++)
            {
                for (int j = 0; j < 9; j++)
                {
                    if (model[i, j] == 'i') shudu[i, j] = 9;
                    else if (model[i, j] == 'g') shudu[i, j] = Program.pailie[row, 0];
                    else if (model[i, j] == 'h') shudu[i, j] = Program.pailie[row, 1];
                    else if (model[i, j] == 'c') shudu[i, j] = Program.pailie[row, 2];
                    else if (model[i, j] == 'a') shudu[i, j] = Program.pailie[row, 3];
                    else if (model[i, j] == 'b') shudu[i, j] = Program.pailie[row, 4];
                    else if (model[i, j] == 'f') shudu[i, j] = Program.pailie[row, 5];
                    else if (model[i, j] == 'd') shudu[i, j] = Program.pailie[row, 6];
                    else if (model[i, j] == 'e') shudu[i, j] = Program.pailie[row, 7];
                }//映射数字
            }
        }

交换的话，写了三个大循环，由外到里分别执行2,6,6次（共2*6*6），里面两层第0次什么也不做，第奇数次（1,3,5）交换三行中的后两行，非零偶数次交换三行中的前两行，为了不破坏数独的结构，交换时我们另开一个数组来记录所有行的顺序，然后按行的顺序来输出而不改变数独矩阵的结构。

​
//该函数直接调用了输出函数。amount为需要生成的终局个数。
static void GeneAndTransAndOut(int amount,Sudoku sudoku,int[] order,StreamWriter streamWriter)
        {
            for (int i = 0; i < row && amount > 0; i++)
            {
                sudoku.GenerateSudokuEnding2(i);
                for (int p = 0; p < 2 && amount > 0; p++)//对1,2行的交换（0行不动）
                {
                    if (p == 0)
                    {

                    }
                    else
                    {
                        Swap(order, 1, 2);
                    }
                    for (int j = 0; j < 6 && amount > 0; j++)//对3,4,5行的交换
                    {
                        if (j == 0)
                        {

                        }
                        else if (j % 2 == 1)
                        {
                            Swap(order, 4, 5);
                        }
                        else
                        {
                            Swap(order, 3, 4);
                        }
                        for (int k = 0; k < 6 && amount > 0; k++)//对6,7,8行的交换
                        {
                            if (k == 0)
                            {

                            }
                            else if (k % 2 == 1)
                            {
                                Swap(order, 7, 8);
                            }
                            else
                            {
                                Swap(order, 6, 7);
                            }

                            OutputToTxt(sudoku.Shudu, order, streamWriter);//输出
                            amount--;
                        }
                    }
                }
            }
        }

​

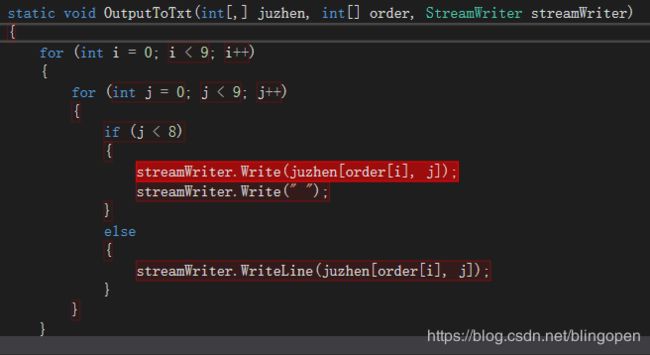
由于改变了输出方式，我们的输出函数也随之改变了传入参数：

static void OutputToTxt(int[,] juzhen, int[] order, StreamWriter streamWriter)
        {
            for (int i = 0; i < 9; i++)
            {
                for (int j = 0; j < 9; j++)
                {
                    if (j < 8)
                    {
                        streamWriter.Write(juzhen[order[i], j]);
                        streamWriter.Write(" ");
                    }
                    else
                    {
                        streamWriter.WriteLine(juzhen[order[i], j]);
                    }
                }
            }
            streamWriter.WriteLine();
        }

 这样，我们重新用代码分析工具来分析一下：

图7 优化后的性能分析图

 

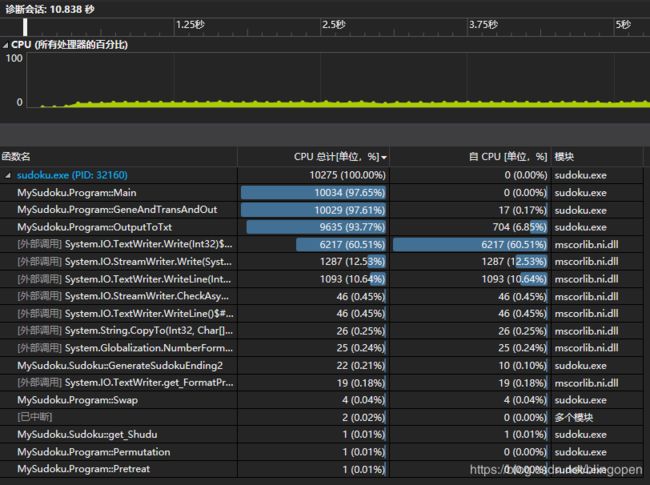
发现大概需要10秒就可以生成1e6的不重复终局！分析后发现，生成终局的代码资源占用较少，可以看到频繁的读写，占用的时间多。

图8 优化后的耗资源的函数

对于读写的优化暂不做处理，但从分钟到秒的计量单位变换，足以说明了优化很成功！

单元测试（对应文档TesCase.xlsx）

Sudoku类内测试

VS内部可直接生成测试类，对于测试类测试用例的设计，每个函数都只生成一个矩阵来检验是否生成正确，由于一部分调用函数和变量写在了类外，测试只能测试Sudoku类内部函数，所以测试类中的测试数据会很奇怪。比如GenerateSudokuEnding2类直接调用的话Program.pailie数组中所有元素都为0，所以测试用例要这样设计：

[TestMethod()]
        public void GenerateSudokuEnding2Test()
        {
            Sudoku sudoku = new Sudoku();
            
            sudoku.GenerateSudokuEnding2(0);
            int[,] ending = new int[9, 9] {{ 9,0,0,0,0,0,0,0,0 },
                                           { 0,0,0,0,0,0,9,0,0 },
                                           { 0,0,0,9,0,0,0,0,0 },
                                           { 0,0,9,0,0,0,0,0,0 },
                                           { 0,0,0,0,0,0,0,0,9 },
                                           { 0,0,0,0,0,9,0,0,0 },
                                           { 0,9,0,0,0,0,0,0,0 },
                                           { 0,0,0,0,0,0,0,9,0 },
                                           { 0,0,0,0,9,0,0,0,0 }
                                            };
            
            for (int i = 0; i < 9; i++)
            {
                for (int j = 0; j < 9; j++)
                {
                    Assert.AreEqual(ending[i,j], sudoku.Shudu[i, j]);
                }
            }
        }

初始化和构造函数的设计相同，即除了第一个数字是9之外，其余的数字均为0。

求解数独函数也是求解一个第一个数字为9，其余的全是空白的数独，由于是回溯法，所以求解结果是固定的。

[TestMethod()]
        public void SolveSudokuTest()
        {
            Sudoku sudoku = new Sudoku();
            sudoku.SolveSudoku(0);
            int[,] ending = new int[9, 9] {{ 9,1,2,3,4,5,6,7,8 },
                                           { 3,4,5,6,7,8,1,2,9 },
                                           { 6,7,8,1,2,9,3,4,5 },
                                           { 1,2,3,4,5,6,8,9,7 },
                                           { 4,5,6,8,9,7,2,1,3 },
                                           { 7,8,9,2,1,3,4,5,6 },
                                           { 2,3,7,5,6,1,9,8,4 },
                                           { 5,6,1,9,8,4,7,3,2 },
                                           { 8,9,4,7,3,2,5,6,1 }
                                            }; 
            for (int i = 0; i < 9; i++)
            {
                for (int j = 0; j < 9; j++)
                {
                    Assert.AreEqual(ending[i, j], sudoku.Shudu[i, j]);
                }
            }
        }

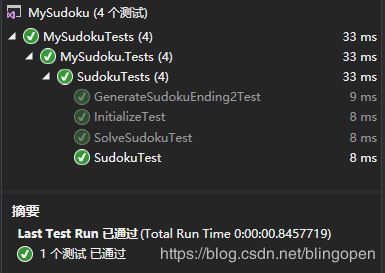
最后运行结果：（没有找到在哪里看覆盖率）

图9 单元测试结果

测试成功。

主函数测试

主函数的测试，由于读入控制台指令的工作在主函数中完成，所以就只能手动在控制台测试，列了一张测试用例表如下：

（从左到右依次是 模块，序号，输入，说明，预期输出，是否测试成功）

图10 主函数测试用例

达到了预期目标。

代码质量分析

此环节选择了StyleCop.Analyzers，对代码风格进行了分析修正。

屏蔽了SA1652规则（与XML有关），最终修正后的代码编译无警告信息。

图10 编译后无警告

总结

终于赶完了这个大作业，学期内应该是做不了UI了，有一些遗憾，不过假期应该会继续把UI部分做出来的。

总的来说，自己还有很多东西要学，设计和编码的能力也都需要提高，整个开发过程都是自己一边查资料一边学习做出来的，感觉做成一个完整的项目实属不易。

总结了一下自己还有许多不足：

1. 当初计划过于笼统，导致时间安排不是很正确，效率不是很高。
2. 概要设计的时候把整个系统想的过于简单，实际实现的过程中发现，有许多细节是之前没有考虑到的。比如开始设计的随机函数在短时间内无法随机的问题。
3. 虽然用的是面向对象语言，但是实际写代码时，封装的不是很好，类内类外的函数互相随便调用，导致耦合性太强，单元测试的时候无法好好测试。
4. 主函数负担过多，可以进一步重构，多弄几个函数增加复用性，不过没时间了。

自己也收获了很多：

1. 学会了如何简单地使用代码分析工具，性能分析工具和单元测试工具。
2. 积累了一点开发软件的经验，对之后的开发心里有了一些B数。
3. 学会了更认真的思考，如何思考如何解决问题。
4. 对编程语言更加熟悉了一些。

psp表格如下：（不知道为啥表格粘贴失败，只好在excel里截图发了）

图11 PSP表格

学无止境，还是要多多加油！